一、说明
在《华尔街的随机漫步》一书中,作者伯顿·马尔基尔(Burton G. Malkiel)声称:“一只蒙着眼睛的猴子向报纸的财经版面投掷飞镖,可以选择一个与专家精心挑选的投资组合一样好的投资组合。
如果我们让巴甫洛夫的狗接受强化学习训练,而不是猴子来选择最佳投资组合策略,会怎么样?在本文中,强化学习 (RL) 是一种机器学习技术,智能体在不确定的环境中学习动作,以最大化其价值。智能体从其操作的结果中学习,而无需使用特定于任务的规则进行显式编程,
任何 RL 算法的目标都是找到价值最大化策略 (π):
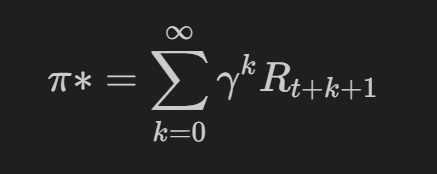
其中 γ (0 ≤ γ ≤ 1) 是控制智能体当前奖励的贴现因子,t 是时间步长,R 是该步骤中的回报。RL 中的策略是在状态 s 中采取措施 a 的概率。
我们将采用的算法是 Q-Learning,这是一种无模型的 RL 算法,旨在通过离散状态的动作的 VALUE 间接学习策略(称为 Q 值),而不是策略本身。它在我们的案例中很有用,因为它不需要对环境进行建模——在我们的案例中,是动荡的资本市场。
估计 Q 值是通过贝尔曼方程完成的:

这些 Q 值被放置在一个详尽的表 (explorarion) 中,并由代理用作查找,以查找当前状态中所有可能操作的 Q 值。从那里,它可以选择具有最高 Q 值(利用)的操作。这在有限的空间内是好的,但在具有无限组合的随机环境中就不行了,我们将用我们的神经网络解决这个问题。
本文中设计的该代理的灵感来自 Théate、Thibaut 和 Ernst, Damien (2021) 的论文。
二、代码和 TPU 要求
本文代码说明,TF Agents Framework、Reverb 和 Gym 需要 Linux 操作系统。如果你和我们一样,喜欢在 VSCode 上工作,请在管理员 powershell 上安装 WSL:wsl — install
更新发行版:sudo apt-get update 和 sudo apt-get install wget ca-certificates。在 WSL cli 中,运行代码 。它将为您打开一个 VSCode。安装 VSCode WSL 扩展以获得无缝的开发人员体验,请参阅此处的教程。
要使用硬件加速,请在 Linux 机器上安装 NVidia 驱动程序。通过以下命令检查安装是否成功:nvidia-smi。安装 TensorFlow 的 cuda 框架:pip install tensorflow[and-cuda] 并验证安装:python3 -c “import tensorflow as tf;print(tf.config.list_physical_devices('GPU'))”
我们准备在GPU或更好的GPU上运行我们的执行策略;通过定义策略,分布在 TPU 中:
if ('COLAB_TPU_ADDR' in os.environ and IN_COLAB) or (IN_KAGGLE and 'TPU_ACCELERATOR_TYPE' in os.environ):
tpu = tf.distribute.cluster_resolver.TPUClusterResolver()
tf.config.experimental_connect_to_cluster(tpu)
tf.tpu.experimental.initialize_tpu_system(tpu)
strategy = tf.distribute.experimental.TPUStrategy(tpu)
print("Running on TPU:", resolver.master())
elif len(tf.config.list_physical_devices('GPU')) > 0:
strategy = tf.distribute.MirroredStrategy()
gpus = tf.config.experimental.list_physical_devices('GPU')
for gpu in gpus:
tf.config.experimental.set_memory_growth(gpu, True)
print("Running on", len(tf.config.list_physical_devices('GPU')), "GPU(s)")
else:
strategy = tf.distribute.get_strategy()
print("Running on CPU")
print("Number of accelerators:", strategy.num_replicas_in_sync)使用 TPU 就绪策略,您可以分配工作负载,例如 BATCH_SIZE = 32 * strategy.num_replicas_in_sync,底层基础设施会将张量分发到 TPU 或 GPU。
注意:TF Agent 的框架在 Kaggle 上对 TPU 的分布式策略存在问题,并在最终迭代中被放弃!
三、财务数据
我们下载了一些财务数据,这现在是我们所有文章的标准。
def get_tickerdata(tickers_symbols, start=START_DATE, end=END_DATE, interval=INTERVAL, datadir=DATA_DIR):
tickers = {}
earliest_end= datetime.strptime(end,'%Y-%m-%d')
latest_start = datetime.strptime(start,'%Y-%m-%d')
os.makedirs(DATA_DIR, exist_ok=True)
for symbol in tickers_symbols:
cached_file_path = f"{datadir}/{symbol}-{start}-{end}-{interval}.csv"
try:
if os.path.exists(cached_file_path):
df = pd.read_parquet(cached_file_path)
df.index = pd.to_datetime(df.index)
assert len(df) > 0
else:
df = yf.download(
symbol,
start=START_DATE,
end=END_DATE,
progress=False,
interval=INTERVAL,
)
assert len(df) > 0
df.to_parquet(cached_file_path, index=True, compression="snappy")
min_date = df.index.min()
max_date = df.index.max()
nan_count = df["Close"].isnull().sum()
skewness = round(skew(df["Close"].dropna()), 2)
kurt = round(kurtosis(df["Close"].dropna()), 2)
outliers_count = (df["Close"] > df["Close"].mean() + (3 * df["Close"].std())).sum()
print(
f"{symbol} => min_date: {min_date}, max_date: {max_date}, kurt:{kurt}, skewness:{skewness}, outliers_count:{outliers_count}, nan_count: {nan_count}"
)
tickers[symbol] = df
if min_date > latest_start:
latest_start = min_date
if max_date < earliest_end:
earliest_end = max_date
except Exception as e:
print(f"Error with {symbol}: {e}")
return tickers, latest_start, earliest_end
tickers, latest_start, earliest_end = get_tickerdata(TICKER_SYMBOLS)
tickers[TARGET]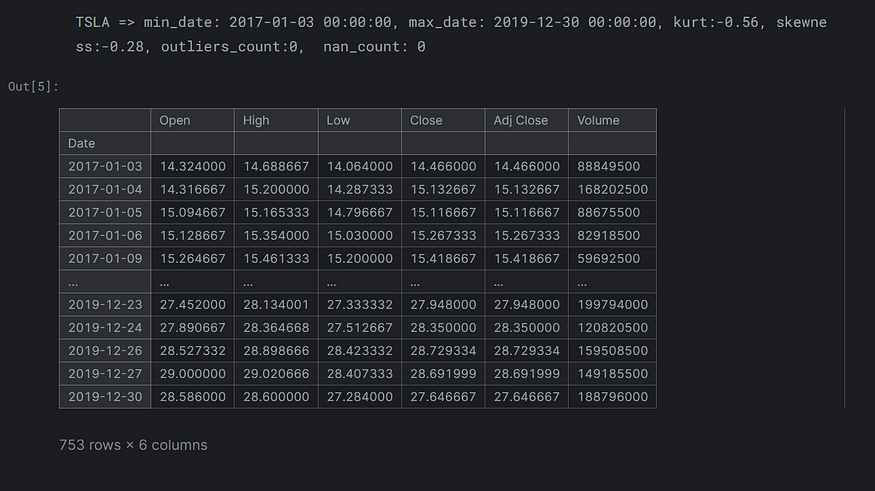
四、问题定义
通过 Q-Training,我们将教巴甫洛夫代理进行交易。我们的目标是进行顺序交互,从而实现最高夏普比,通过该策略形式化(记住 Q-Learning 是非策略的,我们不会直接学习这一点):
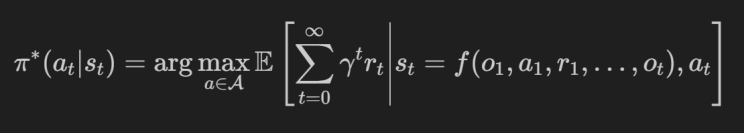
在每个时间步 t:
观察环境状态 st 并使用 f(.) 映射历史记录 来自历史 ht 的观察 ot 具有先前的操作 a_t-1、先前的观察 o_t-1 及其返回 r_t-1。
在我们的实验中,我们将这些编码为网络的特征。
执行动作a_t,可以是:hold、long、short以 γt 获得r_t折扣的退货。γ是防止代理人只为当前回报做出战术选择(错过更好的未来回报)的贴现因素。
π(at|ht) 在 = Qt 处对数量 Q 创建操作。其中正 Q 是多头,负 Q 表示空头,当其 0 时不采取任何行动。在本文中,我们将交替使用策略 π(at|ht) 和 Q 值 Q(at,st) 的定义。
五、观测和状态空间
本文仅使用最高价、最低价、开盘价、收盘价和成交量作为智能体环境状态的观测值。
在后面的实验中,我们将用 3 个技术指标和 3 个宏观经济指标来扩充这个空间:
- MACD 和 APT,来自我们的文章:“动量和回归交易信号分析”
- 每日VIX作为市场波动和恐惧的代表,以及10年期国债作为通货膨胀和利率的代表,来自我们的文章:“具有广泛市场信号条件的时间卷积神经网络”

六、行动和奖励
RL的一个核心概念是奖励工程。让我们看一下时间 t 的动作空间 A:
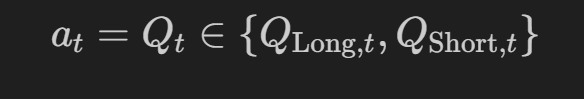
考虑到我们的流动性vc_t(我们投资组合的价值 v,剩余现金 c)和以 p 股的价格购买Q_long(交易成本 C),如果我们还没有做多,则行动 Q_Long,t 旨在最大化买入回报:
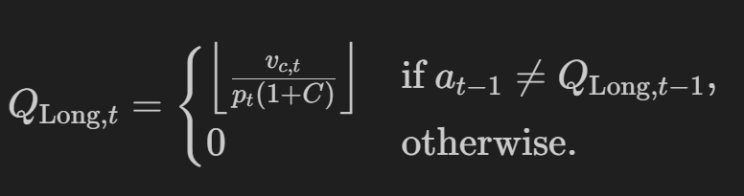
行动 Q_Short,t 旨在将负数的股票转换为回报(做空是借入股票,因此我们的v_c最初将是负数)。

请注意,-2n 表示卖出两次,这意味着不仅要平仓多头头寸,还要为 Qn 股票开立空头头寸,因为做空是一条负轨迹,我们需要否定我们可以买入的金额以获得正确的持仓表示。如果我们没有开始的份额,那么 -2(0) 除了空头金额外,不会产生任何影响:

空头是有风险的,我们需要给代理人设定界限,因为空头可能会招致无限的损失:
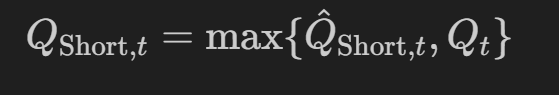
鉴于我们的投资组合不能落入负数,我们需要对约束进行建模。
- 现金价值vc_t需要足够大才能恢复到中性n_t=0。
- 为了回到 0,我们需要调整由市场波动 epsilon ε引起的成本 C(想想滑点、点差等)。
- 我们重新定义了允许的行动空间,以确保我们始终可以恢复到中立状态。

动作空间 A 被重新定义为边界 Q- 和 Q+ 之间的一组可接受的 Q_t值:

其中,顶部边界 Q+ 为:
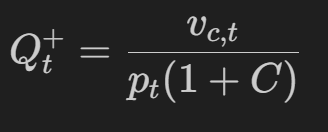
下边界 Q- 是(对于从 delta t 为正的多头出来,或者反转空头并产生两倍的成本,delta t 为负):
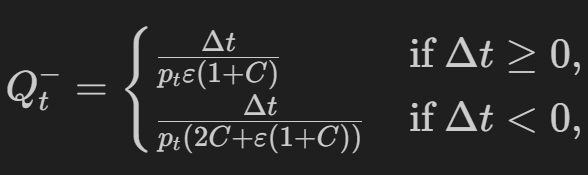
delta t 是投资组合持有价值在时间上的变化:
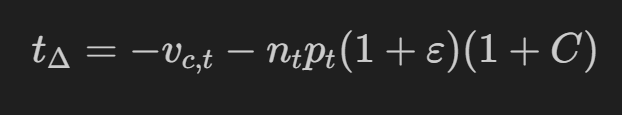
在上述边界中,交易成本定义为:
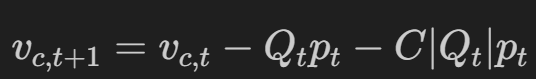
其中 C 是给定绝对数量的事务成本百分比 |Q_t|的股票及其价格p_t。
七、代理目标
在本文中,他们利用百分比回报作为奖励信号,在 -1 和 1 之间剪裁,并通过贴现因子γ进行调整,为代理提供更多战术性的短期奖励:
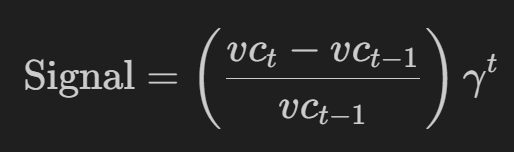
在本文中,我们还将使用年化夏普(从 N 个时间窗口开始,最多 252 个交易日),并教代理生成一个没有贴现因子的最佳比率:
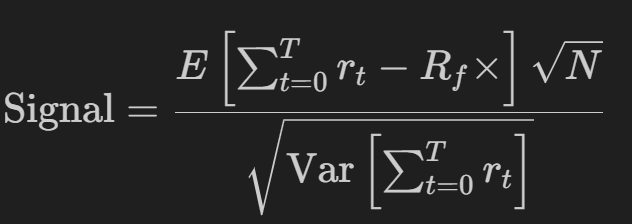
这只是最大化:

或投资组合的回报率(R平均值)减去无风险利率(Rf,在撰写本文时为5%)除以投资组合的波动率(σ)
八、交易环境
使用 TensorFlow 的 PyEnvironment,我们将为代理提供实现上述规则的环境:
class TradingEnv(py_environment.PyEnvironment):
"""
A custom trading environment for reinforcement learning, compatible with tf_agents.
This environment simulates a simple trading scenario where an agent can take one of three actions:
- Long (buy), Short (sell), or Hold a financial instrument, aiming to maximize profit through trading decisions.
Parameters:
- data: DataFrame containing the stock market data.
- data_dim: Dimension of the data to be used for each observation.
- money: Initial capital to start trading.
- state_length: Number of past observations to consider for the state.
- transaction_cost: Costs associated with trading actions.
"""
def __init__(self, data, features = FEATURES, money=CAPITAL, state_length=STATE_LEN, transaction_cost=0, market_costs=TRADE_COSTS_PERCENT, reward_discount=DISCOUNT):
super(TradingEnv, self).__init__()
assert data is not None
self.features = features
self.data_dim = len(self.features)
self.state_length = state_length
self.current_step = self.state_length
self.reward_discount = reward_discount
self.balance = money
self.initial_balance = money
self.transaction_cost = transaction_cost
self.epsilon = max(market_costs, np.finfo(float).eps) # there is always volatility costs
self.total_shares = 0
self._episode_ended = False
self._batch_size = 1
self._action_spec = array_spec.BoundedArraySpec(shape=(), dtype=np.int32, minimum=ACT_SHORT, maximum=ACT_LONG, name='action')
self._observation_spec = array_spec.BoundedArraySpec(shape=(self.state_length * self.data_dim, ), dtype=np.float32, name='observation')
self.data = self.preprocess_data(data.copy())
self.reset()
@property
def batched(self):
return False #True
@property
def batch_size(self):
return None #self._batch_size
@batch_size.setter
def batch_size(self, size):
self._batch_size = size
def preprocess_data(self, df):
def _log_rets(df):
log_returns = np.log(df / df.shift(1))
df = (log_returns - log_returns.mean()) / log_returns.std()
df = df.dropna()
return df
def min_max_scale_tensor(tensor):
min_val = tf.reduce_min(tensor)
max_val = tf.reduce_max(tensor)
return (tensor - min_val) / (max_val - min_val)
price_raw = df['Close'].copy()
for col in self.features:
tensor = tf.convert_to_tensor(df[col], dtype=tf.float32)
normalized_tensor = min_max_scale_tensor(tensor)
df[col] = normalized_tensor.numpy()
df = df.replace(0.0, np.nan)
df = df.interpolate(method='linear', limit=5, limit_area='inside')
df = df.ffill().bfill()
df[TARGET_FEATURE] = price_raw
df['Sharpe'] = 0
df['Position'] = 0
df['Action'] = ACT_HOLD
df['Holdings'] = 0.
df['Cash'] = float(self.balance)
df['Money'] = df['Holdings'] + df['Cash']
df['Returns'] = 0.
assert not df.isna().any().any()
return df
def action_spec(self):
"""Provides the specification of the action space."""
return self._action_spec
def observation_spec(self):
"""Provides the specification of the observation space."""
return self._observation_spec
def _reset(self):
"""Resets the environment state and prepares for a new episode."""
self.balance = self.initial_balance
self.current_step = self.state_length
self._episode_ended = False
self.total_shares = 0
self.data['Sharpe'] = 0
self.data['Position'] = 0
self.data['Action'] = ACT_HOLD
self.data['Holdings'] = 0.
self.data['Cash'] = float(self.balance)
self.data['Money'] = self.data.iloc[0]['Holdings'] + self.data.iloc[0]['Cash']
self.data['Returns'] = 0.
initial_observation = self._next_observation()
return ts.restart(initial_observation)
def _next_observation(self):
"""Generates the next observation based on the current step and history length."""
start_idx = max(0, self.current_step - self.state_length + 1)
end_idx = self.current_step + 1
obs = self.data[self.features].iloc[start_idx:end_idx]
# flatten because: https://stackoverflow.com/questions/67921084/dqn-agent-issue-with-custom-environment
obs_values = obs.values.flatten().astype(np.float32)
return obs_values
def _step(self, action):
"""Executes a trading action and updates the environment's state."""
if self._episode_ended:
return self.reset()
self.current_step += 1
current_price = self.data.iloc[self.current_step][TARGET_FEATURE]
assert not self.data.iloc[self.current_step].isna().any().any()
if action == ACT_LONG:
self._process_long_position(current_price)
elif action == ACT_SHORT:
prev_current_price = self.data.iloc[self.current_step - 1][TARGET_FEATURE]
self._process_short_position(current_price, prev_current_price)
elif action == ACT_HOLD:
self._process_hold_position()
elif action == ACT_NEUTRAL:
self._process_neutral_position(current_price)
else:
raise Exception(f"Invalid Actions: {action}")
self._update_financials()
done = self.current_step >= len(self.data) - 1
reward = self._calculate_reward_signal()
if done:
self._episode_ended = True
return ts.termination(self._next_observation(), reward)
else:
return ts.transition(self._next_observation(), reward, discount=self.reward_discount)
def _get_lower_bound(self, cash, total_shares, price):
"""
Compute the lower bound of the action space, particularly for short selling,
based on current cash, the number of shares, and the current price.
"""
delta = -cash - total_shares * price * (1 + self.epsilon) * (1 + self.transaction_cost)
if delta < 0:
lowerBound = delta / (price * (2 * self.transaction_cost + self.epsilon * (1 + self.transaction_cost)))
else:
lowerBound = delta / (price * self.epsilon * (1 + self.transaction_cost))
if np.isinf(lowerBound):
assert False
return lowerBound
def _process_hold_position(self):
step_idx = self.data.index[self.current_step]
self.data.at[step_idx, "Cash"] = self.data.iloc[self.current_step - 1]["Cash"]
self.data.at[step_idx, "Holdings"] = self.data.iloc[self.current_step - 1]["Holdings"]
self.data.at[step_idx, "Position"] = self.data.iloc[self.current_step - 1]["Position"]
self.data.at[step_idx, "Action"] = ACT_HOLD
def _process_neutral_position(self, current_price):
step_idx = self.data.index[self.current_step]
self.data.at[step_idx, "Cash"] = self.data.iloc[self.current_step - 1]['Cash'] - self.total_shares * current_price * (1 + self.transaction_cost)
self.data.at[step_idx, "Holdings"] = 0.0
self.data.at[step_idx, "Position"] = 0.0
self.data.at[step_idx, "Action"] = ACT_NEUTRAL
def _process_long_position(self, current_price):
step_idx = self.data.index[self.current_step]
self.data.at[step_idx, 'Position'] = 1
if self.data.iloc[self.current_step - 1]['Position'] == 1:
# more long
self.data.at[step_idx, 'Cash'] = self.data.iloc[self.current_step - 1]['Cash']
self.data.at[step_idx, 'Holdings'] = self.total_shares * current_price
elif self.data.iloc[self.current_step - 1]['Position'] == 0:
# new long
self.total_shares = math.floor(self.data.iloc[self.current_step - 1]['Cash'] / (current_price * (1 + self.transaction_cost)))
self.data.at[step_idx, 'Cash'] = self.data.iloc[self.current_step - 1]['Cash'] - self.total_shares * current_price * (1 + self.transaction_cost)
self.data.at[step_idx, 'Holdings'] = self.total_shares * current_price
self.data.at[step_idx, 'Action'] = 1
else:
# short to long
self.data.at[step_idx, 'Cash'] = self.data.iloc[self.current_step - 1]['Cash'] - self.total_shares * current_price * (1 + self.transaction_cost)
self.total_shares = math.floor(self.data.iloc[self.current_step]['Cash'] / (current_price * (1 + self.transaction_cost)))
self.data.at[step_idx, 'Cash'] = self.data.iloc[self.current_step]['Cash'] - self.total_shares * current_price * (1 + self.transaction_cost)
self.data.at[step_idx, 'Holdings'] = self.total_shares * current_price
self.data.at[step_idx, 'Action'] = 1
def _process_short_position(self, current_price, prev_price):
"""
Adjusts the logic for processing short positions to include lower bound calculations.
"""
step_idx = self.data.index[self.current_step]
self.data.at[step_idx, 'Position'] = -1
if self.data.iloc[self.current_step - 1]['Position'] == -1:
# Short more
low = self._get_lower_bound(self.data.iloc[self.current_step - 1]['Cash'], -self.total_shares, prev_price)
if low <= 0:
self.data.at[step_idx, 'Cash'] = self.data.iloc[self.current_step - 1]["Cash"]
self.data.at[step_idx, 'Holdings'] = -self.total_shares * current_price
else:
total_sharesToBuy = min(math.floor(low), self.total_shares)
self.total_shares -= total_sharesToBuy
self.data.at[step_idx, 'Cash'] = self.data.iloc[self.current_step - 1]["Cash"] - total_sharesToBuy * current_price * (1 + self.transaction_cost)
self.data.at[step_idx, 'Holdings'] = -self.total_shares * current_price
elif self.data.iloc[self.current_step - 1]['Position'] == 0:
# new short
self.total_shares = math.floor(self.data.iloc[self.current_step - 1]["Cash"] / (current_price * (1 + self.transaction_cost)))
self.data.at[step_idx, 'Cash'] = self.data.iloc[self.current_step - 1]["Cash"] + self.total_shares * current_price * (1 - self.transaction_cost)
self.data.at[step_idx, 'Holdings'] = -self.total_shares * current_price
self.data.at[step_idx, 'Action'] = -1
else:
# long to short
self.data.at[step_idx, 'Cash'] = self.data.iloc[self.current_step - 1]["Cash"] + self.total_shares * current_price * (1 - self.transaction_cost)
self.total_shares = math.floor(self.data.iloc[self.current_step]["Cash"] / (current_price * (1 + self.transaction_cost)))
self.data.at[step_idx, 'Cash'] = self.data.iloc[self.current_step]["Cash"] + self.total_shares * current_price * (1 - self.transaction_cost)
self.data.at[step_idx, 'Holdings'] = -self.total_shares * current_price
self.data.at[step_idx, 'Action'] = -1
def _update_financials(self):
"""Updates the financial metrics including cash, money, and returns."""
step_idx = self.data.index[self.current_step]
self.balance = self.data.iloc[self.current_step]['Cash']
self.data.at[step_idx,'Money'] = self.data.iloc[self.current_step]['Holdings'] + self.data.iloc[self.current_step]['Cash']
self.data.at[step_idx,'Returns'] = ((self.data.iloc[self.current_step]['Money'] - self.data.iloc[self.current_step - 1]['Money'])) / self.data.iloc[self.current_step - 1]['Money']
def _calculate_reward_signal(self, reward_clip=REWARD_CLIP):
"""
Calculates the reward for the current step. In the paper they use the %returns.
"""
return np.clip(self.data.iloc[self.current_step]['Returns'], -reward_clip, reward_clip)
def calculate_churn(self):
churn = 0
prev_position = 0
for i in range(1, self.current_step + 1):
current_position = self.data.at[self.data.index[i], 'Position']
action = self.data.at[self.data.index[i], 'Action']
if action in [ACT_LONG, ACT_SHORT] and current_position != prev_position:
churn += self.transaction_cost
prev_position = current_position
if self.current_step > 0:
churn /= self.current_step
return churn
def calculate_drawdown_metrics(self):
cumulative_returns = (1 + self.data['Returns'].iloc[:self.current_step + 1]).cumprod()
peak = cumulative_returns.expanding(min_periods=1).max()
drawdown = (cumulative_returns - peak) / peak
peak_dates = cumulative_returns[peak == cumulative_returns]
drawdown_durations = pd.Series(index=drawdown.index, dtype='timedelta64[ns]')
for date in drawdown.index:
recent_peak_date = peak_dates[peak_dates.index <= date].index[-1]
duration = date - recent_peak_date
drawdown_durations.at[date] = duration
drawdown_durations_days = drawdown_durations.dt.days
max_dd_duration_days = drawdown_durations_days.max()
return drawdown, max_dd_duration_days
def get_trade_stats(self, riskfree_rate=0.05):
rets = self.data['Returns'].iloc[:self.current_step + 1]
monthly_riskfree_rate = (1 + riskfree_rate)**(1/12) - 1
annualized_return = rets.mean() * 12
annualized_vol = rets.std() * np.sqrt(12)
sharpe_ratio = (rets.mean() - monthly_riskfree_rate) / rets.std() * np.sqrt(12)
downside_deviation = rets[rets < 0].std() * np.sqrt(12)
drawdowns, max_dd_duration_days = self.calculate_drawdown_metrics()
sortino_ratio = (rets.mean() - monthly_riskfree_rate) / downside_deviation
churn = self.calculate_churn()
return {
"Annualized Return": annualized_return,
"Annualized Vol": annualized_vol,
"Sharpe Ratio": sharpe_ratio,
"Downside Deviation": downside_deviation,
"Sortino Ratio": sortino_ratio,
"Max Drawdown": drawdowns.max(),
"Max Drawdown Days": max_dd_duration_days,
"Trade Churn": churn,
"Skewness": skew(rets.values),
"Kurtosis": kurtosis(rets.values)
}
def render(self, mode='human'):
print(f'Step: {self.current_step}, Balance: {self.balance}, Holdings: {self.total_shares}')
print(f"trade stats: {self.get_trade_stats()}")Test the environment:
stock= tickers[TARGET]
train_data = stock[stock.index < pd.to_datetime(SPLIT_DATE)].copy()
test_data = stock[stock.index >= pd.to_datetime(SPLIT_DATE)].copy()
train_env = TradingEnv(train_data)
utils.validate_py_environment(train_env, episodes=TRAIN_EPISODES)
test_env = TradingEnv(test_data)
utils.validate_py_environment(train_env, episodes=TRAIN_EPISODES//4)
print(f"TimeStep Specs: {train_env.time_step_spec()}")
print(f"Action Specs: {train_env.action_spec()}")
print(f"Reward Specs: {train_env.time_step_spec().reward}")
def execute_action_and_print_state(env, action):
next_time_step = env.step(np.array(action, dtype=np.int32))
print(f'Action taken: {action} at step: {env.current_step}')
# print(f'New state: {next_time_step.observation}')
print(f'New balance: {env.balance}')
print(f'Total shares: {env.total_shares}')
print(f'Reward: {next_time_step.reward}\n')
time_step = train_env.reset()
# print(f'Initial state: {time_step.observation}')
# Some dryruns to validate our env logic: Buy, Sell, we should have a positive balance with TSLA
execute_action_and_print_state(train_env, ACT_HOLD)
execute_action_and_print_state(train_env, ACT_LONG)
execute_action_and_print_state(train_env, ACT_SHORT)
execute_action_and_print_state(train_env, ACT_HOLD)
execute_action_and_print_state(train_env, ACT_LONG)
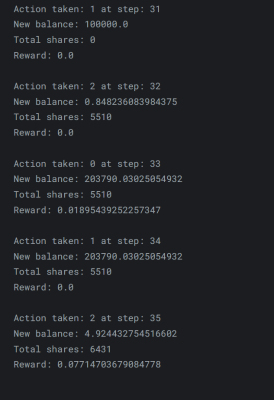
九、深度 Q-Network 架构
深度 Q 神经网络架构 (DQN) 近似于动作值函数 π∗(at|st) 的 Q 表。这是一个近似值,因为您可以使用 Q-Table 的组合数量是巨大的且无法处理的。
Q 网络也称为策略模型。我们还将在我们的架构中利用目标 Q 网络。Tha 目标模型的更新比 Q-Network 少,并且有助于稳定训练过程,因为 Q-Network 被训练以减少其输出和目标网络(更稳定的值)。
最后,我们将添加一个回放记忆来为我们的模型提供样本数据。内存是固定大小的循环内存(因此它会“忘记”旧内存),并且在每个固定频率下,模型使用内存来计算其预测的 Q 值与内存中执行的 Q 值之间的损失。
十、强化学习流程
一张图片胜过千言万语;下面的流程图将指导我们进行整个训练和更新目标模型:
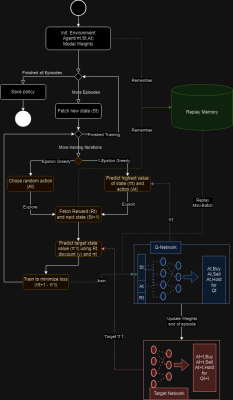
首先,我们启动了环境 St 和动作状态 Qt。
然后,我们运行多次迭代来训练模型并记住状态、动作和预测的 Q 值。在每次迭代中,将发生以下事件:
- 获取状态。
- 采取随机行动(ε贪婪)或预测给定当前状态下的行动的 Q 值,前者称为探索,后者称为利用。ε会随着时间的流逝而衰减,随着模型的学习,它应该探索得更少。
- 在预测 Q 值时,它将使用策略模型。无论是探索还是爆炸,它都会保存状态、动作和给定 Q 值的记忆。
- 通过从目标网络获取最大预测来计算目标 Q 值。从前面的公式 rt + γt * Qtarget(s_t+1, a_t+1) 中,gamma γ 是贴现因子。
- 重新调整策略模型,以最小化不同模型的 Q 值差异(损失)。训练使用来自回放记忆的采样状态。
- 在剧集结束时,或者我们选择的任何时间间隔,我们将策略模型的余量复制到目标模型。
def create_q_network(env, fc_layer_params=LAYERS, dropout_rate=DROPOUT, l2_reg=L2FACTOR):
"""
Creates a Q-Network with dropout and batch normalization.
Parameters:
- env: The environment instance.
- fc_layer_params: Tuple of integers representing the number of units in each dense layer.
- dropout_rate: Dropout rate for dropout layers.
- l2_reg: L2 regularization factor.Returns:
- q_net: The Q-Network model.
"""
env = tf_py_environment.TFPyEnvironment(env)
action_tensor_spec = tensor_spec.from_spec(env.action_spec())
num_actions = action_tensor_spec.maximum - action_tensor_spec.minimum + 1
layers = []
for num_units in fc_layer_params:
layers.append(tf.keras.layers.Dense(
num_units,
activation=None,
kernel_initializer=tf.keras.initializers.VarianceScaling(scale=2.0, mode='fan_in', distribution='truncated_normal'),
kernel_regularizer=tf.keras.regularizers.l2(l2_reg)))
layers.append(tf.keras.layers.BatchNormalization())
layers.append(tf.keras.layers.LeakyReLU())
layers.append(tf.keras.layers.Dropout(dropout_rate))
q_values_layer = tf.keras.layers.Dense(
num_actions,
activation=None,
kernel_initializer=tf.keras.initializers.GlorotNormal(),
bias_initializer=tf.keras.initializers.GlorotNormal(),
kernel_regularizer=tf.keras.regularizers.l2(l2_reg))
q_net = sequential.Sequential(layers + [q_values_layer])
return q_net
def create_agent(q_net, env, t_q_net = None, optimizer = None, eps=EPSILON_START, learning_rate=LEARN_RATE, gradient_clipping = GRAD_CLIP):
"""
Creates a DQN agent for a given environment with specified configurations.
Parameters:
- q_net (tf_agents.networks.Network): The primary Q-network for the agent.
- env (tf_agents.environments.PyEnvironment or tf_agents.environments.TFPyEnvironment):
The environment the agent will interact with. A TFPyEnvironment wrapper is applied
if not already wrapped.
- t_q_net (tf_agents.networks.Network, optional): The target Q-network for the agent.
If None, no target network is used.
- optimizer (tf.keras.optimizers.Optimizer, optional): The optimizer to use for training the agent.
If None, an Adam optimizer with exponential decay learning rate is used.
- eps (float): The epsilon value for epsilon-greedy exploration.
- learning_rate (float): The initial learning rate for the exponential decay learning rate schedule.
Ignored if an optimizer is provided.
- gradient_clipping (float): The value for gradient clipping. If 1., no clipping is applied.
Returns:
- agent (tf_agents.agents.DqnAgent): The initialized and configured DQN agent.
"""
if optimizer is None:
lr_schedule = tf.keras.optimizers.schedules.ExponentialDecay(learning_rate, decay_steps=1000, decay_rate=0.96, staircase=True)
optimizer = tf.keras.optimizers.Adam(learning_rate=lr_schedule)
env = tf_py_environment.TFPyEnvironment(env)
# see: https://www.tensorflow.org/agents/api_docs/python/tf_agents/agents/DqnAgent
agent = dqn_agent.DqnAgent(
env.time_step_spec(),
env.action_spec(),
q_network=q_net,
target_q_network = t_q_net,
target_update_period = TARGET_UPDATE,
optimizer=optimizer,
epsilon_greedy = eps,
reward_scale_factor = 1,
gradient_clipping = gradient_clipping,
td_errors_loss_fn=common.element_wise_huber_loss,
train_step_counter=tf.compat.v1.train.get_or_create_global_step(),
name="TradeAgent")
agent.initialize()
print(agent.policy)
print(agent.collect_policy)
return agent
with strategy.scope():
q_net = create_q_network(train_env)
t_q_net = create_q_network(train_env)
agent = create_agent(q_net, train_env, t_q_net=t_q_net)十一、交易操作
使用 TensorFlow 代理的框架,培训我们的巴甫洛夫交易员应该比自己构建架构更容易。
交易模拟器类将准备所有必需的变量。在这种情况下,它将使用 DeepMind 的 Reverb 初始化回放内存,并为代理创建收集器策略。与用于预测目标 Q 值的评估策略 (π(at|ht)) 不同,收集器将探索和收集带有动作的数据及其对内存的结果值,记忆被保存为轨迹 (τ) 在 tensorflow 中,它是当前观察到的状态 (ot)、采取的行动 (at)、收到的奖励 (r_t+1) 和以下观察到的状态 (o_t+1) 的集合,形式化为 r=(o_t-1, a_t-1, rt, ot, dt),其中 dt 是结束状态的标志,如果这是最后一次观测值。
为了给我们的智能体提供学习的机会,我们将使用一个高 epsilon 让它进行大量探索,并使用以下公式慢慢衰减它:

哪里:
- ε_decayed 是当前步骤的衰减 epsilon 值,
- ε_initial 是训练开始时的初始 epsilon 值,我们将其设置为 1,这意味着它仅在开始时进行探索。
- 我们希望代理利用的最终值是环境,ε_final最好是在部署时。
- step 是训练过程中的当前步骤或迭代,decay_steps 是控制速率的参数,在本例中为 1000。随着台阶接近尾声,衰变会越来越小。
让我们编写模拟器代码来训练和评估我们的代理,在 TPU 上它运行 2 小时,在 CPU 上它可以运行长达 8 小时:
import tensorflow as tf
class CustomMetrics(tf.Module):
def __init__(self, name=None):
super(CustomMetrics, self).__init__(name=name)
self.total_returns = tf.Variable([], dtype=tf.float32, trainable=False, shape=tf.TensorShape(None))
self.average_returns = tf.Variable([], dtype=tf.float32, trainable=False, shape=tf.TensorShape(None))
self.sharpe_ratios = tf.Variable([], dtype=tf.float32, trainable=False, shape=tf.TensorShape(None))
self.losses = tf.Variable([], dtype=tf.float32, trainable=False, shape=tf.TensorShape(None))
def update_metrics(self, losses=None, total_return=None, average_return=None, sharpe_ratio=None):
if total_return is not None:
self.total_returns.assign(tf.concat([self.total_returns.value(), [total_return]], axis=0))
if total_return is not None:
self.average_returns.assign(tf.concat([self.average_returns.value(), [average_return]], axis=0))
if total_return is not None:
self.sharpe_ratios.assign(tf.concat([self.sharpe_ratios.value(), [sharpe_ratio]], axis=0))
if losses is not None:
self.losses.assign(tf.concat([self.losses.value(), [losses]], axis=0))
class TradingSimulator:
def __init__(self, env, eval_env, agent, episodes=TRAIN_EPISODES,
batch_size=BATCH_SIZE, num_eval_episodes=TEST_INTERVALS,
collect_steps_per_iteration=INIT_COLLECT,
replay_buffer_max_length=MEMORY_LENGTH ,
num_iterations = TOTAL_ITERS, log_interval=LOG_INTERVALS,
eval_interval=None, global_step=None):
self.py_env = env
self.env = tf_py_environment.TFPyEnvironment(self.py_env)
self.py_eval_env = eval_env
self.eval_env = tf_py_environment.TFPyEnvironment(self.py_eval_env)
self.agent = agent
self.episodes = episodes
self.log_interval = log_interval
self.eval_interval = eval_interval
self.global_step = global_step
self.batch_size = batch_size
self.num_eval_episodes = num_eval_episodes
self.collect_steps_per_iteration = collect_steps_per_iteration
self.replay_buffer_max_length = replay_buffer_max_length
self.num_iterations = num_iterations
self.policy = self.agent.policy
self.collect_policy = self.agent.collect_policy
self.random_policy = random_tf_policy.RandomTFPolicy(
self.env.time_step_spec(),
self.env.action_spec())
self.replay_buffer_signature = tensor_spec.from_spec(
self.agent.collect_data_spec)
self.replay_buffer_signature = tensor_spec.add_outer_dim(
self.replay_buffer_signature)
def init_memory(self, table_name = 'uniform_table'):
self.table = reverb.Table(
table_name,
max_size=self.replay_buffer_max_length,
sampler=reverb.selectors.Uniform(),
remover=reverb.selectors.Fifo(),
rate_limiter=reverb.rate_limiters.MinSize(1),
signature=self.replay_buffer_signature)
self.reverb_server = reverb.Server([self.table])
self.replay_buffer = reverb_replay_buffer.ReverbReplayBuffer(
self.agent.collect_data_spec,
table_name=table_name,
sequence_length=2,
local_server=self.reverb_server)
self.rb_observer = reverb_utils.ReverbAddTrajectoryObserver(self.replay_buffer.py_client, table_name, sequence_length=2)
self.dataset = self.replay_buffer.as_dataset(num_parallel_calls=3, sample_batch_size=self.batch_size, num_steps=2).prefetch(3)
return self.dataset, iter(self.dataset)
def eval_metrics(self, num_eval_episodes):
@tf.function
def _eval_step():
time_step = self.eval_env.reset()
episode_returns = tf.TensorArray(dtype=tf.float32, size=0, dynamic_size=True, clear_after_read=False)
while not time_step.is_last():
action_step = self.policy.action(time_step)
time_step = self.eval_env.step(action_step.action)
rewards = time_step.reward
episode_returns = episode_returns.write(episode_returns.size(), rewards)
episode_returns_stacked = episode_returns.stack()
cumulative_returns = tf.math.cumprod(episode_returns_stacked + 1) - 1
total_episode_return = cumulative_returns[-1]
episode_avg_return = tf.reduce_mean(episode_returns_stacked)
episode_std_dev = tf.math.reduce_std(episode_returns_stacked)
episode_sharpe_ratio = tf.cond(
episode_std_dev > 0,
lambda: episode_avg_return / episode_std_dev,
lambda: tf.constant(0.0)
)
return total_episode_return, episode_avg_return, episode_std_dev, episode_sharpe_ratio
# Initialize lists to hold the metrics for all episodes
total_returns_list = []
episode_avg_returns_list = []
episode_std_devs_list = []
episode_sharpe_ratios_list = []
for i in tqdm(range(0, num_eval_episodes), desc=f"Eval for {num_eval_episodes}"):
total_episode_return, episode_avg_return, episode_std_dev, episode_sharpe_ratio = _eval_step()
total_returns_list.append(total_episode_return)
episode_avg_returns_list.append(episode_avg_return)
episode_std_devs_list.append(episode_std_dev)
episode_sharpe_ratios_list.append(episode_sharpe_ratio)
# Convert lists to tensors for returning
total_returns = tf.convert_to_tensor(total_returns_list)
episode_avg_returns = tf.convert_to_tensor(episode_avg_returns_list)
episode_std_devs = tf.convert_to_tensor(episode_std_devs_list)
episode_sharpe_ratios = tf.convert_to_tensor(episode_sharpe_ratios_list)
return total_returns, episode_avg_returns, episode_std_devs, episode_sharpe_ratios
def train(self, checkpoint_path=MODELS_PATH, initial_epsilon= EPSILON_START, final_epsilon = EPSILON_END, decay_steps=EPSILON_DECAY):
@tf.function
def _train_step(experience, agent, metrics, global_step, initial_epsilon, final_epsilon, decay_steps):
train_loss = agent.train(experience).loss
metrics.update_metrics(losses=train_loss)
decayed_epsilon = final_epsilon + (initial_epsilon - final_epsilon) * tf.math.exp(-1. * tf.cast(global_step, tf.float32) / decay_steps)
agent.collect_policy._epsilon = decayed_epsilon
return train_loss
print("Preparing replay memory and dataset")
_, iterator = self.init_memory()
self.metrics = CustomMetrics()
self.global_step = tf.compat.v1.train.get_or_create_global_step()
checkpoint_dir = os.path.join(checkpoint_path, 'checkpoint')
train_checkpointer = common.Checkpointer(
ckpt_dir=checkpoint_dir,
max_to_keep=1,
agent=agent,
metrics=self.metrics,
policy=agent.policy,
replay_buffer=self.replay_buffer,
global_step=self.global_step
)
status = train_checkpointer.initialize_or_restore()
self.global_step = tf.compat.v1.train.get_global_step()
print(f'Next step restored: {self.global_step.numpy()} status: {status}')
self.policy = agent.policy
self.agent.train = common.function(self.agent.train)
self.agent.train_step_counter.assign(self.global_step )
time_step = self.py_env.reset()
collect_driver = py_driver.PyDriver(
self.py_env,
py_tf_eager_policy.PyTFEagerPolicy(self.agent.collect_policy, use_tf_function=True),
[self.rb_observer],
max_steps=self.collect_steps_per_iteration)
print(f"Running training starting {self.global_step.numpy()} to {self.num_iterations}")
for _ in tqdm(range(self.global_step.numpy(), self.num_iterations), desc=f"Training for {self.global_step.numpy() - self.num_iterations}"):
time_step, _ = collect_driver.run(time_step)
experience, _ = next(iterator)
train_loss = _train_step(experience, agent, self.metrics, self.global_step, initial_epsilon= initial_epsilon, final_epsilon = final_epsilon, decay_steps=decay_steps)
if self.global_step.numpy() % self.log_interval == 0:
print(f'step = {self.global_step.numpy()}: loss = {train_loss}')
# Later call: saved_policy = tf.saved_model.load(policy_dir)
train_checkpointer.save(self.global_step)
if (self.eval_interval is not None) and (self.global_step.numpy() % self.eval_interval == 0):
total_returns, episode_avg_returns, episode_std_devs, episode_sharpe_ratios= self.eval_metrics(self.eval_interval // 2)
tr = np.mean(total_returns)
av = np.mean(episode_avg_returns)
sr = np.mean(episode_sharpe_ratios)
sd = np.mean(episode_std_devs)
print(f'step = {self.global_step.numpy()}: Average Return = {av}, Total Return = {tr}, Avg Sharpe = {sr} -- Saving {self.global_step} Checkpoint')
self.metrics.update_metrics(total_return=tr, average_return=av, sharpe_ratio=sr)
train_checkpointer.save(self.global_step)
print(f'\nTraining completed. Loss: {np.mean(self.metrics.losses.numpy()):.4f}')
policy_dir = os.path.join(checkpoint_path, 'policy')
tf_policy_saver = policy_saver.PolicySaver(agent.policy)
tf_policy_saver.save(policy_dir)
self.zip_directories(checkpoint_path)
print("Policy saved")
self.rb_observer.close()
self.reverb_server.stop()
return self.metrics
def load_and_eval_policy(self, policy_path=MODELS_PATH, eval_interval=TEST_INTERVALS//4):
policy_dir = os.path.join(policy_path, 'policy')
self.policy = tf.saved_model.load(policy_dir)
total_returns, avg_return, _, sharpe_ratio = self.eval_metrics(eval_interval)
print(f'Average Return = {np.mean(avg_return)}, Total Return = {np.mean(total_returns)}, Sharpe = {np.mean(sharpe_ratio)}')
return self.policy, total_returns, avg_return, sharpe_ratio
def clear_directories(self, directories = MODELS_PATH):
try:
if IN_COLAB:
shutil.rmtree(f"{GDRIVE}/MyDrive/{directories}")
print(f"Successfully cleared {GDRIVE}/MyDrive/{directories}")
shutil.rmtree(directories)
print(f"Successfully cleared {directories}")
except Exception as e:
print(f"Error clearing {directories}: {e}")
def zip_directories(self, directories = MODELS_PATH, output_filename=f'{MODELS_PATH}/model_files'):
"""
Creates a zip archive containing the specified directories.
Parameters:
- directories: List of paths to directories to include in the archive.
- output_filename: The base name of the file to create, including the path,
minus any format-specific extension. Default is 'training_backup'.
"""
if IN_COLAB:
archive_path = shutil.make_archive(f'{GDRIVE}/MyDrive/{directories}', 'zip', root_dir='.', base_dir=directories)
print(f"Archived {GDRIVE}/MyDrive/{directories}")
else:
archive_path = shutil.make_archive(output_filename, 'zip', root_dir='.', base_dir=directories)
print(f"Archived {directories} into {archive_path}")
def plot_performance(self, metrics):
"""
Plot the training performance including average returns and Sharpe Ratios on the same plot,
with returns on the left y-axis and Sharpe Ratios on the right y-axis.
"""
fig, axs = plt.subplots(1, 2, figsize=(18, 4))
axs[0].set_xlabel('Iterations')
axs[0].set_ylabel('Average Return')
axs[0].plot(range(0, len(metrics.average_returns.numpy())), metrics.average_returns.numpy(), label='Average Return', color="blue")
axs[0].tick_params(axis='y')
axs[0].legend(loc="upper right")
ax12 = axs[0].twinx()
ax12.set_ylabel('Sharpe Ratio')
ax12.plot(range(0, len(metrics.sharpe_ratios.numpy())), metrics.sharpe_ratios.numpy(), label='Sharpe Ratio', color="yellow")
ax12.tick_params(axis='y')
ax12.legend(loc="upper left")
axs[1].set_xlabel('Iterations')
axs[1].set_ylabel('Loss')
axs[1].plot(range(0, len(metrics.losses.numpy())), metrics.losses.numpy(), label='Loss', color="red")
axs[1].tick_params(axis='y')
axs[1].legend()
fig.tight_layout()
plt.title('Training Performance: Average Returns and Sharpe Ratios')
plt.show()
def plot_returns_and_actions(self):
"""
Steps through the environment's data using the given policy and plots the actions,
along with a subplot for cumulative returns.
"""
data = self.py_eval_env.data.copy()
actions = [ACT_HOLD]
cumulative_returns = [0]
time_step = self.eval_env.reset()
for _ in tqdm(range(1, len(data)), desc=f"Live actions for {len(data)} iters"):
action_step = self.policy.action(time_step)
time_step = self.eval_env.step(action_step.action)
actions.append(action_step.action)
if len(cumulative_returns) > 1:
cumulative_returns.append(cumulative_returns[-1] + time_step.reward.numpy()[-1] )
else:
cumulative_returns.append(time_step.reward.numpy()[-1])
data['Action'] = actions
data['Cumulative_Returns'] = np.cumsum(cumulative_returns)
fig, axs = plt.subplots(2, 1, figsize=(18, 8), gridspec_kw={'height_ratios': (3, 1)})
axs[0].plot(data.index, data[TARGET_FEATURE], label='Close', color='k', alpha=0.6)
buys = data[data['Action'] == ACT_LONG]
axs[0].scatter(buys.index, buys[TARGET_FEATURE], label='Buy', color='green', marker='^', alpha=1)
sells = data[data['Action'] == ACT_SHORT]
axs[0].scatter(sells.index, sells[TARGET_FEATURE], label='Sell', color='red', marker='v', alpha=1)
axs[0].set_ylabel('Close ($)')
axs[0].set_title('Trading Actions and Close Prices')
axs[0].legend()
axs[1].plot(data.index, data['Cumulative_Returns'], label='Cumulative Returns', color='blue')
axs[1].set_ylabel('Cumulative Returns')
axs[1].set_title('Cumulative Returns')
axs[1].legend()
for ax in axs:
ax.xaxis.set_major_locator(mdates.AutoDateLocator())
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m-%d'))
fig.autofmt_xdate()
plt.xlabel('Date')
plt.show()
with strategy.scope():
sim = TradingSimulator(train_env, test_env, agent=agent)
try:
%%time
except:
pass
# Uncomment if you are training a new policy
def train():
with strategy.scope():
loss = sim.train()
sim.plot_performance(loss)
sim.eval_metrics(25)
train()在训练过程中,我们可以观察到 epsilon 贪婪策略的影响,其中初始训练事件会产生很高的损失,因为代理会采取随机操作:
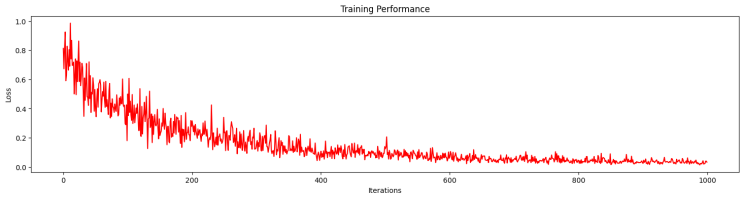
培训完成后,我们评估新策略并可视化其结果:

鉴于我们目前设置的 0.6 epsilon 折扣和 +25% 的负回报的小惩罚,该代理的表现相当不错。
{'Annualized Return': 0.4157554099733984,
'Annualized Vol': 0.526509836743958,
'Sharpe Ratio': 0.6969680274041493,
'Downside Deviation': 0.3457139483184213,
'Sortino Ratio': 0.00421213131836031,
'Max Drawdown': 0.0,
'Max Drawdown Days': 261,
'Trade Churn': 0.0,
'Skewness': 0.7191282724766412,
'Kurtosis': 5.44751948119778}比较了本文的基准测试及其 TQDM 架构,我们在 Tensorflow 设置和架构方面做得更好(我们对一些超参数进行了猜测),除了回撤持续时间、Sharpe 和 Sortino 比率:
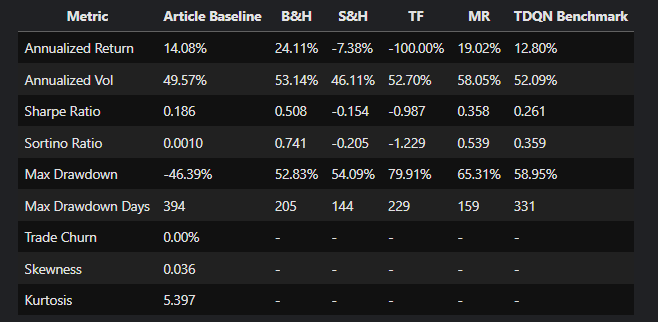
让我们尝试获取更多的短期收益,我们将 epsilon 降低到 0.3,将我们的代理变成“日内交易者”:
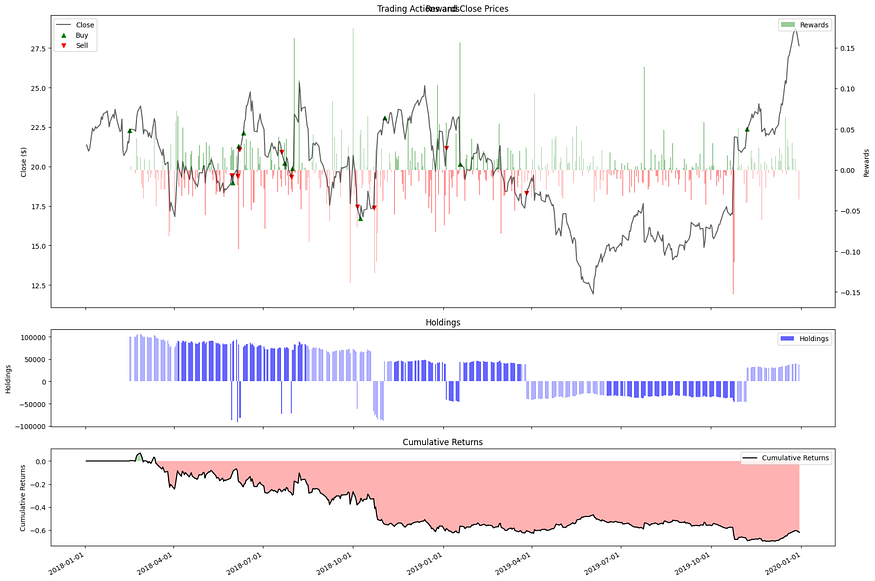
{'Annualized Return': -0.350555829680856,
'Annualized Vol': 0.5188582006668314,
'Sharpe Ratio': -0.7696721701935054,
'Downside Deviation': 0.37696770151282327,
'Sortino Ratio': -0.00420387492724144,
'Max Drawdown': 0.0,
'Max Drawdown Days': 672,
'Trade Churn': 0.0,
'Skewness': 0.352979579434461,
'Kurtosis': 6.181142153328116}追逐短期收益并不顺利,代理处于永久回撤状态!
十二、三组实验
接下来,我们将通过在以下 3 个实验中增强数据和奖励函数来进行测试。
12.1 实验 1 — 夏普比率作为奖励
这将是我们的下一个奖励功能,假设我们的代理人可以将其投资组合的波动性降至最低。在我们的例子中,我们需要将过去交易时段的数量(最多 252 个,一年中的交易日)平方,以给出年化夏普作为奖励:
def _calculate_sharpe_reward_signal(self, risk_free_rate=0.05, periods_per_year=252, reward_clip=REWARD_CLIP):
"""
Calculates the annualized Sharpe ratio up to the CURRENT STEP.Parameters:
- risk_free_rate (float): The annual risk-free rate. It will be adjusted to match the period of the returns.
- periods_per_year (int): Number of periods in a year (e.g., 252 for daily, 12 for monthly).
Returns:
- float: The annualized Sharpe ratio as reward.
"""
period_risk_free_rate = (1 + risk_free_rate) ** (1 / periods_per_year) - 1
observed_returns = self.data['Returns'].iloc[:self.current_step + 1]
excess_returns = observed_returns - period_risk_free_rate
mean_excess_return = np.mean(excess_returns)
std_dev_returns = np.std(observed_returns)
sharpe_ratio = mean_excess_return / std_dev_returns if std_dev_returns > 0 else 0
annual_sr = sharpe_ratio * np.sqrt(periods_per_year)
self.data.at[self.data.index[self.current_step], 'Sharpe'] = annual_sr
return np.clip(annual_sr, -reward_clip, reward_clip)结果是有希望的,比基线要好——但看看这个回撤的持续时间!
{'Annualized Return': 0.2483099753903375,
'Annualized Vol': 0.5315927401982844,
'Sharpe Ratio': 0.3753156743014152,
'Downside Deviation': 0.3649215721069904,
'Sortino Ratio': 0.0021695799842264578,
'Max Drawdown': -0.5284848329394528,
'Max Drawdown Days': 493,
'Trade Churn': 0.0,
'Skewness': 0.547255666186771,
'Kurtosis': 5.424081523143858}从图表上看,我们看到它只交易了一次!我们应该改变折扣,以防止它变成只买入并持有的政策。
12.2 实验 2:技术分析 (TA) 信号
使用 Pandas-TA 库,我们用以下信号来增强我们的时间序列:
- 移动平均收敛散度 (MACD) 可用于确认趋势的存在。此外,它还可以发现与价格的背离,这可能预示着潜在的反转。MACD 由 12 天快速移动平均线 (MA)、26 天慢移动平均线 (MA) 和信号创建,信号是它们差值的 9 天指数移动平均线 (EMA)。
- 平均真实范围 (ATR) 将表明代理价格波动及其幅度,这将暗示环境的波动性。它是通过分解价格极端值的 14 天移动平均线构建的。
下面的代码创建以下信号:
stock_df = tickers[TARGET].copy()
macd = MACD(close=stock_df["Close"], window_slow=26, window_fast=12, window_sign=9, fillna=True)
stock_df['MACD'] = macd.macd()
stock_df['MACD_HIST'] = macd.macd_diff()
stock_df['MACD_SIG'] = macd.macd_signal()
atr = AverageTrueRange(stock_df["High"], stock_df["Low"], stock_df["Close"], window = 14, fillna = True)
stock_df['ATR'] = atr.average_true_range()
ema = EMAIndicator(stock_df["Close"], window = 14, fillna = True)
stock_df['EMA'] = ema.ema_indicator()
stock_df与基线和夏普变体相比,结果很差,这是一个失败者,整个事件都是回撤:
{'Annualized Return': 0.08037565358057806,
'Annualized Vol': 0.5327752235074609,
'Sharpe Ratio': 0.05927596580709699,
'Downside Deviation': 0.36637039877343286,
'Sortino Ratio': 0.00034205956635066734,
'Max Drawdown': 0.0,
'Max Drawdown Days': 672,
'Trade Churn': 0.0,
'Skewness': 0.5699760228074306,
'Kurtosis': 5.441197183719924}视觉结果如下所示:
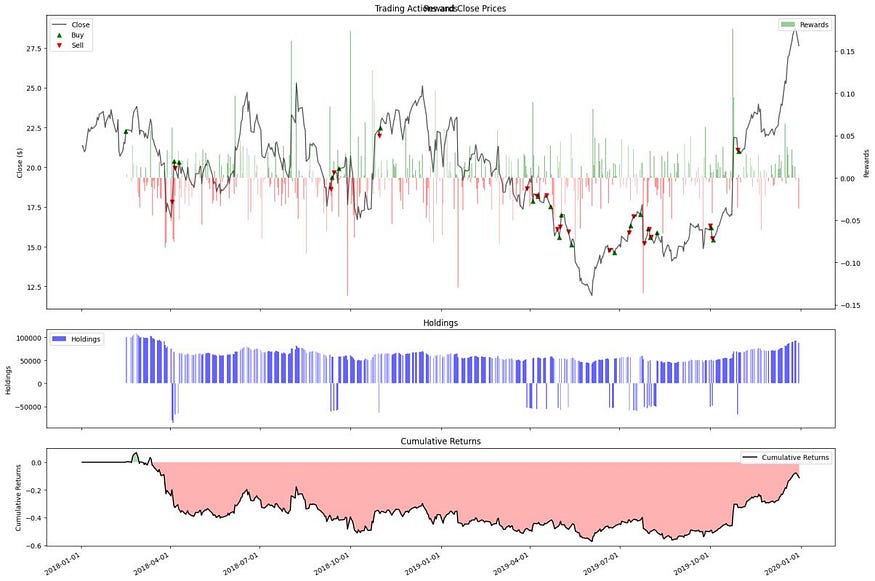
TA 信号导致代理在错误的时间搅动。从图中我们可以观察到,从战术上讲,代理在交易后立即看到了可观的奖励(奖励条),但是当它的奖励进入负值区域时,代理做了所有错误的行为。
请注意,这两个信号都是滞后信号,这可以解释为什么代理行动太晚。
如果我们有时间,我们会尝试使用单个 TA 和/或折扣因素,以给予代理更多的战略激励。
12.3 实验3:宏信号
在此实验中,我们将通过以下时间序列为智能体提供对其宏观环境的见解:
- VIX — 当前时期的波动率和恐惧指数。
- 10年期国库券收益率——作为通胀的指标。
- 标准普尔 500 指数 — 市场风险因素。
对于代码,它只是添加以下时间序列:
RATES_INDEX = "^TNX" # 10 Year Treasury Note Yield
VOLATILITY_INDEX = "^VIX" # CBOE Volatility Index
SMALLCAP_INDEX = "^RUT" # Russell 2000 Index
GOLD_INDEX = "GC=F" # Gold futures
TICKER_SYMBOLS = [TARGET, RATES_INDEX, VOLATILITY_INDEX, SMALLCAP_INDEX, GOLD_INDEX]
stock_df[VOLATILITY_INDEX] = tickers[VOLATILITY_INDEX]["Close"]
stock_df[RATES_INDEX] = tickers[RATES_INDEX]["Close"]
stock_df[SMALLCAP_INDEX] = tickers[SMALLCAP_INDEX]["Close"]
stock_df[GOLD_INDEX] = tickers[GOLD_INDEX]["Close"]
stock_df[MARKET] = tickers[MARKET]["Close"]
stock_df为我们提供了出色的结果,一个可以访问影响其边界环境的信息的代理可以创建优于我们的基线和所有论文基准的策略:
{'Annualized Return': 0.7375854975646395,
'Annualized Vol': 0.48576500545216406,
'Sharpe Ratio': 1.417950247927827,
'Downside Deviation': 0.30906051769218884,
'Sortino Ratio': 0.008843886276718567,
'Max Drawdown': -0.38977234510237335,
'Max Drawdown Days': 142,
'Trade Churn': 0.0,
'Skewness': 0.7135103541646352,
'Kurtosis': 4.722124713372126}让我们想象一下代理的行为,它所做的最后一个严重错误,代理的行为就像一个明智的人类交易员:
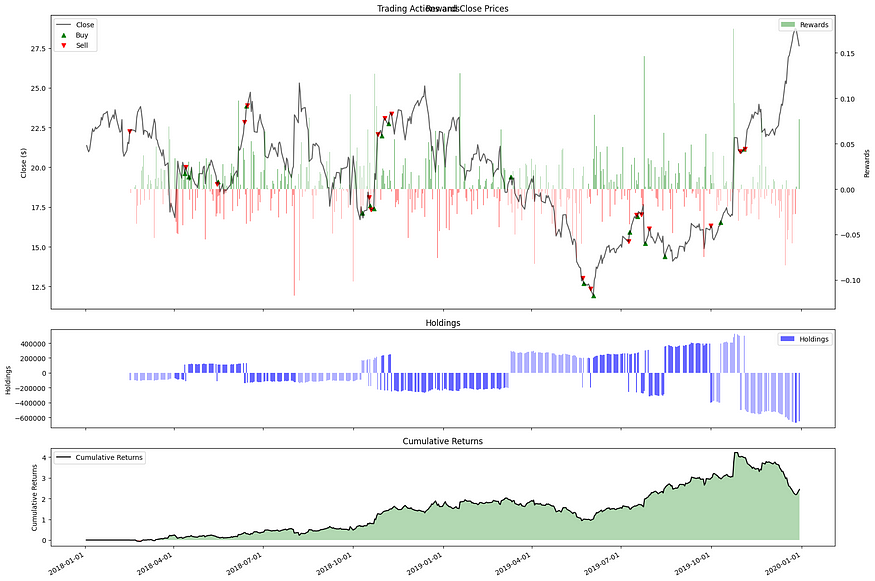
十三、结论
在本文中,我们使用我们的信号和改进的 Tensorflow 代理框架和架构,调整并改进了 Théate、Thibaut 和 Ernst, Damien (2021) 的 Trading Deep Q-Network (TDQN) 算法。
我们的代理现在可以确定最佳交易头寸(买入、卖出或持有),以在模拟环境中最大化其投资组合回报。通过数据增强,代理的性能可以大幅改变,如下表所示:
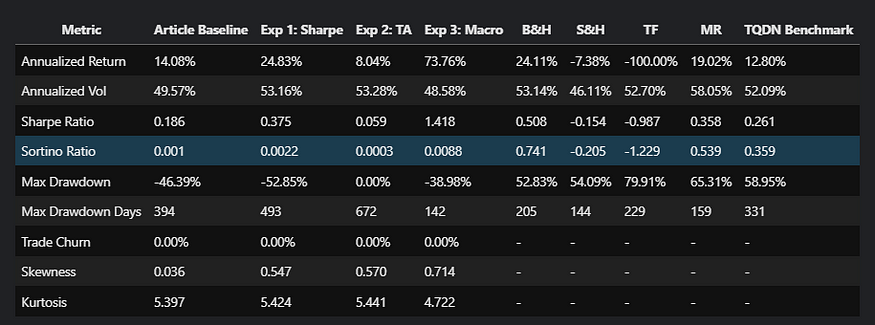
这位巴甫洛夫交易员是一个有趣的研究和测试练习。尽管测试和实现的回报和环境是不现实的,并且设置在现实世界环境中会失败。
参考文章: