今日任务
- 二叉树的理论基础 ( 参考: 代码随想录)
二叉树种类
二叉树是一种基础数据结构,在算法面试中都是常客,也是众多数据结构的基石。二叉树的定义 和链表是差不多的,相对于链表 ,二叉树的节点里多了一个指针, 有两个指针,指向左右孩子。
//Go: 二叉树的定义
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
//Python: 二叉树的定义
class TreeNode:
def __init__(self, val, left = None, right = None):
self.val = val
self.left = left
self.right = right解题过程中二叉树有两种主要的形式:满二叉树、完全二叉树。
满二叉树
如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。深度为 k, 节点个数为( 2^k - 1),例如下图的满二叉树 深度为 4、节点数为 2^4-1=15 个节点
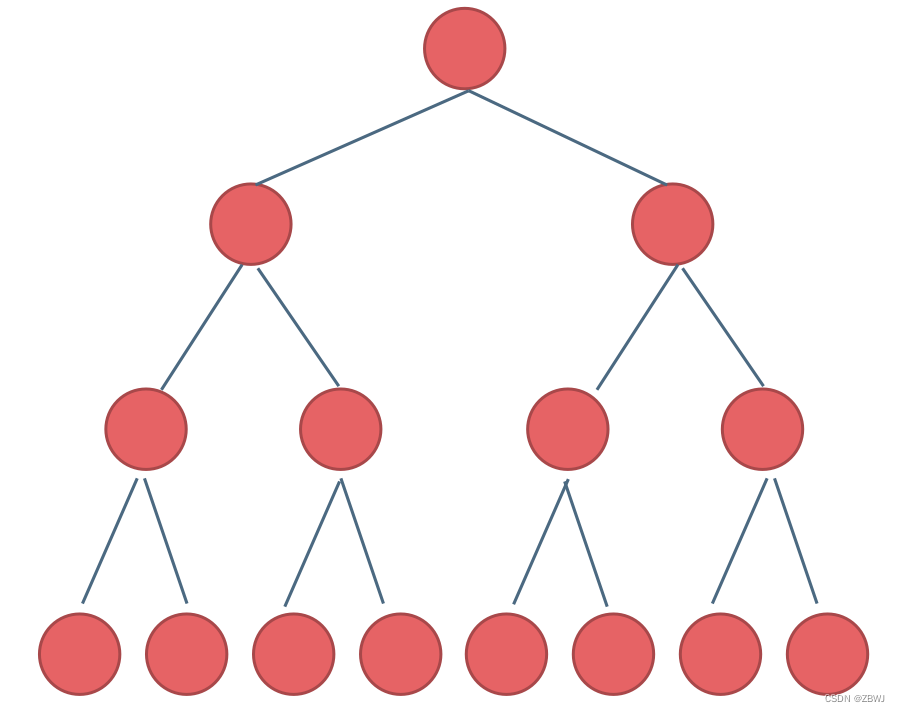
完全二叉树
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置(这句话可能会不理解, 实际就是 “完全二叉树的底部一定是从左到右连续的” )。若最底层为第 h 层(h从1开始),则该层包含 1~ 2^(h-1) 个节点 , 例如下面一个 4 层的完全二叉树, 第 4 层的节点个数就是 1~2^(4-1) 即 1~8 个.
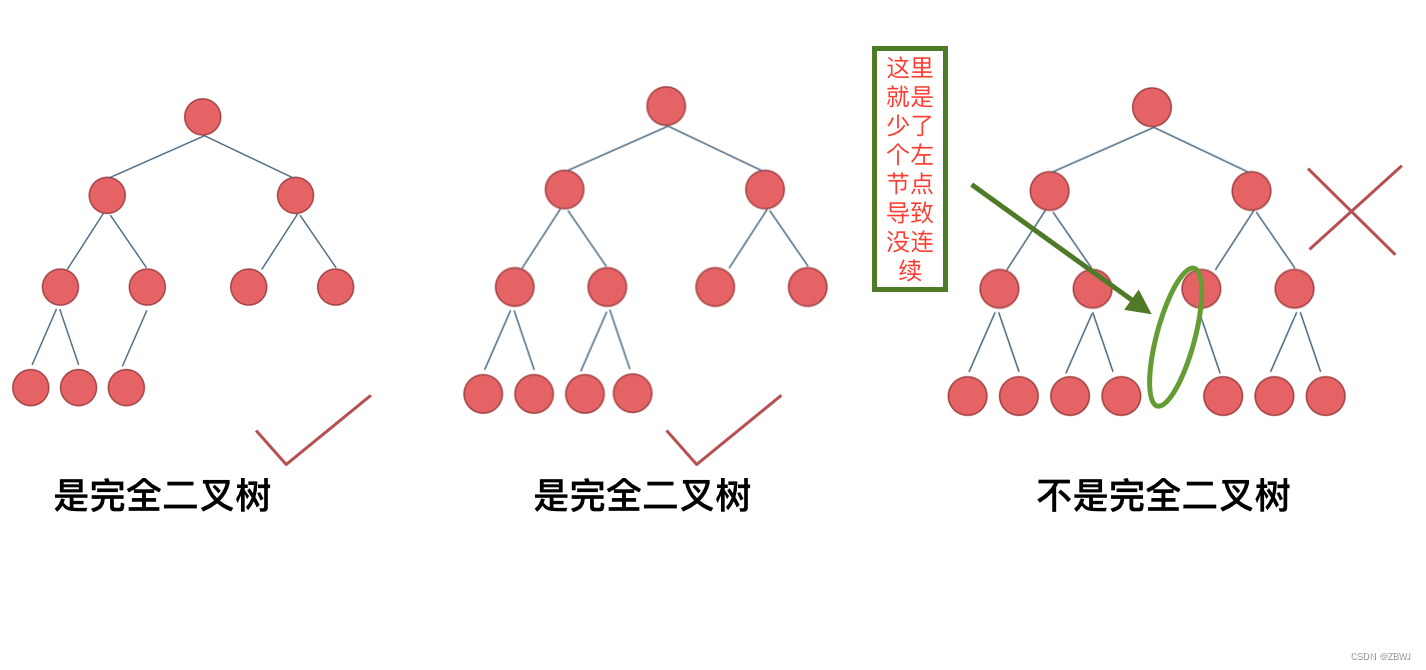
注: 优先级队列其实是一个堆,堆就是一棵完全二叉树,同时保证父子节点的顺序关系。(昨天的题目 347找前 k 个高频元素, 我还不知道什么是堆,这里慢慢就学到了 )
平衡二叉搜索树
又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
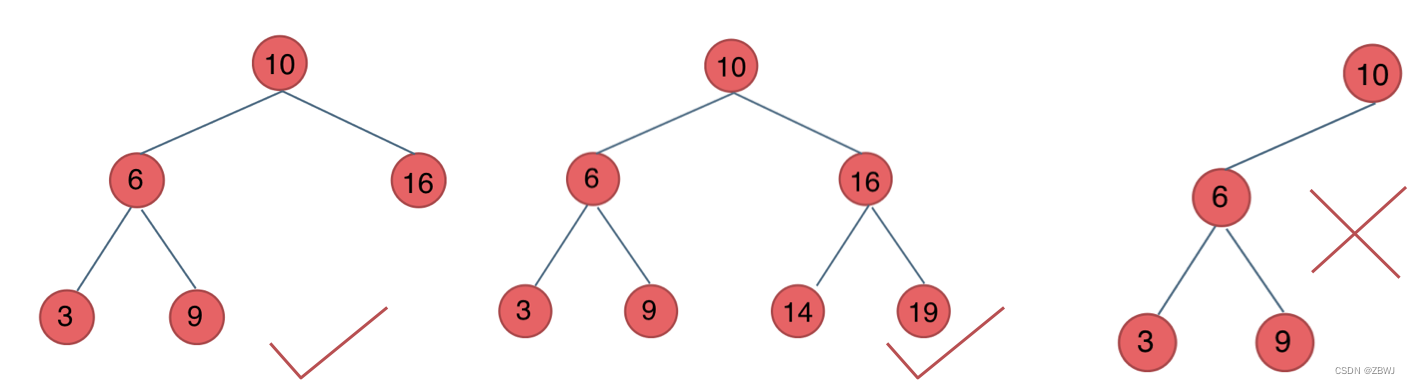
二叉树的存储方式
链式存储(指针)、顺序存储(数组) !
顾名思义就是顺序存储的元素在内存是连续分布的,而链式存储则是通过指针把分布在各个地址的节点串联一起。
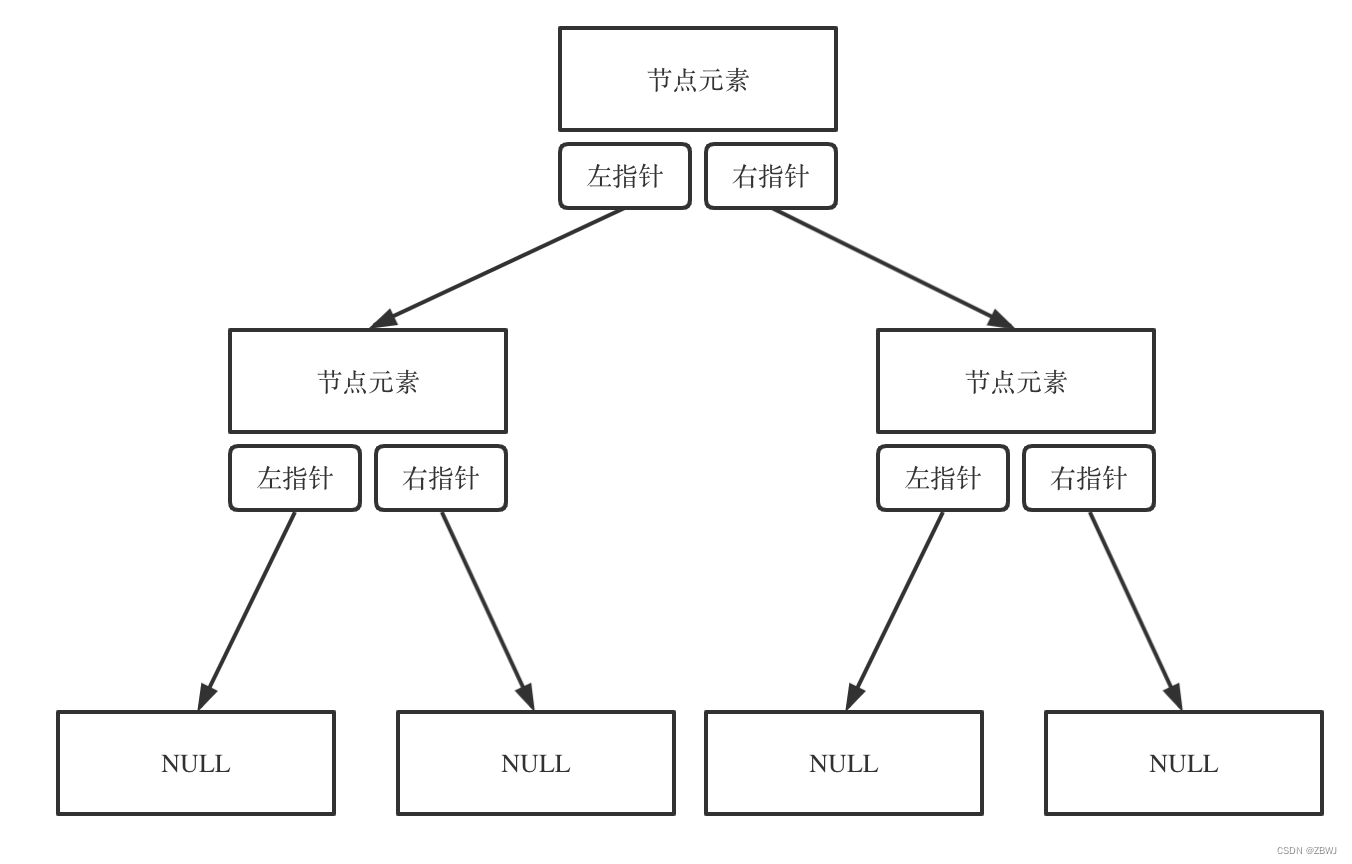
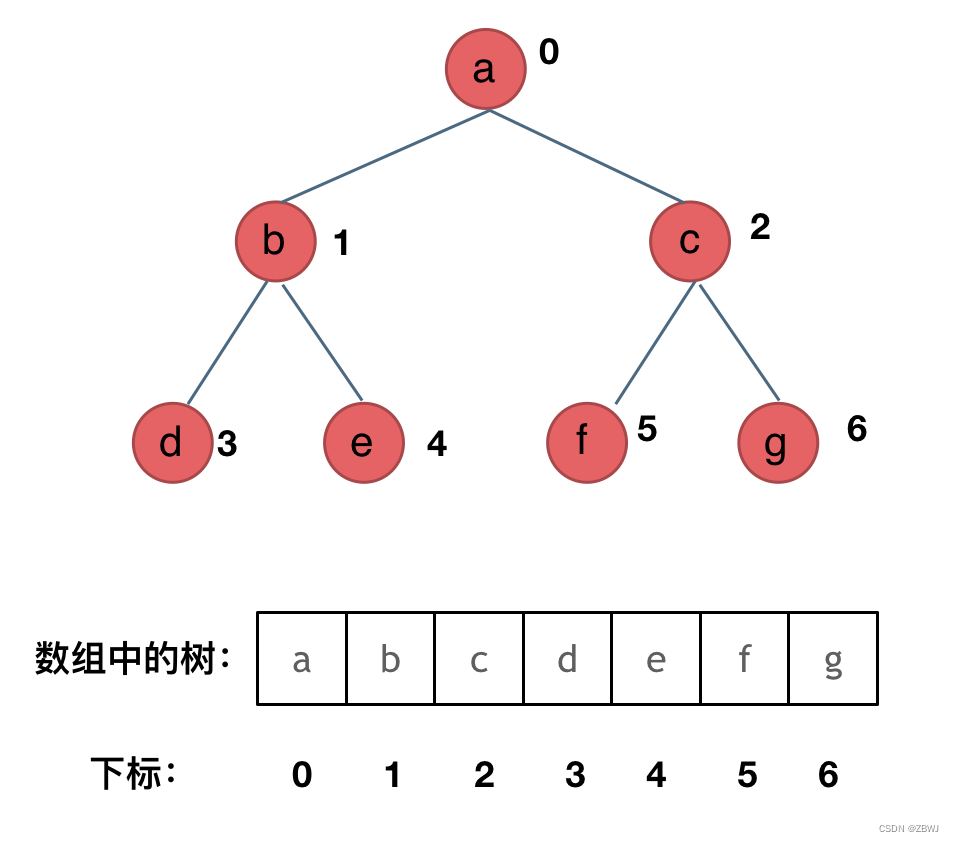
二叉树的数组如何遍历呢, 如果如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。例如 “父1 左3 右4”
二叉树的遍历方式
主要有两种遍历方式:
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层的去遍历
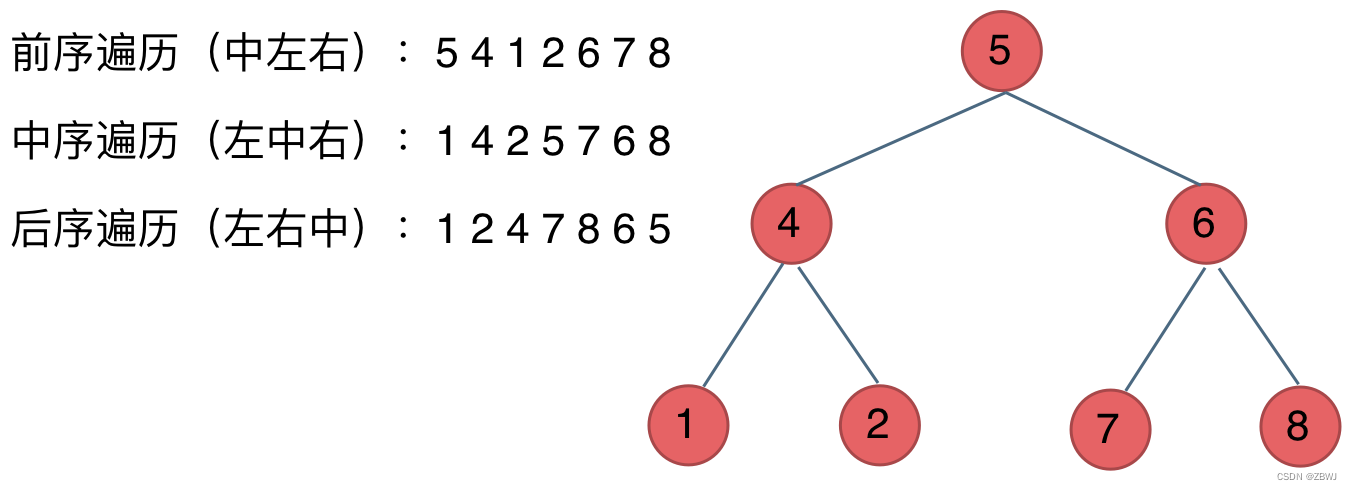
深度优先遍历
- 前序遍历(递归法,迭代法) 中左右
- 中序遍历(递归法,迭代法) 左中右
- 后序遍历(递归法,迭代法) 左右中
这里前中后,其实指的就是中间节点的遍历顺序,记住 前中后序指的就是中间节点的位置就可以了。
广度优先遍历
- 层次遍历(迭代法)
二叉树的实现方式
二叉树中深度优先和广度优先遍历实现方式,我们做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的。
栈其实就是递归的一种实现结构,也就说前中后序遍历的逻辑其实都是可以借助栈使用递归的方式来实现的。
而广度优先遍历的实现一般使用队列来实现,这也是队列先进先出的特点所决定的,因为需要先进先出的结构,才能一层一层的来遍历二叉树。
了解完理论基础, 下面开始搞题做了, 下篇见~
注: 以上内容参考自-- 代码随想录