目录
线性回归模型
问题
过程
模型f的选择
回归和分类比较
机器学习术语
模型训练
成本函数
介绍
设计成本函数
直观化理解成本函数
线性回归模型
问题
已知一系列房子的大小以及其对应的价格的数据,要求是已知房子大小预测其房子的价格
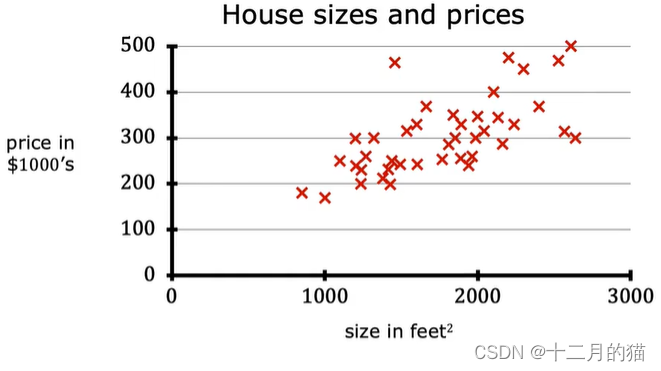
过程
一、根据已知的房子大小以及其对应的价格数据,画出上图所示的二维散点图
二、根据数据拟合一条直线,让其最接近数据样本,如下图
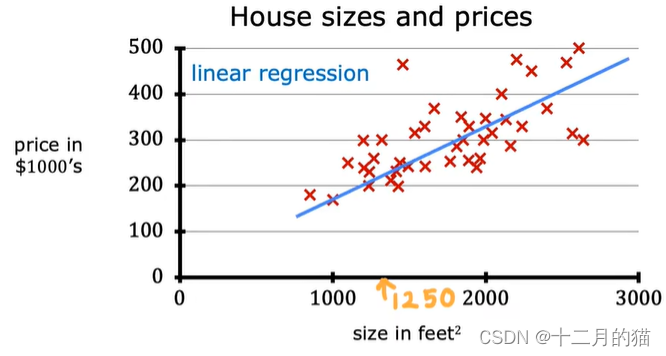
三、根据拟合出来的直线,将房子大小代入式子,便可预测房子的价格
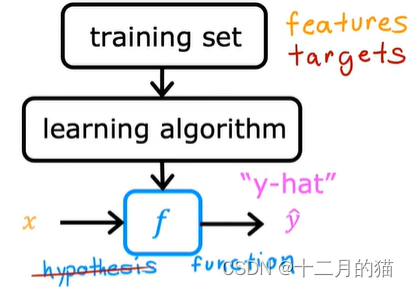
注意:
1、y-hat:利用模型求出的预测值
2、y:训练集中的真实值
3、x:待预测的变量
4、f:训练出来的模型
模型f的选择
在线性回归中,我们选择线性函数来作为训练模型如:
简写为:
该模型也称为:单变量线性回归(最基础的回归模型)
回归和分类比较
1、回归模型可以有无穷多个输出,分类模型的输出值个数是少量且固定的
2、分类模型和回归模型都是监督模型
3、分类模型是特殊的回归模型
机器学习术语
训练集:用来训练模型的数据

模型训练
在得到已知数据并构造散点图后,我们下一步要做的就是在数据中拟合直线。如何知道拟合的直线效果好不好呢?这个时候就要引入成本函数
通过比较不同直线在已知训练数据中成本函数值的大小就可以判断该直线拟合的效果如何
成本函数
介绍
成本函数(损失函数)是衡量模型预测结果与真实标签之间差异的函数
以下是两者的详细介绍:
- 损失函数(Loss Function):它计算的是单个样本的真实值与预测值之间的误差。在机器学习中,损失函数用于评估模型对于单个数据点的预测性能,常见的损失函数包括平均平方误差、交叉熵损失等。
- 成本函数(Cost Function):它是在所有训练样本上定义的,通常是指所有样本上的损失函数之和或平均值。成本函数衡量的是整个模型在全部数据集上的表现,通过最小化成本函数来寻找模型参数的最优解。
设计成本函数
1、损失函数就是衡量直线拟合的如何——》拟合好不好就是看预测值和真实值差距大不大
2、得到损失函数:——》考虑差值有正有负,将损失函数修改为:
3、衡量模型在整合训练集中的误差——》损失函数修改为:(m为训练集数量)
4、考虑到评估训练模型的好坏(客观的量,不受训练集大小影响)——》损失函数修改为:——》方便后续计算再次修改损失函数为:
5、将损失函数正式命名为
上面构造出来的成本函数称为:均方误差(MSE)
直观化理解成本函数
成本函数:是一个关于w,b两个参数的变量
模型f:是一个关于x的变量
当选定一个w,b就能构造一个模型f,同时计算出模型f的成本函数的值,从而在成本函数图像中确定一个点。当选择更多的w,b时就能画出成本函数的函数图像
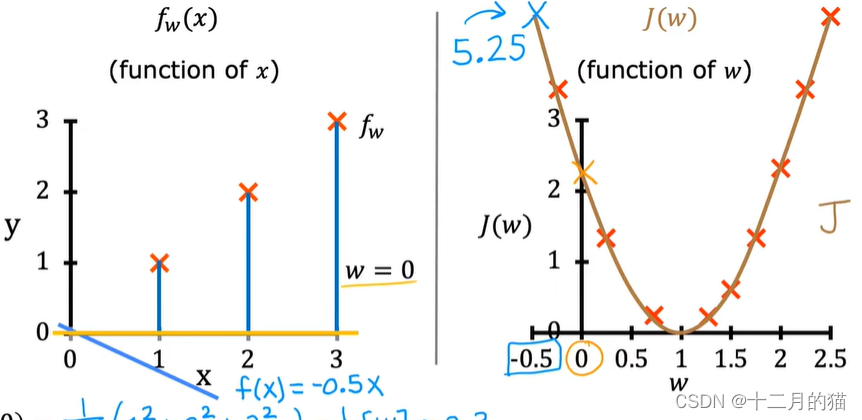
右图:由每一个参数对应的成本函数值,画出的成本函数的函数图