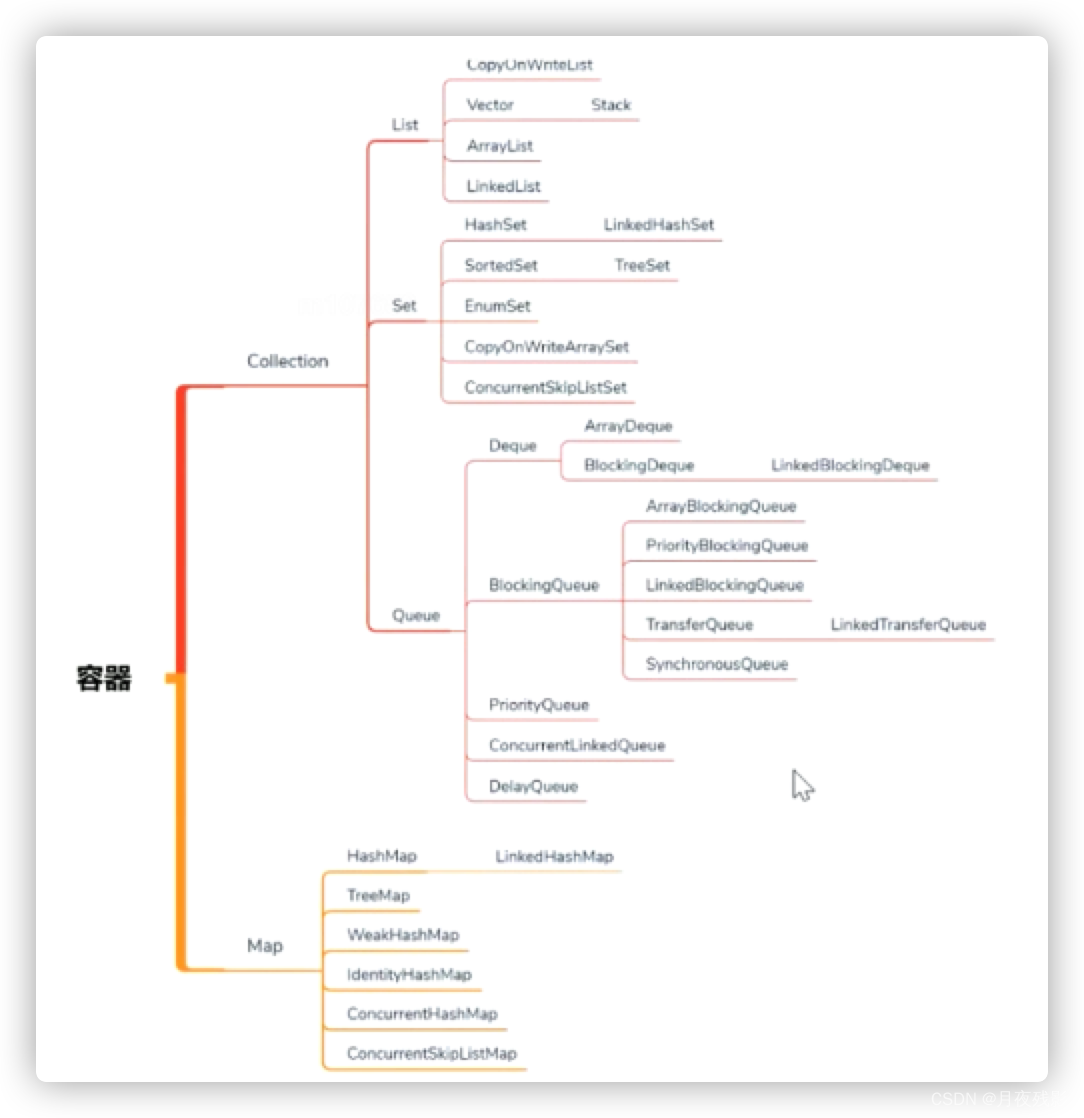
目录
错排算法
三维数组的应用
错排算法
发邮件__牛客网
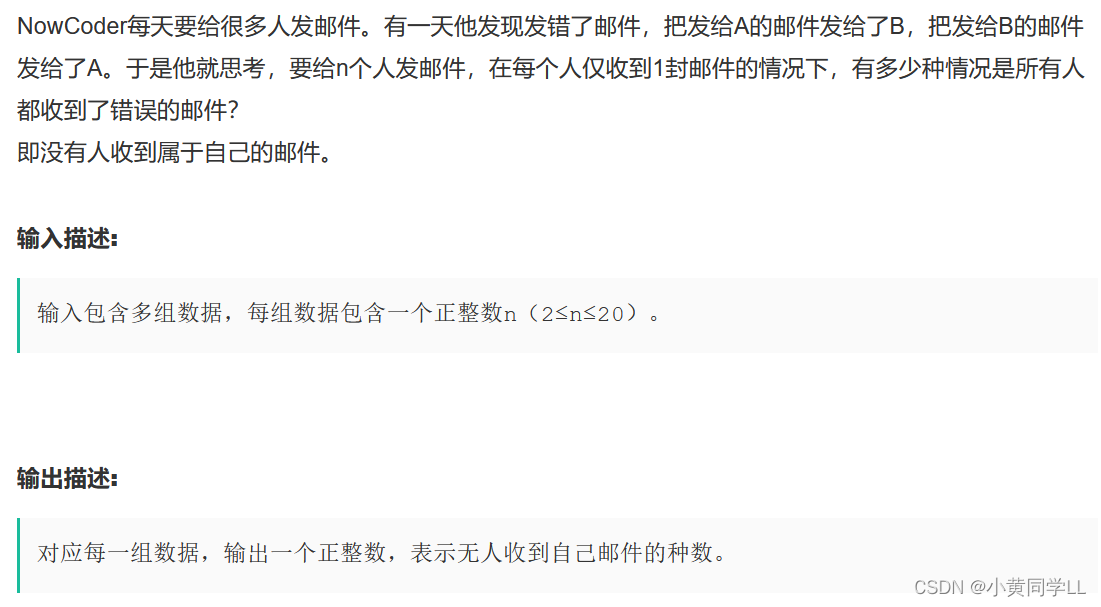
错排:
假设有n封信要装入到n个信封中,每封信应该要放到对应的信封中,比如:信: A B C D...
信封: a b c d. ...
由于疏忽将信放置出错,总共有多少种可能性每封信都放错假设:D(n)表示n封信总共装错的总数
如果A装入到b的信封中:
- 将B信装入到A的信封中(a、b互相放错形成独立): A-->b B-->a出错的总数:取决于剩余的n-2封信: D(n-2)
- 将B信装入到除A以外的其他信封(只有A与b完成独立):剩余n-1封信放错的可能性为D(n-1)
所以A装错到b的信封后有D(n-1) +D(n-2)种出错数
同理,如果将A装入到C、D、E (n-2)*(D(n-1)+D(n-2));总的出错总数:(n-1)*(D(n-1)+D(n-2));
特殊的:
如果是0封信:D(0)--->0
如果是1封信:D(1)--->0
如果是2封信: D(2)--->1
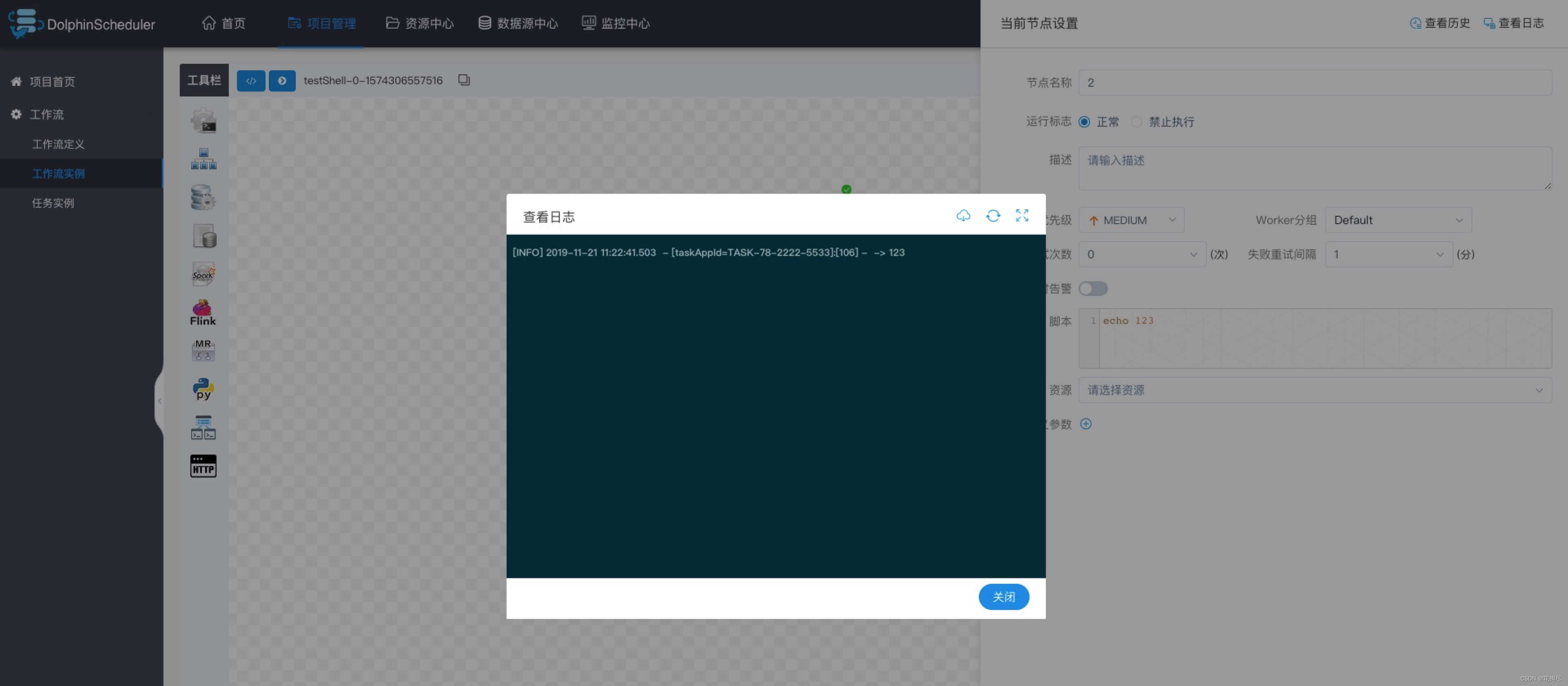
#include<iostream>
using namespace std;
int main()
{
long long d[21]={0,0,1};
for(int i=3;i<=20;i++)
{
d[i]=(i-1)*(d[i-1]+d[i-2]);
}
int n;
while(cin>>n)
cout<<d[n]<<endl;
return 0;
}三维数组的应用
五子棋__牛客网
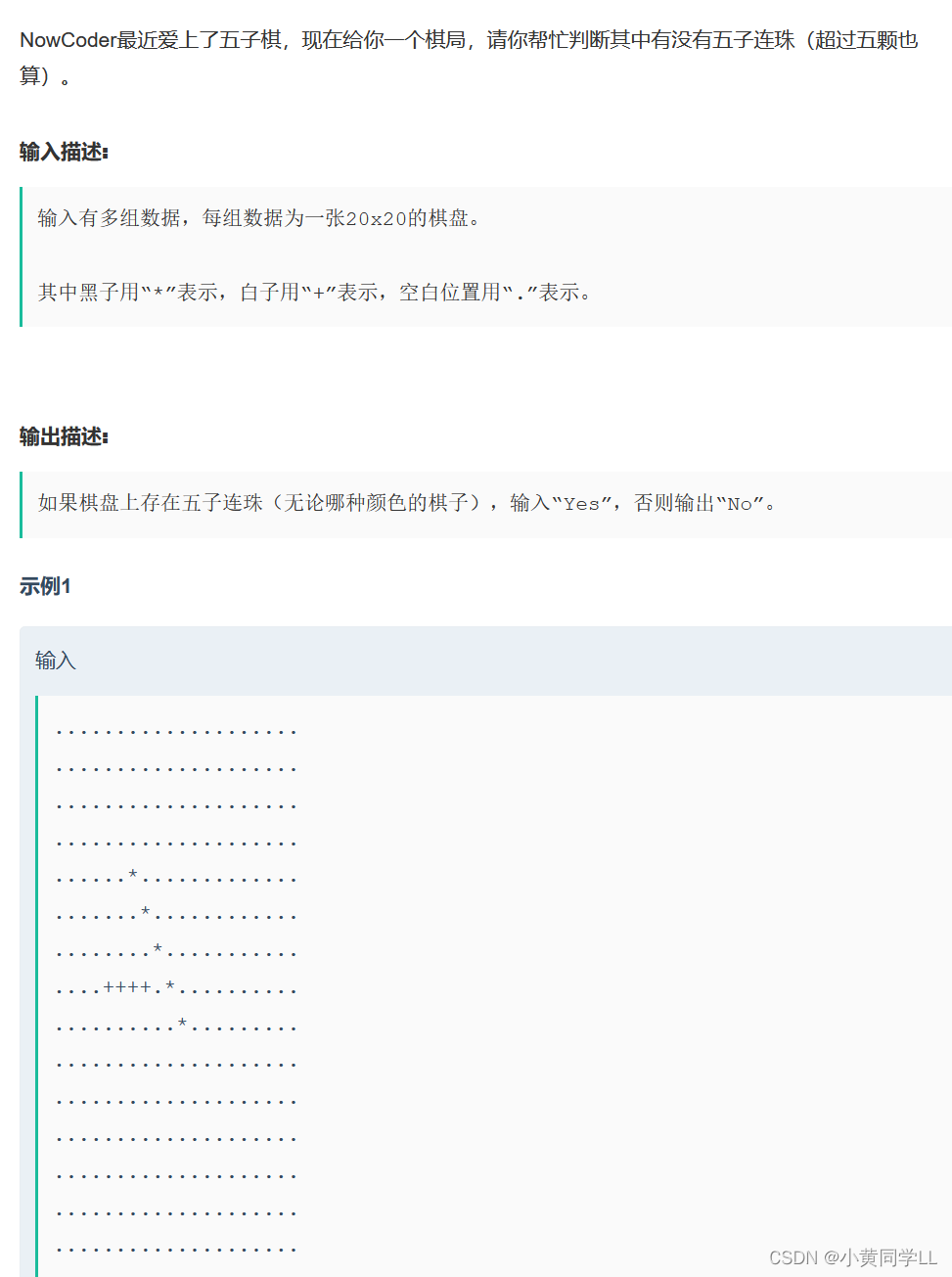
核心在于构建三维数组以遍历方向;
int d[横竖斜线][两个小方向][坐标x,y]={ {{x1,y1},{x2,x2}},{...},{},{} }
可以理解为二维数组里面存数组,例如 int a[][]={ {【数组】},{...},{} }
#include <iostream>
#include <fstream>
#include <string>
using namespace std;
#define N 20
int count(string table[], char ch, int x, int y)
{
int maxc = 0;
int dir[4][2][2] = { {{ -1,0 },{ 1,0 }},
{{ 0,-1 },{ 0,1 }},
{{ -1,-1 },{1,1 }},
{{ -1,1 },{ 1,-1 }} };
for (int i = 0; i < 4; ++i) // 四种方向
{
int c = 0;
for (int j = 0; j < 2; ++j) // 两个小方向
{
int nx = x, ny = y;
while (nx >= 0 && nx < N && ny >= 0 && ny < N && table[nx][ny] ==ch)
{
nx += dir[i][j][0];
ny += dir[i][j][1];
++c;
}
}
maxc = max(maxc,c);
}
return maxc - 1; //统计两个方向(如横向的左右两个方向)的时候,
//当前棋子被计算了两次
}
bool solve(string table[])
{
// 遍历棋谱,如果某个位置有棋子,再想该位置进行搜索
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
{
if (table[i][j] == '*' || table[i][j] == '+')
// 当某个位置有连在一起的棋子,结束搜索
if (count(table, table[i][j], i, j) >= 5)
return true;
}
}
return false;
}
int main()
{
string table[N];
while (cin >> table[0])
{
for (int i = 1; i < N; ++i)
cin >> table[i];
cout << (solve(table) ? "Yes" : "No") << endl;
}
return 0;
}