1.算术逻辑单元(ALU)
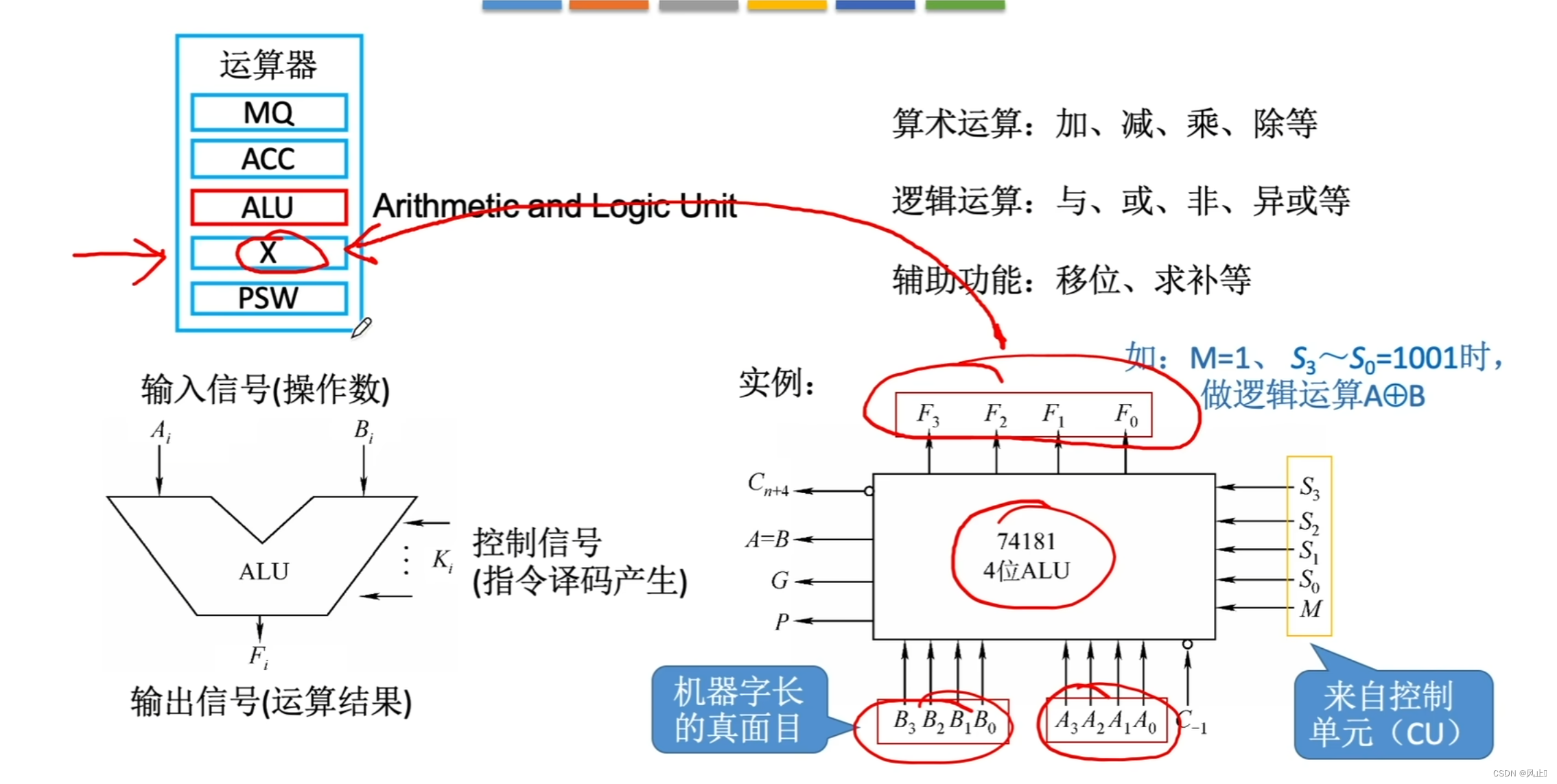
输入信号:A和B为要进行计算的两个操作数。(本质上就是高低电频电信号)
输出信号:输出运算结果
控制信号:由控制单元(CU)发出,解析指令的含义,解析完发出控制信号,M表示做什么运算,M=1(逻辑运算) M=0(算术运算) S0 ~ S3指明是哪一种运算。
补充: 寄存器的位数就是机械字长,因为需要保存运算结果。
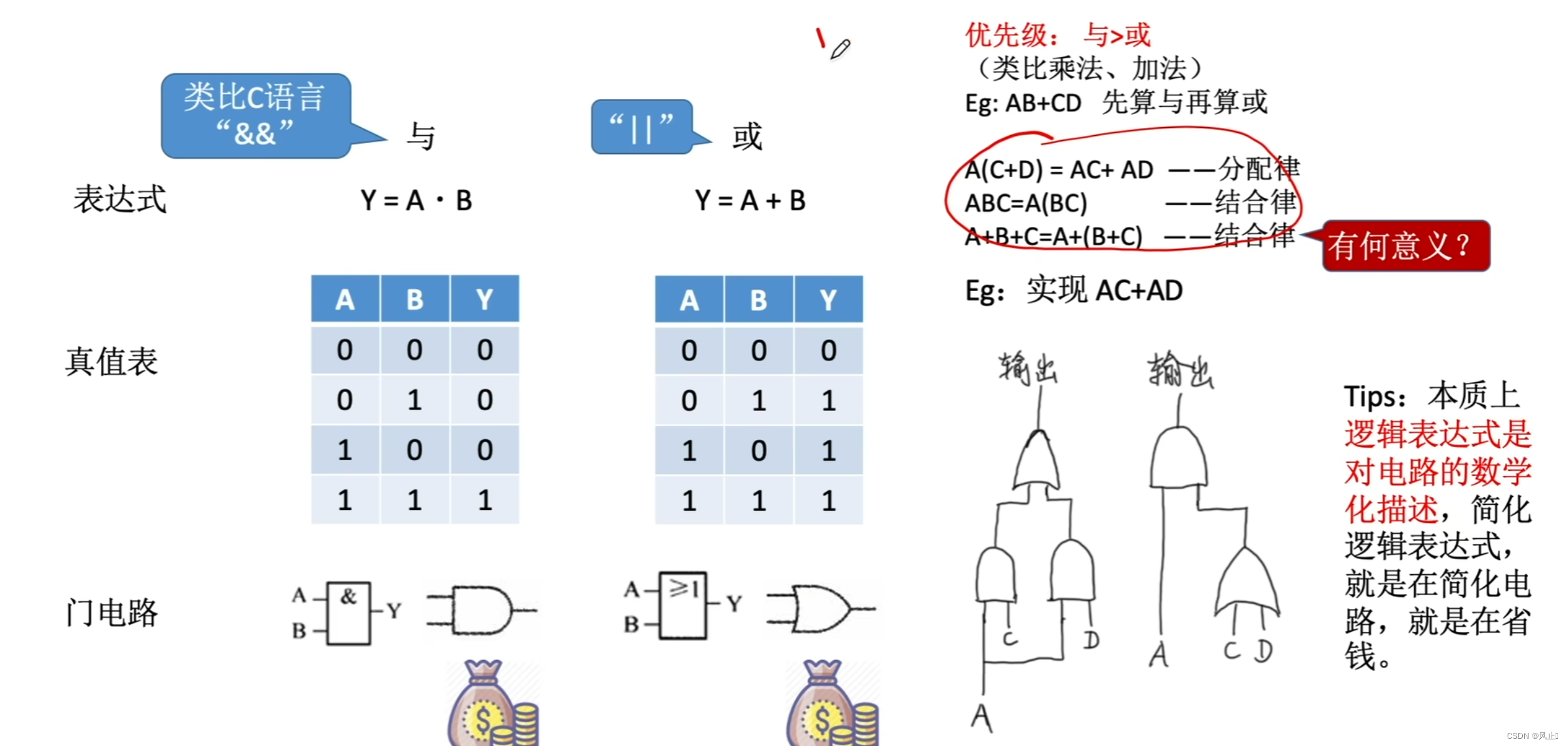
2.最基本的逻辑运算
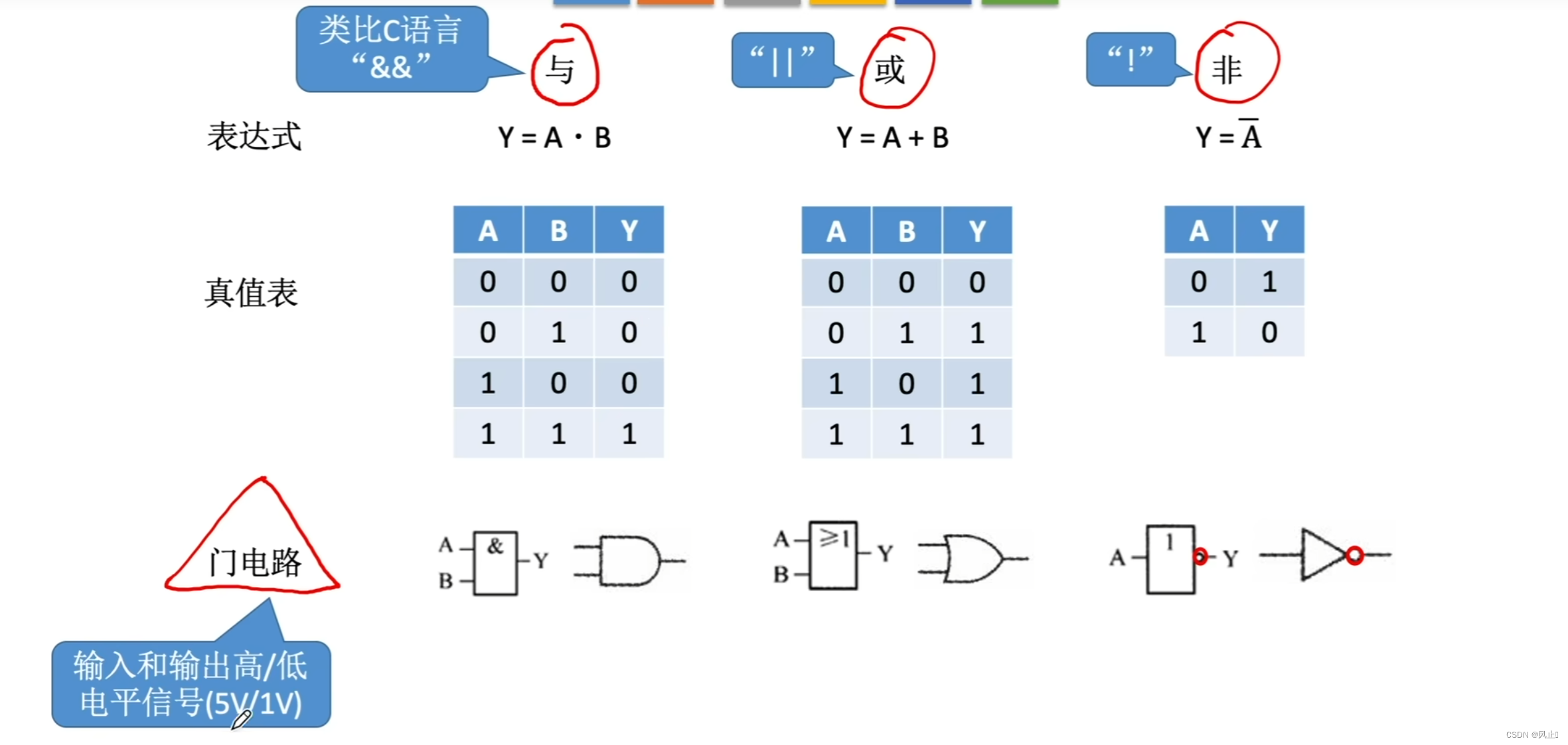
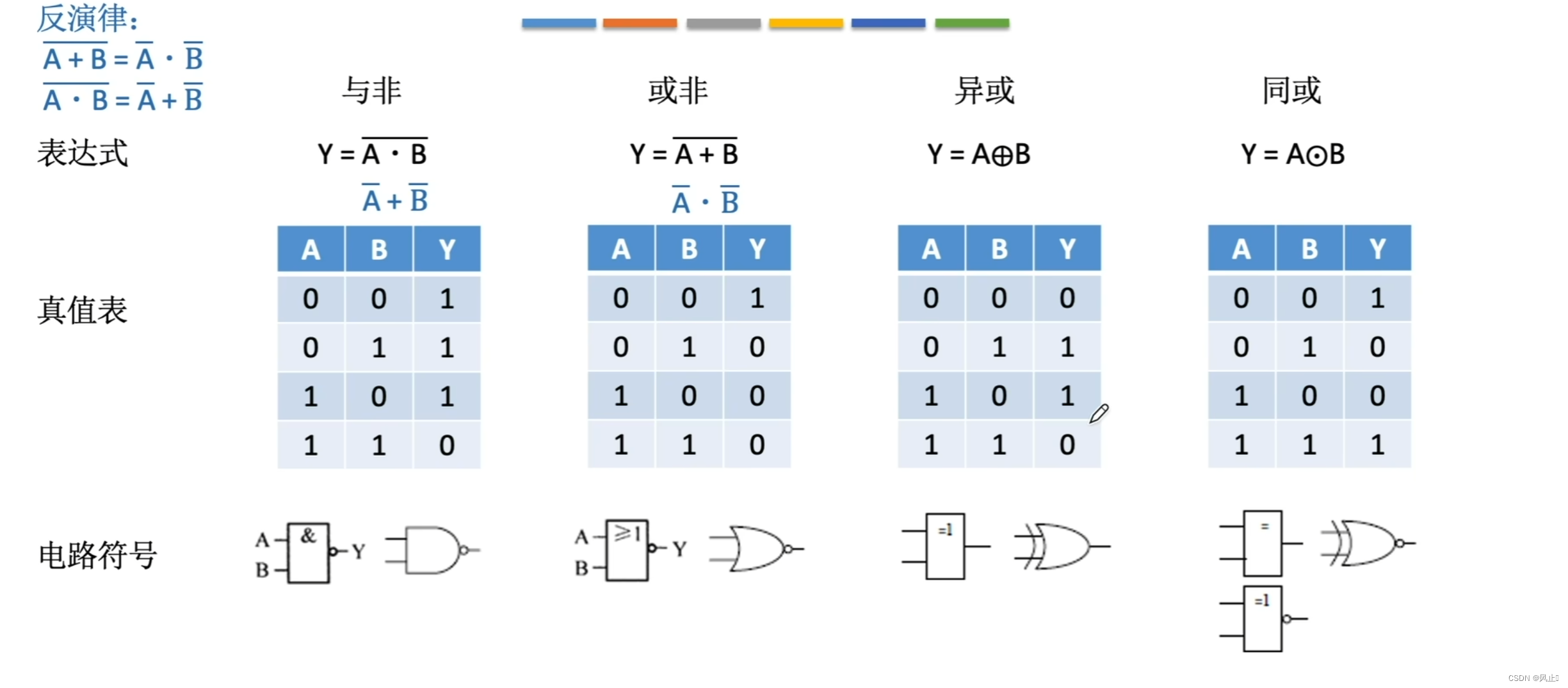
通过优先级,对设计电路优化,降低成本
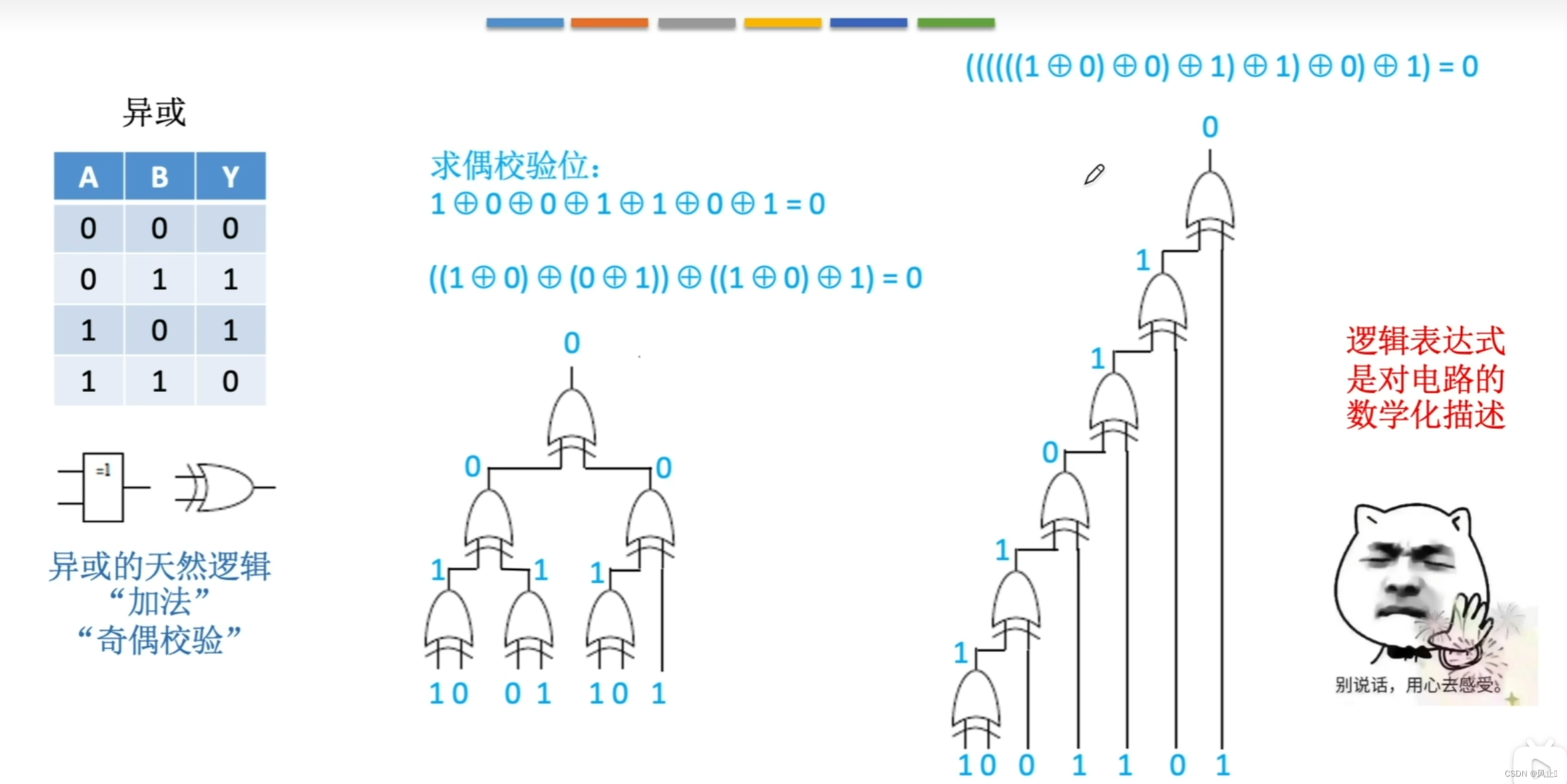
 3.使用门电路求奇偶校验位
3.使用门电路求奇偶校验位
 4.门电路实现加法运算
4.门电路实现加法运算
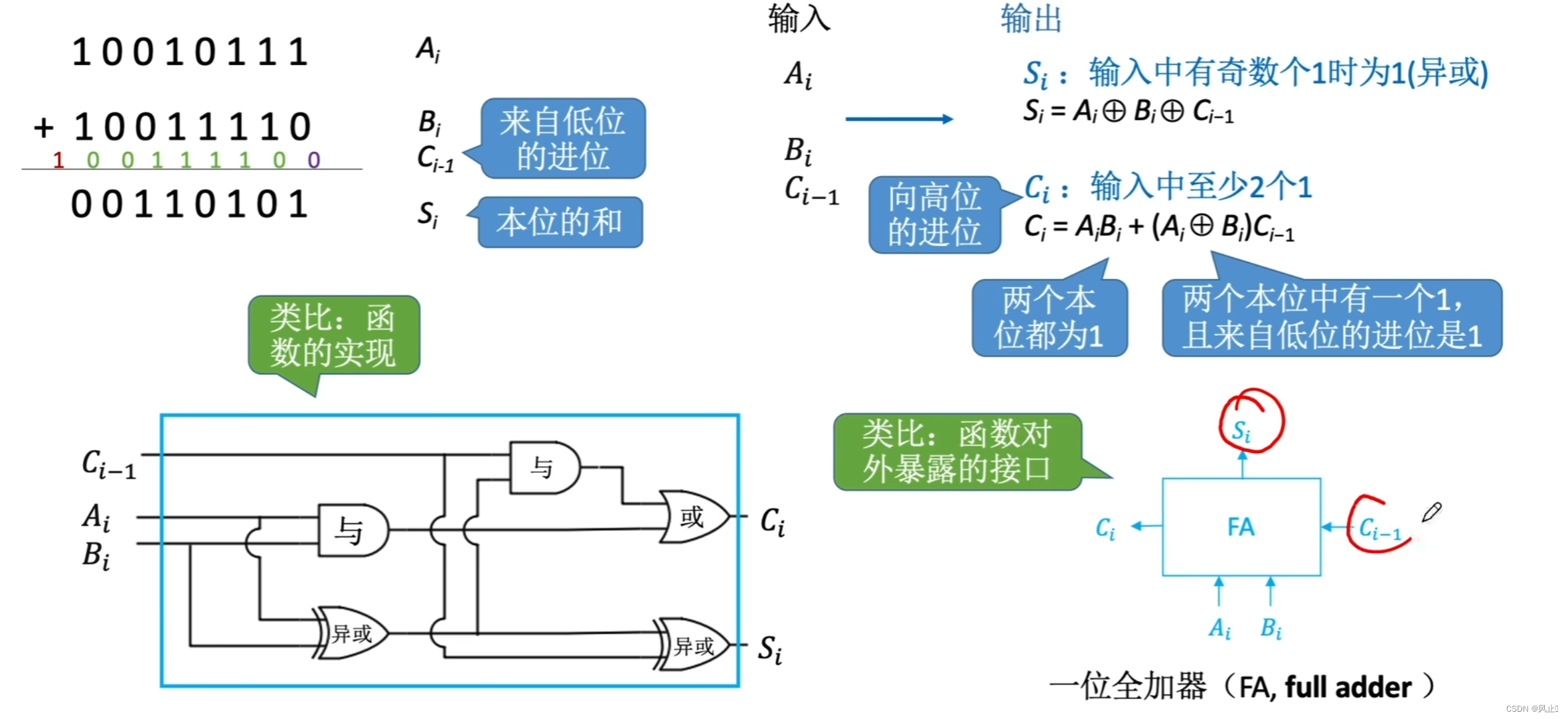
我们可以将上述思想联想乘 java实现的相加
public static int add(int a, int b) {
while (b != 0) {
// 计算进位
int carry = (a & b) << 1;
// 异或操作得到不考虑进位的和
a = a ^ b;
// 将进位赋值给b,继续循环直到进位为0
b = carry;
}
return a;
}上述代码就是并行加法器,同时计算,算出进位在同时计算,没有进位了,结束计算。
串行加法器
成本比较低,复杂度比较低。
电路简单使用与低消耗和低速度要求的应用。
这种方法一位一位的相加,每次A B输入二进制的一个数,然后进行相加,在将进位存到进位触发器里面,这样操作数有几个字节就需要进行对应字节*8的计算,这样的效率是比较低的。

串行进位的并行加法器
这种思想,可以同时处理所有位,计算的速度取决于进位的速度,跟串行比,如果不需要进位,就不需要计算了,但这种效率也不高,它的效率取决于每位进位的效率。
主要优点:是速度快,特别适用于需要高速计算的应用,比如数字信号处理。图形处理。
但这种设计方式电路复杂度比较高,成本比较高。
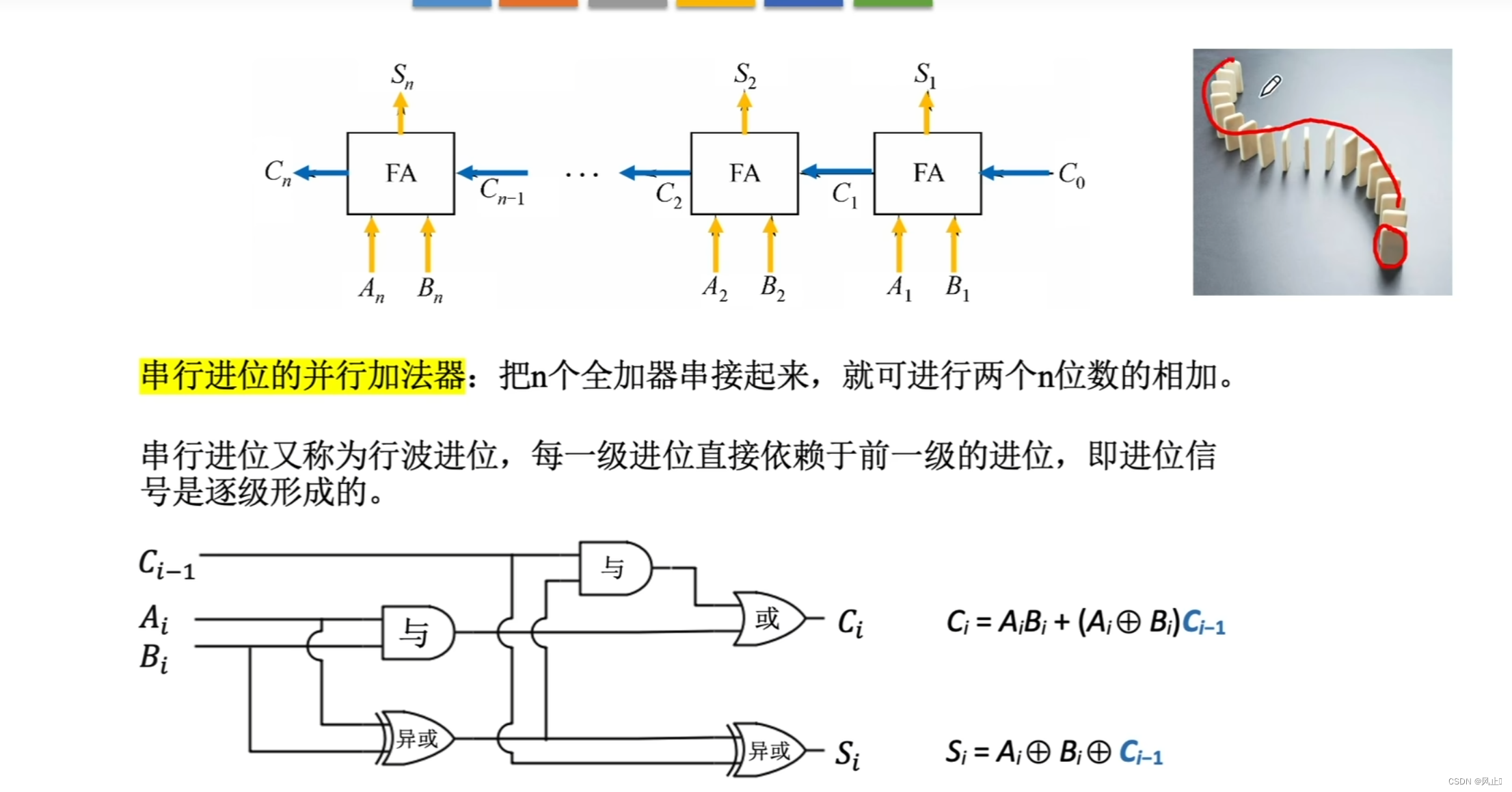
对上述加法器的优化,就是让进位的速度产生的更快。

这样就以递归的思想求出每一位进位的值,就不需要每一次都等待上一次的结果进行了。
并行进位的并行加法器
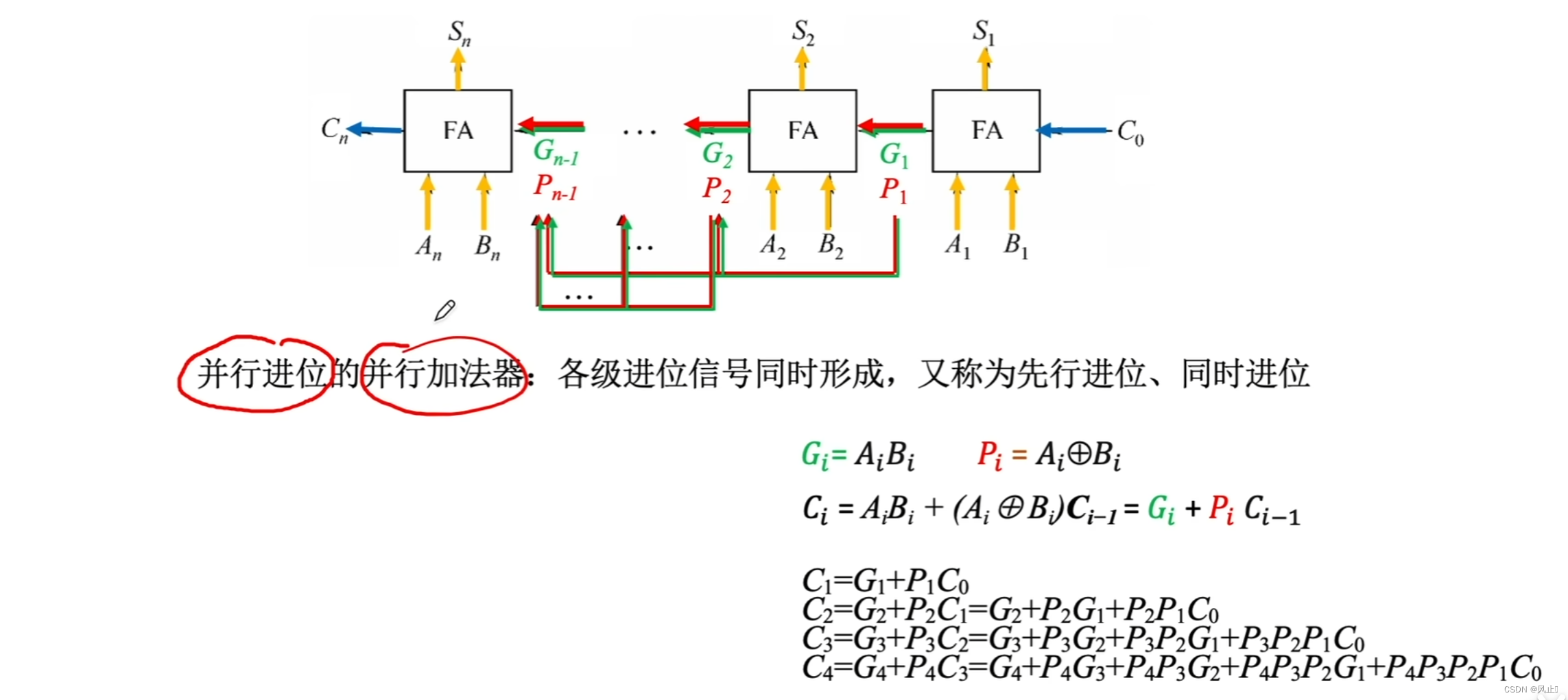 但是这种也会存在一些不足,因为随着我们继续套娃,逻辑表达式越来越复杂,又因为逻辑表达式本质上就是电路的一种数学化的描述,所以电路设计将越来越复杂。最好我们就套娃到C4让我们最多支持四位加四位的运算。
但是这种也会存在一些不足,因为随着我们继续套娃,逻辑表达式越来越复杂,又因为逻辑表达式本质上就是电路的一种数学化的描述,所以电路设计将越来越复杂。最好我们就套娃到C4让我们最多支持四位加四位的运算。
5.加法器原理

6.减法器原理
减法器的原理就是在加法器的基础上夹一个多路选择器如果输入的是1,表示减法,此时Cin会输入sub变为1 ,而y也会走1就是非门,就会全部按位取反(反码).
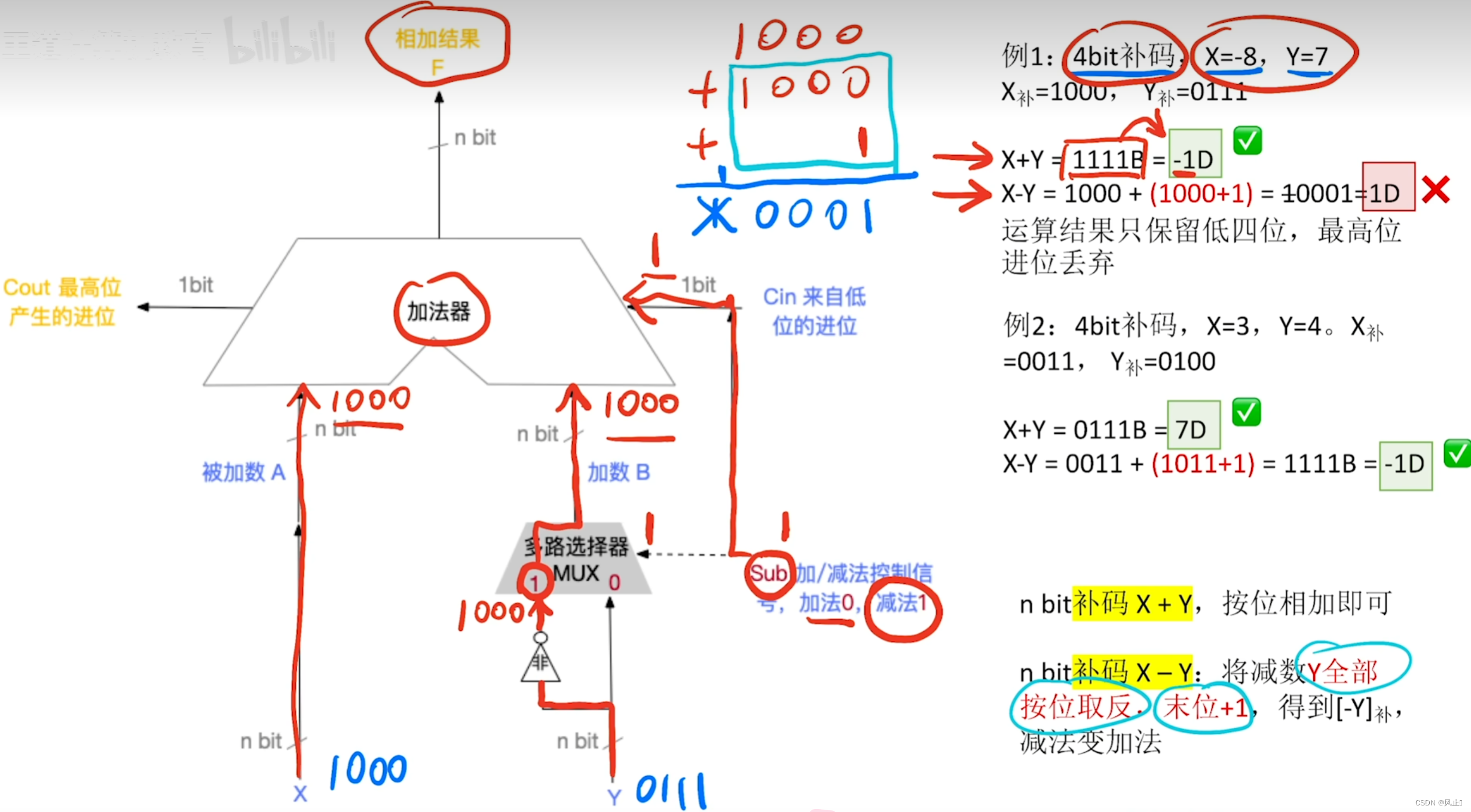
7.计算原理
原码计算原理
补码计算原理
补码只需要设置一个加法器即可。

溢出判断
当两个符号相同的数进行相加的时候就会发生溢出,溢出分为上溢和下溢。
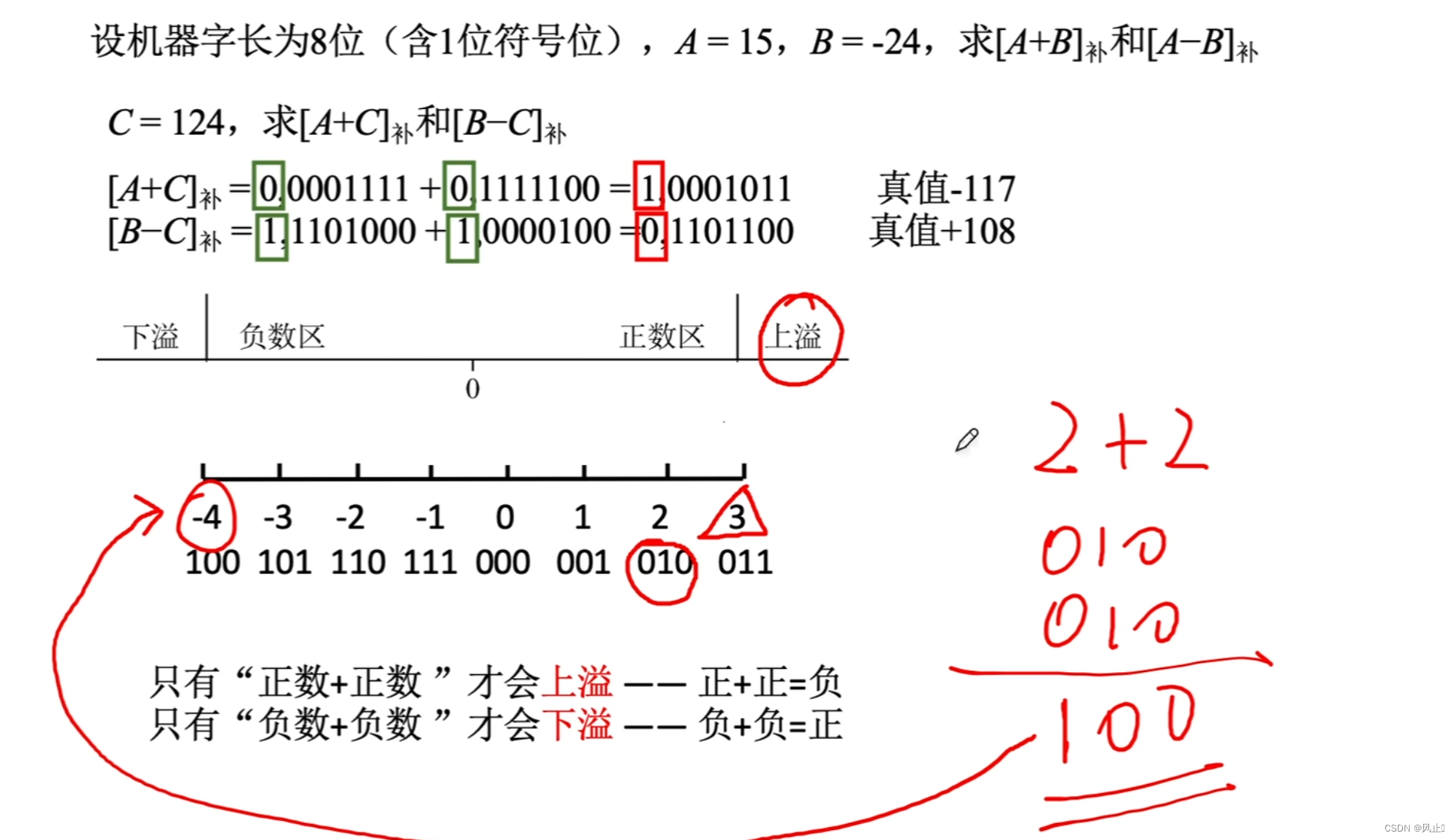 硬件判断溢出
硬件判断溢出

符号扩展

8.标志位的生成


9.算术移位
原码
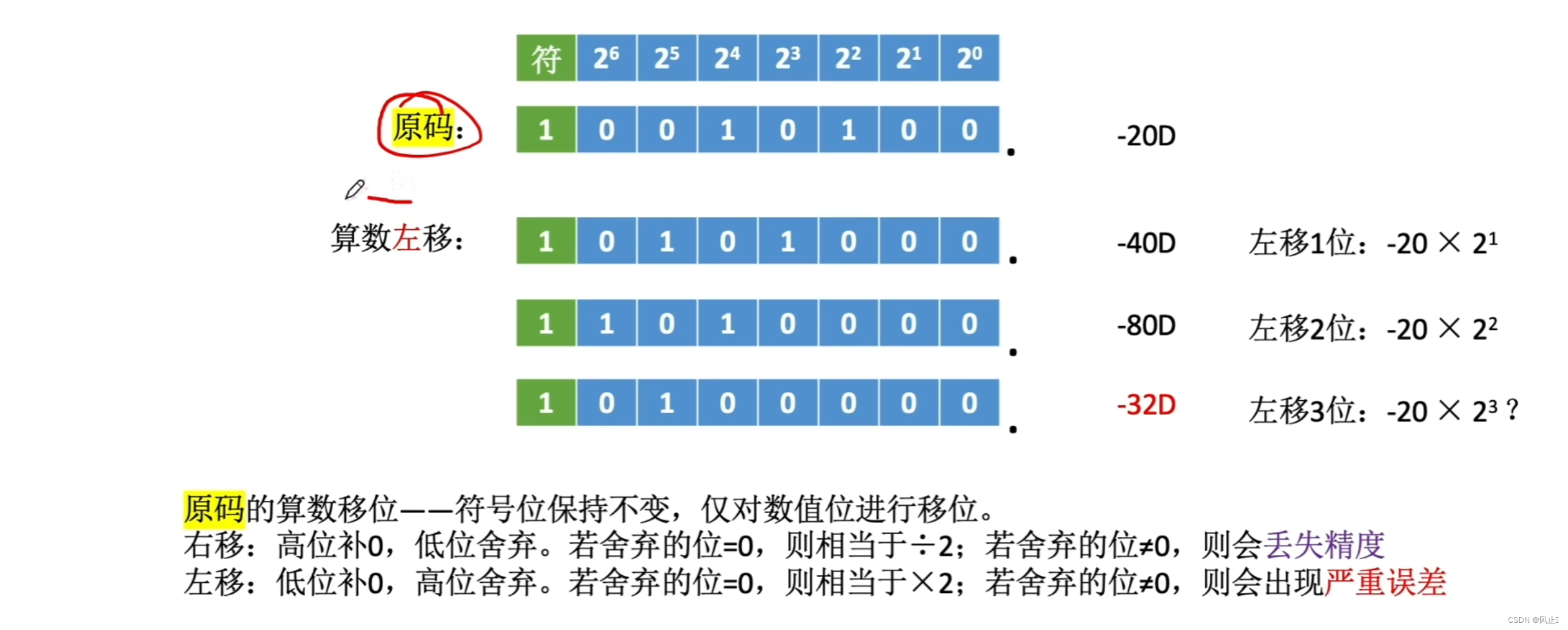 补码
补码

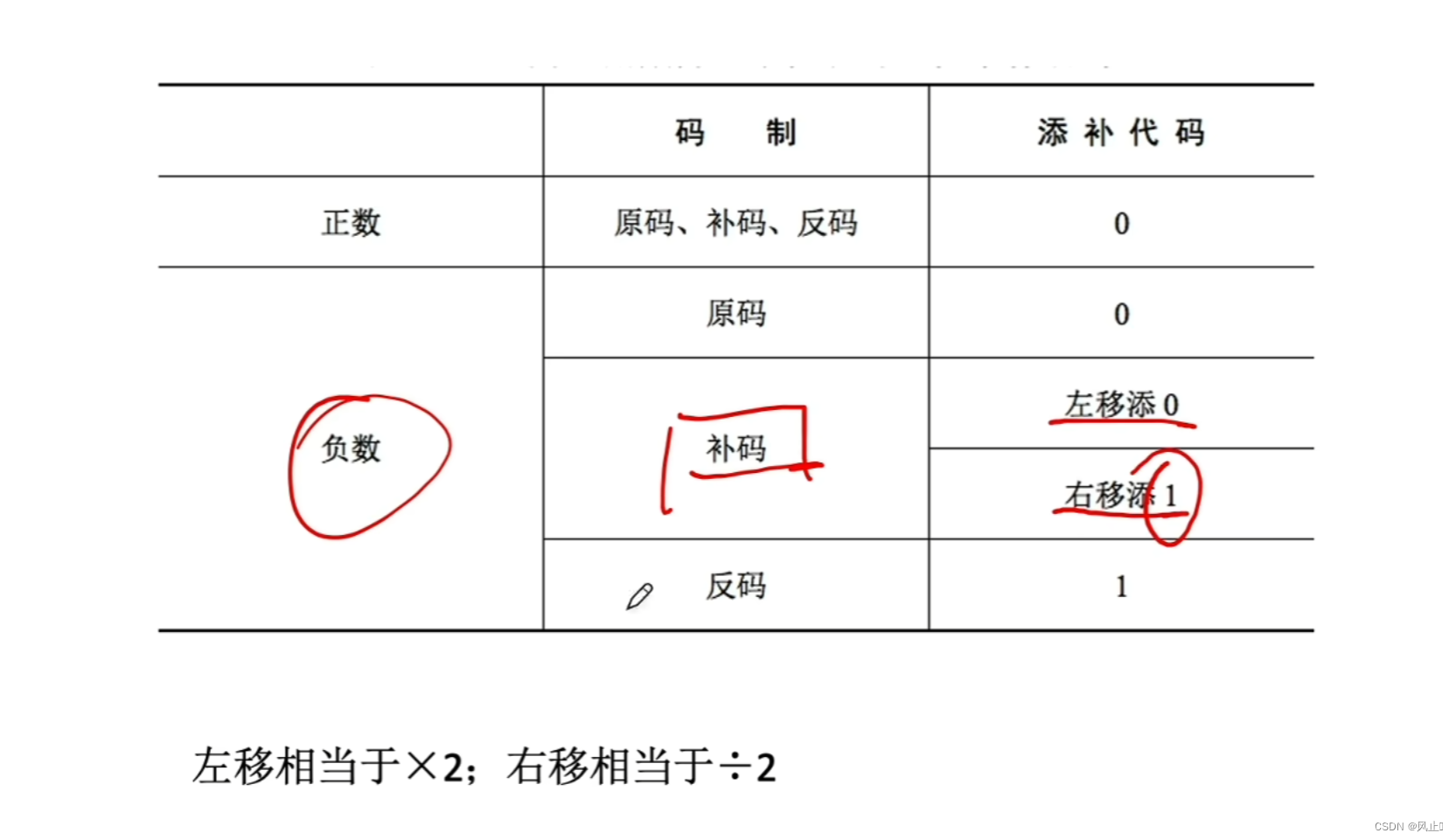
二进制怎么计算乘法的
实现乘法的原理就是:比如说计算20 * 7 = 20 * (2º + 2¹ + 2²) = 20 << 0 + 20 << 1 + 20 << 2
 硬件怎么实现的呢?
硬件怎么实现的呢?
使用ACC保存乘积的高位和MQ保存低位,然后让ACC和MQ成为一个整体统一右移,然后进行错位相加,循环此步骤,直到符号位移动到最后为止。然后再通过两个乘数的符号位异或来判读最终的答案是什么符号。

二进制怎么计算除法的
20 / 7 = 20 / (2º + 2¹ + 2²) = 20 >> 0 + 20 >> 1 + 20 >> 2
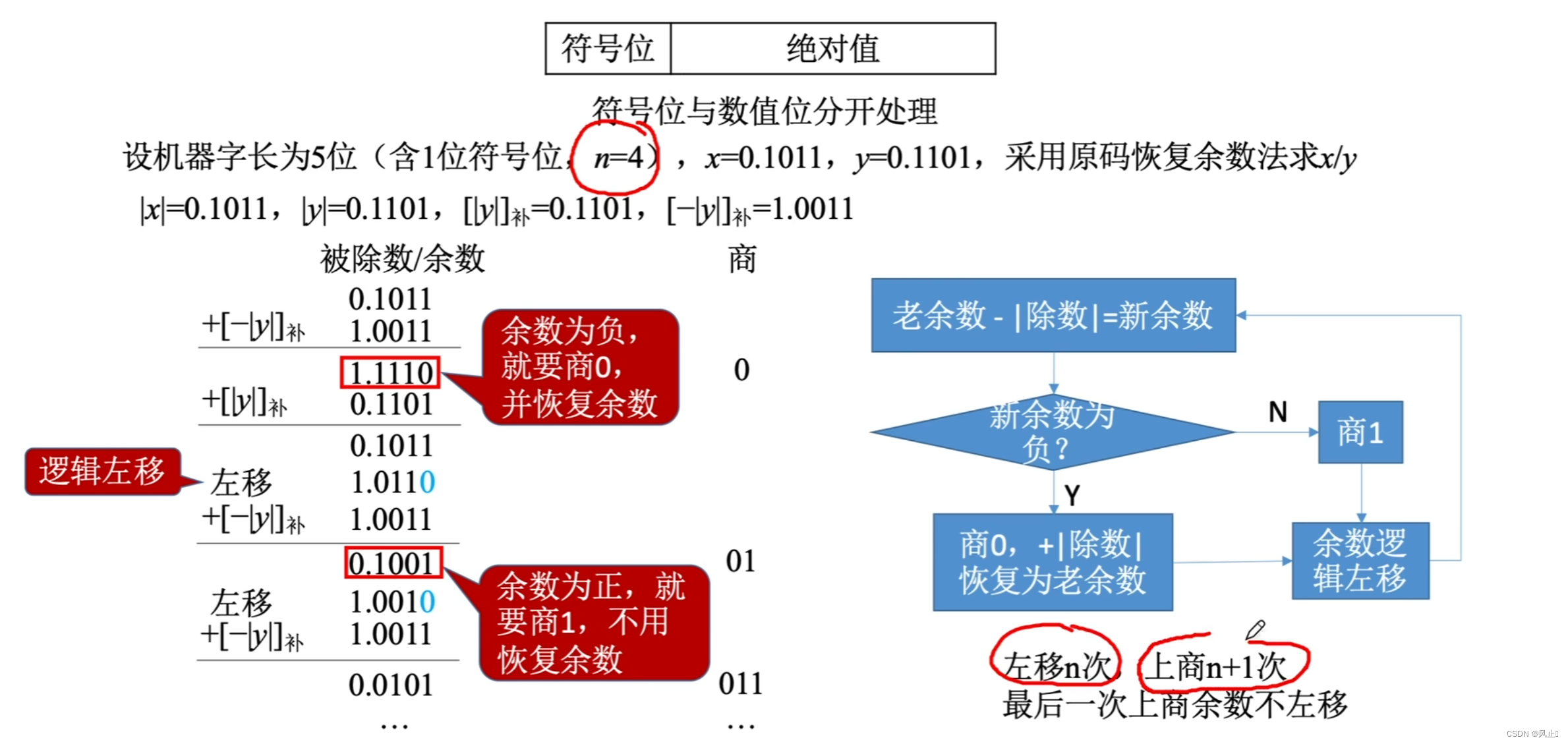
硬件怎么实现的呢?
原理就是: MQ保存商,ACC保存被除数和余数,默认商的最高位为1(因为计算机不知道是除数大还是被除数大)。然后使用除数 - 被除数(+(-被除数的补码)) ,发现结果为 负数(ACC中最高位为1),然后再+被除数恢复原样(恢复余数),然后商0,然后进行逻辑左移,依次计算即可。最后异或求符号位即可。
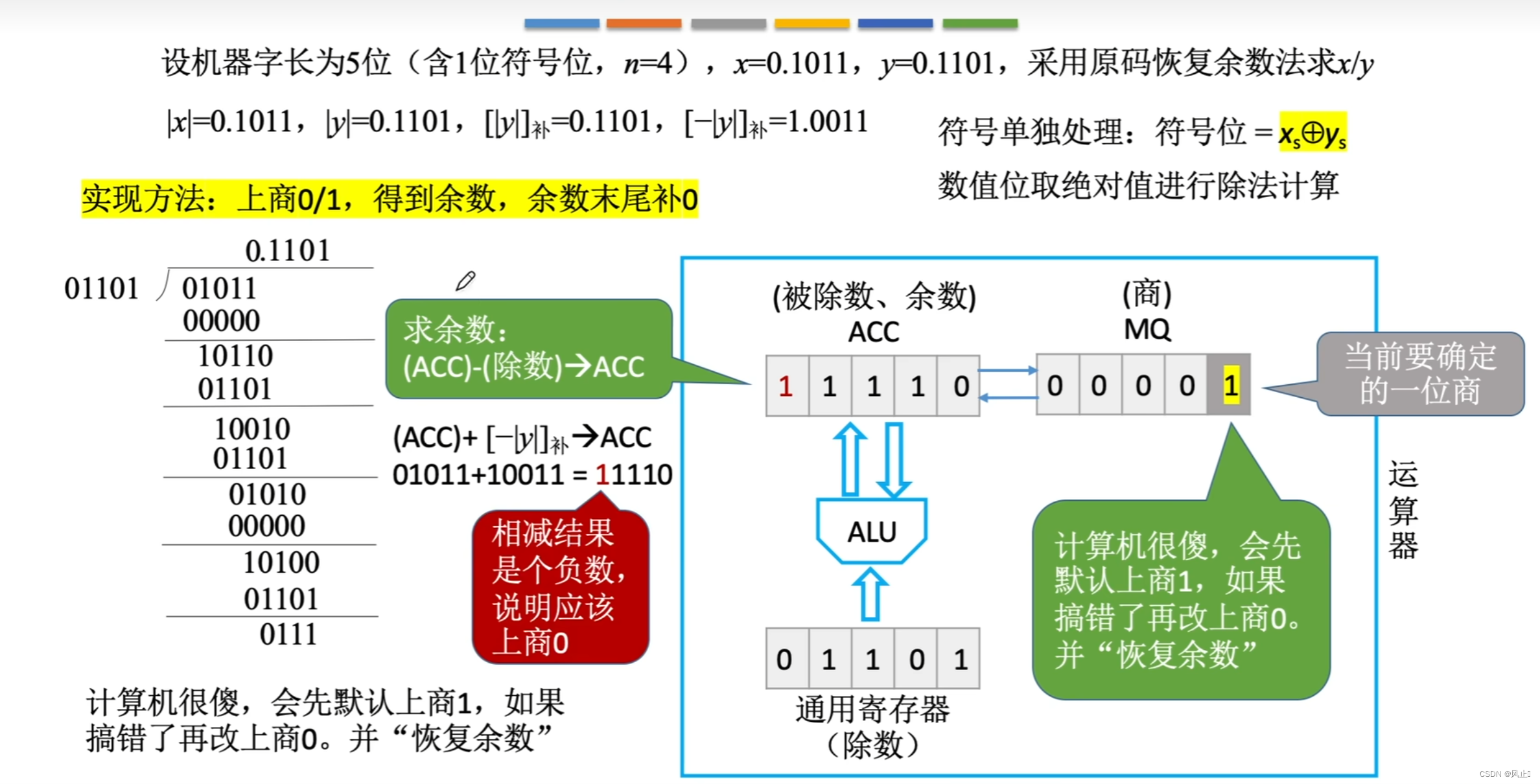
但是每次恢复余数效率就很低
我们可以进行不恢复余数,比如说 商1了我们知道结果为负数a,然后我们就商0,进行下次计算,下次计算余数右移一位 2a 然后再减去被除数b 本来是 a + b 右移动 2a + 2b 然后 2a +2b - b 现在我们不移动只需要 2 a 不减 + b即可


10.浮点数的表示
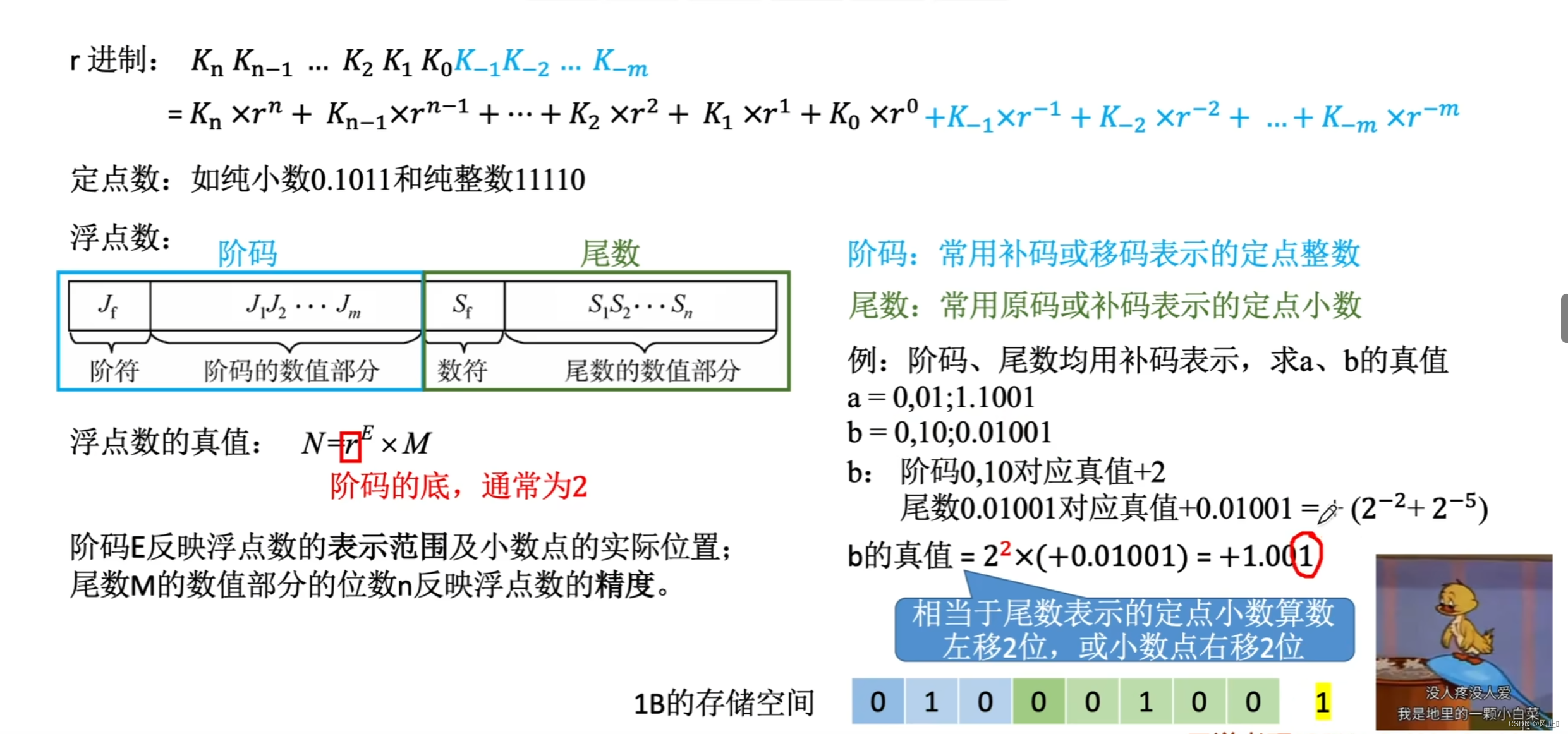

![[lesson39]逗号操作符的分析](https://img-blog.csdnimg.cn/direct/4592a6310d6d4a7caa61eb024f6b503c.png#pic_center)