491. 非递减子序列
思路:
在90.子集II (opens new window)中我们是通过排序,再加一个标记数组来达到去重的目的。
而本题求自增子序列,是不能对原数组进行排序的,排完序的数组都是自增子序列了。
所以不能使用之前的去重逻辑!
为了有鲜明的对比,我用[4, 7, 6, 7]这个数组来举例,抽象为树形结构如图:
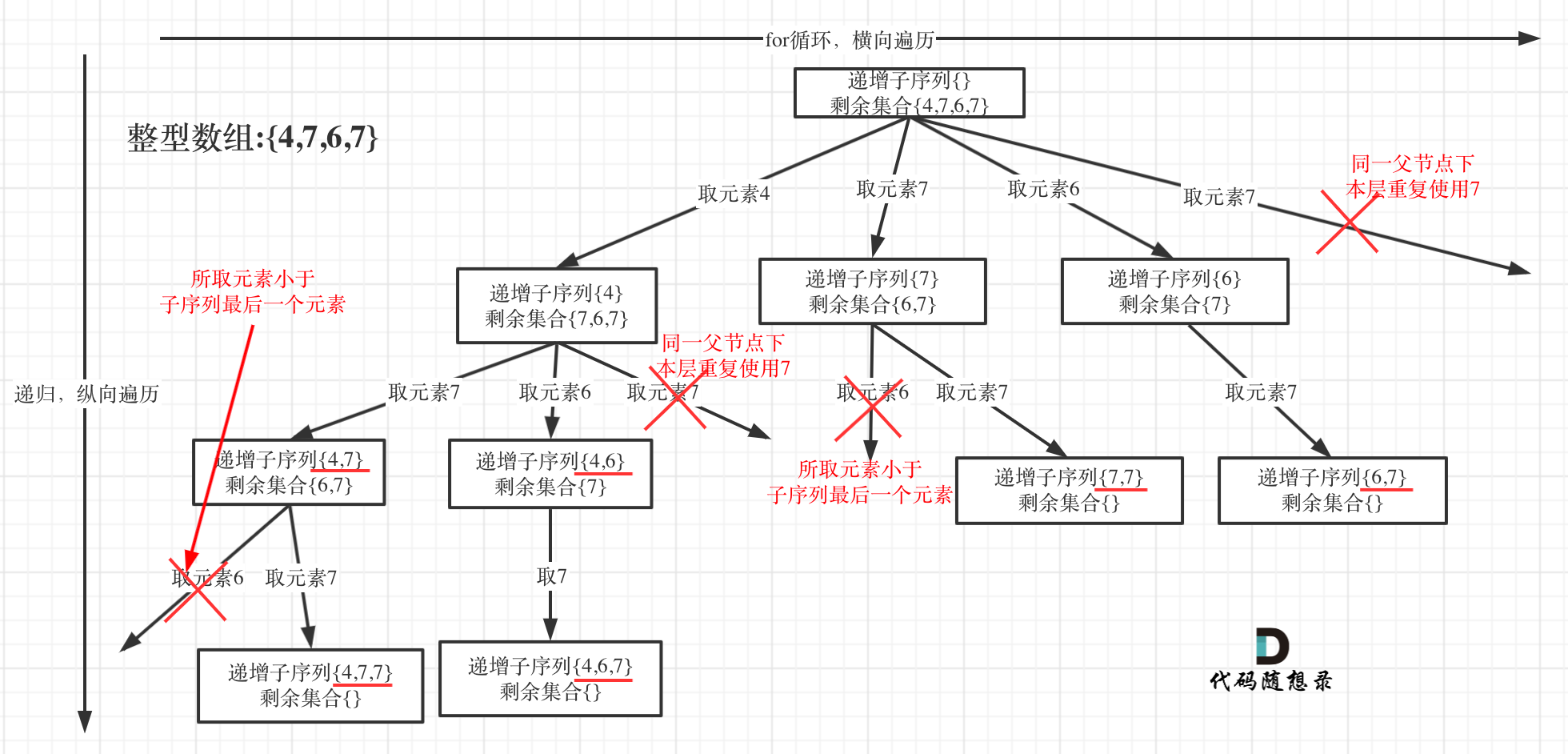
在图中可以看出,同一父节点下的同层上使用过的元素就不能再使用了
代码:
class Solution:
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
result = []
path = []
self.backtracking(nums, 0, path, result)
return result
def backtracking(self, nums, startIndex, path, result):
if len(path) > 1:
result.append(path[:]) # 注意要使用切片将当前路径的副本加入结果集
# 注意这里不要加return,要取树上的节点
uset = set() # 使用集合对本层元素进行去重
for i in range(startIndex, len(nums)):
if (path and nums[i] < path[-1]) or nums[i] in uset:
continue
uset.add(nums[i]) # 记录这个元素在本层用过了,本层后面不能再用了
path.append(nums[i])
self.backtracking(nums, i + 1, path, result)
path.pop()- 时间复杂度: O(n * 2^n)
- 空间复杂度: O(n)
46. 全排列
思路:
此时我们已经学习了77.组合问题 (opens new window)、 131.分割回文串 (opens new window)和78.子集问题 (opens new window),接下来看一看排列问题。
我以[1,2,3]为例,抽象成树形结构如下:
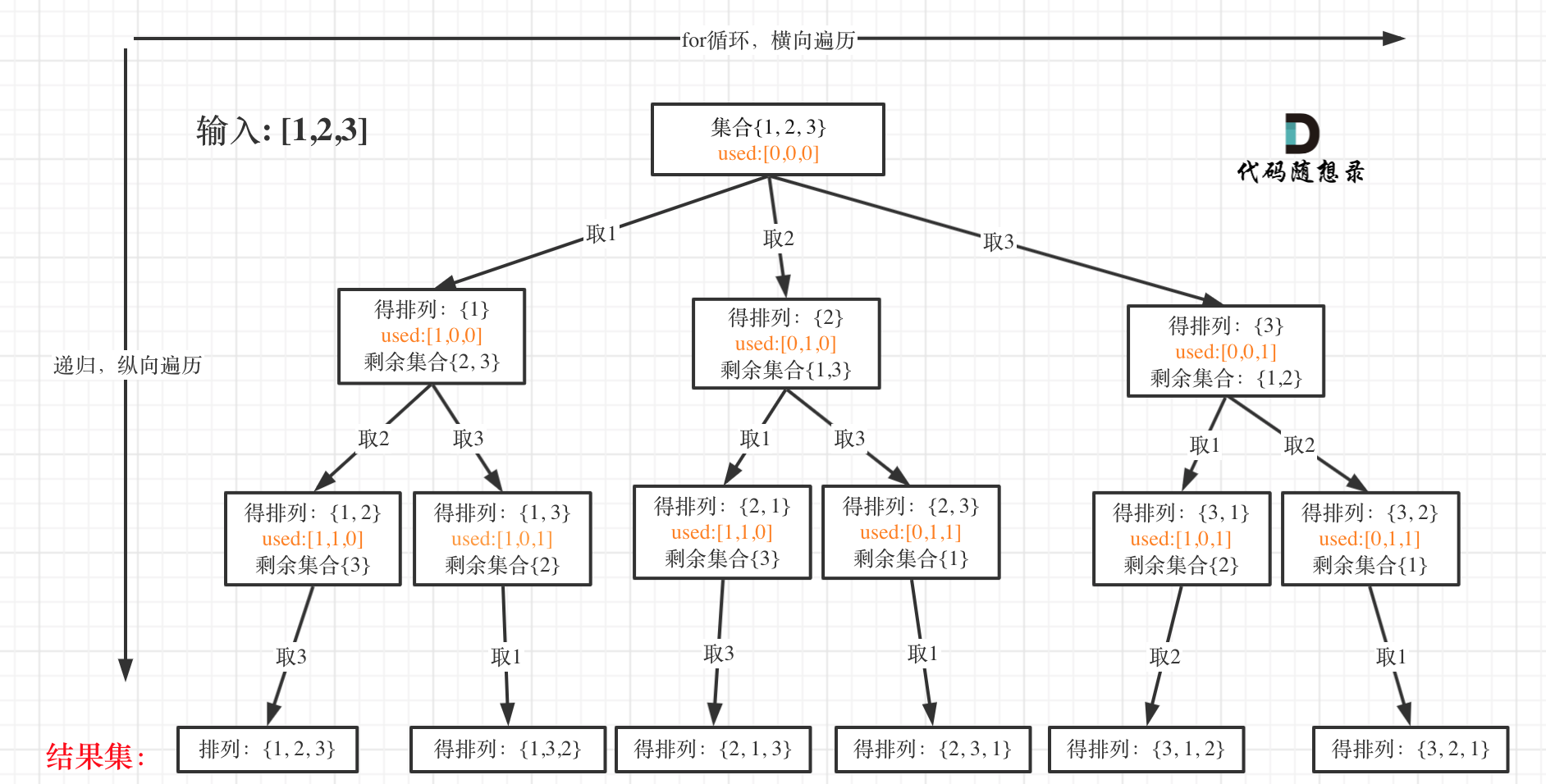
这里和77.组合问题 (opens new window)、131.切割问题 (opens new window)和78.子集问题 (opens new window)最大的不同就是for循环里不用startIndex了。
因为排列问题,每次都要从头开始搜索,例如元素1在[1,2]中已经使用过了,但是在[2,1]中还要再使用一次1。
而used数组,其实就是记录此时path里都放了哪些元素,一个排列里一个元素只能使用一次。
代码:
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
result = []
path = []
self.backtracking(nums, path, [False] * len(nums), result)
return result
def backtracking(self, nums, path, used, result):
if len(path) == len(nums):
result.append(path[:])
return
for i in range(len(nums)):
if used[i]:
continue
used[i] = True
path.append(nums[i])
self.backtracking(nums, path, used, result)
path.pop()
used[i] = False- 时间复杂度: O(n!)
- 空间复杂度: O(n)
47. 全排列 II
思路:
这道题目和46.全排列 (opens new window)的区别在与给定一个可包含重复数字的序列,要返回所有不重复的全排列。
这里又涉及到去重了。
还要强调的是去重一定要对元素进行排序,这样我们才方便通过相邻的节点来判断是否重复使用了。
我以示例中的 [1,1,2]为例 (为了方便举例,已经排序)抽象为一棵树,去重过程如图:
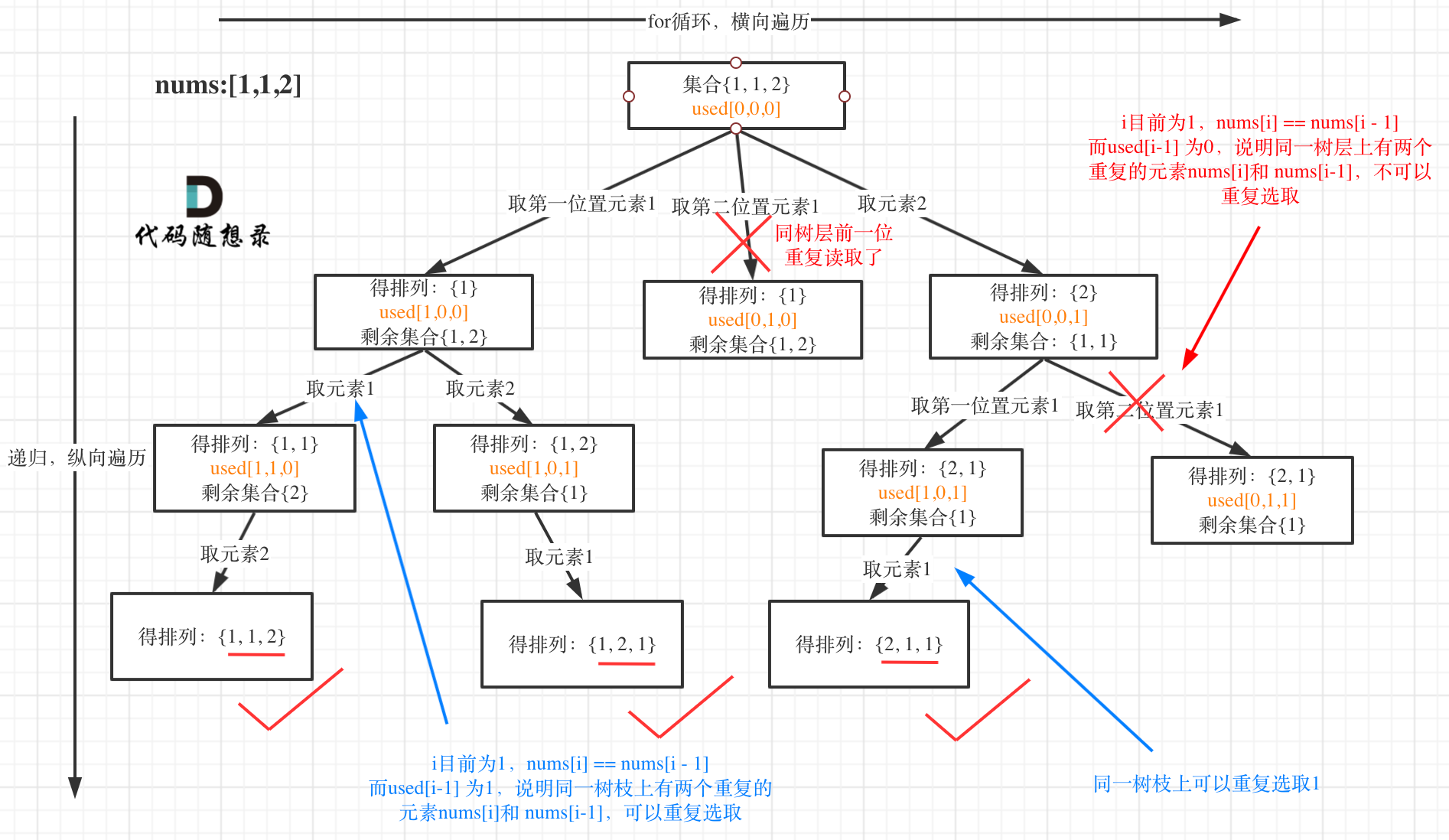
代码:
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
nums.sort() # 排序
result = []
path = []
self.backtracking(nums, path, [False] * len(nums), result)
return result
def backtracking(self, nums, path, used, result):
if len(path) == len(nums):
result.append(path[:])
return
for i in range(len(nums)):
if i > 0 and nums[i] == nums[i - 1] and used[i-1]==False:
continue
if used[i]==True:
continue
used[i] = True
path.append(nums[i])
self.backtracking(nums, path, used, result)
path.pop()
used[i] = False- 时间复杂度: O(n! * n)
- 空间复杂度: O(n)