---

在《强化学习（三）基于动态规划 Dynamic Programming 的求解方法》的文末中提到，利用动态规划迭代地求解强化学预测和控制问题，当待更新估计价值的状态的后续状态过多时，每次迭代所消耗的计算资源将指数级增长直至动态规划不再适用。而且，运用动态规划还有一个重要前提是，环境的状态转移模型 $P$ （状态转移概率）和奖励函数都是确定已知的，即解决的是模型依赖（Model-Based RL）的强化学习问题，对于模型无关（Model-Free RL）的问题则不适用。而本文将介绍的蒙特卡罗方法（Monte-Calo，MC）则是一种既能应对大规模问题，又适用于模型无关的强化学习问题的方法。

1. 免模型学习的强化学习问题

前文提到，强化学习当中的两个基本问题为预测和控制，在运用动态规划求解的两类问题分别是：

1. 预测问题（策略评估）。给定强化学习的状态集 $S$，动作集 $A$，模型状态转化概率矩阵 $P$，采取动作的即时奖励 $R$，奖励衰减因子 $\gamma$，以及动作策略 $\pi$，在这些条件下，求解策略 $\pi$ 的状态价值函数 $v(\pi )$；
2. 控制问题（策略迭代）。给定强化学习的状态集 $S$，动作集 $A$，模型状态转化概率矩阵 $P$，采取动作的即时奖励 $R$，奖励衰减因子 $\gamma$，求解最优的状态价值函数 $v_{\ast }$ 和最优策略 ${\pi }_{\ast }$。

如上所述，运用动态规划求解的这类问题的环境状态转移概率矩阵 $P$ 是已知的，一般称为有模型学习或基于模型的学习问题（Model-Based）。然而现实中的很多强化学习场景，是没有先验知识或者是环境模型的先验信息的，例如无法事先得到模型的状态转化概率矩阵 $P$，这类问题就称为免模型学习或不基于模型的学习问题（Model-Free），此时就需要通过与环境的直接交互来学习策略和值函数，而不用对环境的模型进行假设，因此免模型的强化学习方法天然地适应各种类型的问题，但也面临着需要更多的样本数据进行学习和某些情况下难以收敛于最优解等问题。

免模型的强化学习问题的两个基本问题可以重定义为：

1. 预测问题（策略评估）。给定强化学习的状态集 $S$，动作集 $A$，采取动作的即时奖励 $R$，奖励衰减因子 $\gamma$，以及给定策略 $\pi$，在这些条件下（状态转移概率 $P$ 未知），求解策略 $\pi$ 的状态价值函数 $v(\pi )$；
2. 控制问题（策略迭代）。给定强化学习的状态集 $S$，动作集 $A$，采取动作的即时奖励 $R$，奖励衰减因子 $\gamma$，探索率 $ϵ$，求解最优的状态价值函数 $v_{\ast }$ 和最优策略 ${\pi }_{\ast }$。

2. 利用蒙特卡洛法求解最优价值函数

蒙特卡罗方法（Monte-Calo，MC）是一种基于随机抽样和统计分析的数值计算方法，可以用于求解无模型的强化学习问题的策略评估和迭代。其基本思想就是，通过大量的随机抽样来近似未知信息，最终用得到的近似信息求解复杂的问题，因此该方法具有极高的适应性。

在强化学习当中，通过蒙特卡罗方法采样若干完整的状态序列（episode）来估计状态的价值，这里的完整序列指的是到达终点的状态序列，例如在《【项目案例】利用强化学习训练“井字棋”下棋策略的详细介绍》指的是对弈结束时，所存储的从开始到结束的状态序列。

2.1 策略评估（预测）

在给定一个策略的前提下，对该策略下的各个状态价值进行评估。基于该策略 $\pi$ 进行模拟并采集（确定的）完整的状态序列，可以通过下式，从结束状态的价值逆推得到各个状态的价值：

$$v_{\pi }(s)=R_t^a+\gamma v_{\pi }(s^{\prime })=G_t$$

由于 $v_{\pi }(s)={\mathbb{E}}_{\pi }(G_t|S_t=s)$ 可得，每个状态的价值函数等于所有样本中，该状态所获价值的期望（平均）。因此，对于蒙特卡罗方法而言，如果要求某一个状态的状态价值，则需要求出所有的完整序列样本中出现该状态时的收获价值，再取平均即为该状态的近似价值，公式如下：

$$v_{\pi }(s)\approx \text{mean}(G_t),\text{if }{S}_t=s$$

总体的思路即是用模拟产生的序列的状态价值的期望来估计实际的状态价值。但是实际的计算过程中，可能会有以下的一些问题：

（1）在一个状态序列中，可能重复出现同样的状态，该状态的 $G_t$ 值如何计算？

针对这个问题有两种解决办法：

1. 将状态序列中首次出现该状态时的收获价值设为 $G_t$；
2. 针对序列中每次出现的该状态 $s$，都计算对应的收获值并纳入平均值计算当中，即该状态序列下会有 $G_{t1},G_{t2}...$ 多个 S t = s , ∀ t ∈ { t 1 , t 2... } S_t=s,\forall t\in \{t1,t2...\} St​=s,∀t∈{t1,t2...}

（2）在模拟采样过程中，我们需要对所有状态的每次出现的 $G_t$ 结果值进行记录后再取平均，对于复杂问题，迭代到后期需要存储的数据量非常多，如何在迭代地更新状态价值以节约存储空间？

可以在每次迭代的时候都更新计算得到最新的状态价值，根据如下式子，每得到一个新的状态序列的状态价值 $x_k$，还需要记录总共的纳入均值计算的状态价值个数 $k$，即可根据前一个均值 ${\mu }_{k-1}$ 计算出纳入新价值后的均值 ${\mu }_k$，具体公式如下：

$${\mu }_k=\frac{1}{k}\sum _{j=1}^k{x}_j=\frac{1}{k}\left(x_k+\sum _{j=1}^{k-1}{x}_j\right)=\frac{1}{k}\left(x_k+(k-1){\mu }_{k-1}\right)={\mu }_{k-1}+\frac{1}{k}(x_k-{\mu }_{k-1})$$

根据上面的公式可知，根据采样数据，状态每纳入一个新的用以求平均的值 $G_t$ 时，总数 $N(s)=N(s)+1$，新的状态期望价值 $v(s)$ 更新为：

$$v(s)=v(s)+\frac{1}{N(s)}\left(G_t-v(s)\right)$$

该步骤的计算的渐进复杂度不变，空间复杂度却降至 $O(1)$，显然地，当输入的完整状态序列越多，则 $v(s)$ 的更新量越小，也越接近实际的状态价值。有时对于海量数据的分布迭代计算，可能会出现并行迭代的情况，因此无法准确估计当前一共纳入计算平均值的状态价值有多少个，因此常常会用一个学习率 $\alpha$ 替代 $1/N$，上式更新为 $v(s)=v(s)+\alpha \left(G_t-v(s)\right)$。

2.2 策略迭代（控制）

在前文中，动态规划进行值迭代的思路是，先对当前策略进行评估，计算出状态价值函数，然后基于一定方法（贪婪法），在每个状态处选择后续状态价值最大的动作，更新当前策略，迭代多次最后得到最优价值函数。

蒙特卡洛与动态规划除了在策略评估方法上的差异，在策略迭代上也有所不同。首先是优化对象，动态规划既可以优化状态价值函数，也可以优化动作价值函数，而蒙特卡洛由于每次模拟只得到具体的动作及状态序列，并不知道每一步的可选状态空间，因此一般优化的是动作价值函数 $q_{\ast }$，其次不同的是策略更新的方法，动态规划一般用贪婪法更新策略，这是在环境模型以及动作奖励都已知前提下，而蒙特卡罗法通常采用的是 $ϵ-$贪婪法，探索率 $ϵ$ 表示当前阶段随机选择动作的概率，而以 $1-ϵ$ 的概率按贪婪的方法选择动作，此时策略选择到最优的动作 $a^{\ast }$ 的概率为：$ϵ/m+1-ϵ$。

在相关示例《【项目案例】利用强化学习训练“井字棋”下棋策略的详细介绍》中，模拟对弈阶段，设置一个探索率，使得在模拟过程中可以不断地生成新的状态序列，以避免错过更优价值动作序列。

同时在该案例中，棋手的价值函数会在每次模拟对弈后进行更新，这种智能体从历史数据中学习，并根据历史数据更新策略的方式称为离线学习（off-policy），而在线学习（on-policy）则是在与环境实时交互的过程中，不断地根据交互结果进行学习更新。

这里介绍在线蒙特卡罗方法求解强化学习可知问题的流程，输入内容为：状态集 $S$，动作集 $A$，采取动作的即时奖励 $R$，奖励衰减因子 $\gamma$，探索率 $ϵ$；输出内容为：最优的动作价值函数 $q_{\ast }$ 和最优策略 ${\pi }_{\ast }$。具体流程如下：

1. 初始化所有的动作价值 $Q(s,a)=0$，状态次数 $N(s,a)=0$，采样次数 $k=0$，初始策略为随机策略 $\pi$；
2. 在第 $k=k+1$ 代，基于策略 $\pi$ 进行第 $k$ 次蒙特卡罗采样，得到的完整状态序列：$S_1,A_1,R_1,S_2,A_2,...S_t,A_t,R_t,....S_{T-1},A_{T-1},R_{T-1},S_T$
3. 对于状态序列里出现的每一状态行为对 $(S_t,A_t)$，按照前面策略评估的方式，先计算出动作价值 $Q(S_t,A_t)$，再更新迭代状态行为对的价值：
   $$\begin{gathered} N(S_t,A_t)=N(S_t,A_t)+1 \\ Q(S_t,A_t)=Q(S_t,A_t)+\frac{1}{N(S_t,A_t)}\left(G_t-Q(S_t,A_t)\right) \end{gathered}$$
4. 取 $ϵ=1/k$，基于新计算出的动作价值，用 $ϵ-$ 贪婪策略对当前策略进行调整；
5. 循环迭代 $2\sim 4$ 步，直至所有的状态动作对 $Q(s,a)$ 都收敛（更新量非常小），则所有的 $Q(s,a)$ 对应的就是最优动作价值函数 $q$，对应的的策略 $\pi (a|s)$ 即为最优策略 ${\pi }_{\ast }$。

这里我们为了方便比较，还是举 UCL 强化学习讲义中的例子（也可以在前面的文章中查看），如下图，这是已知环境转移概率模型 $P$ 的前提下，用动态规划求解得到的各个状态动作对的最优动作函数 $q$。

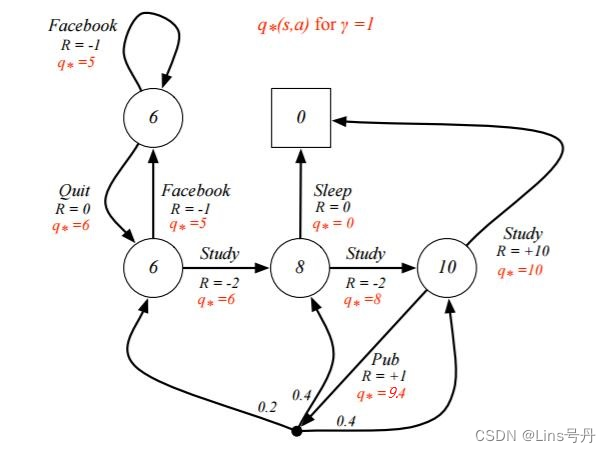
现在我们用上述的蒙特卡罗方法来计算最优动作价值函数，在每次迭代过程中，根据一定的探索率 $ϵ=1/k$ 生成一个完整状态序列，接着计算状态动作对的价值 $G$，并结合出现次数更新状态 $s$ 下动作 $a$ 的估计价值，具体代码如下：

import random

s_a = {"s1": {"facebook": ["s1"], "quit": ["s2"]},
       "s2": {"facebook": ["s1"], "study": ["s3"]},
       "s3": {"sleep": ["s0"], "study": ["s4"]},
       "s4": {"study": ["s0"], "pub": ["s2", "s3", "s4"]}}
q = {(s,a):0 for s in s_a for a in s_a[s]}
r = {("s1", "facebook"): -1, ("s1", "quit"): 0,
     ("s2", "facebook"): -1, ("s2", "study"): -2,
     ("s3", "sleep"): 0, ("s3", "study"): -2,
     ("s4", "study"): 10, ("s4", "pub"): 1}
     
num_s_a = {(s,a):0 for s in s_a for a in s_a[s]}
k = 0

for k in range(1, 2000):
    s = "s1"
    seq = []
    while s != "s0":
        if random.random() < 1/k:
            a = random.choice(list(s_a[s].keys()))
        else:
            a = max(s_a[s], key=lambda x: q[s,x])
        seq.append((s,a))
        s = random.choice(s_a[s][a])
    # print(seq)
    G = 0
    for pair in seq[::-1]:
        num_s_a[pair] += 1
        G += r[pair]
        q[pair] = q[pair] + (1/num_s_a[pair])*(G-q[pair])
            
print(q)

经过 $10000$ 次迭代，求得的动作价值函数，与上图的最优价值函数绝对离差和为 $2.4$，结果已经非常地接近。

{('s1', 'facebook'): 5.0, ('s1', 'quit'): 5.994002998500746, ('s2', 'facebook'): 5.0, ('s2', 'study'): 5.994600539946007, ('s3', 'sleep'): 0.0, ('s3', 'study'): 7.999399699849905, ('s4', 'study'): 10.0, ('s4', 'pub'): 7.0}

在实验中发现，带有探索率的蒙特卡罗方法的求解结果具有一定的波动性，且在迭代次数较少时，这种波动性越大，而随着迭代采样的次数增大，求解结果的波动范围逐渐缩小，且更加靠近最优的动作状态函数。

注意这里的探索率 $ϵ$，随着迭代的进行会逐渐减小，这是为了保证算法的收敛性。此外，过大的探索率会导致花费过多时间在探索上而忽视对已知优秀策略的学习；过小的探索率则可能导致策略早熟陷入局部最优，因此具体的探索率大小需要在实际中通过调参进行权衡。

这里不论怎么求，结果与实际最优价值函数总是有一定的误差，这是由于原题目在 $s_4$ 处采取了动作 pub 之后，状态转移至三个后续状态的概率不是均等的，而在代码中我直接用的是随机转移，用来模拟所谓的对环境先验知识未知的情况，但这种确定的分布概率也可以考虑进代码当中，模拟实际环境的状态反馈，这个留给大家试一下。