Python数据结构【二】查找

news2024/10/6 16:23:46

前言

可私聊进一千多人Python全栈交流群（手把手教学，问题解答）
进群可领取Python全栈教程视频 + 多得数不过来的计算机书籍：基础、Web、爬虫、数据分析、可视化、机器学习、深度学习、人工智能、算法、面试题等。

🚀🚀加入我一起学习进步，一个人可以走的很快，一群人才能走的更远！

一、查找是什么

查找，顾名思义，就是找某个东西。

不过一般都是在某个数据结构里面查找，有在数组(Python是列表)查找的，有在链表查找的，有在字典查找的。

较为官方的描述

在一些数据元素中，通过一定的方法找出给定的数据元素。

在编程中，查找总是与循环挂钩的，而又分为，线性查找，二分查找等查找方法。

二、线性查找

线性查找就比较简单了，就是在列表中顺序查找某个元素。

上代码！

def find_num(li,num):
    """
    li: 列表
    num: 要找的数
    """
    for i in range(len(li)):
        if li[i]==nums:
            return i
    return None

这就是一个简简单单的线性查找，找出列表中是否存在某个元素，如果存在，就返回下标，不存在就返回None

当然，这只是最基础的，说的稍微进阶的，这就不得不拿出力扣的第一题了，我第一次做力扣的时候就有点头疼

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target  的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

两数之和实例

实例1

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

实例2

输入：nums = [3,2,4], target = 6
输出：[1,2]

实例3

输入：nums = [3,3], target = 6
输出：[0,1]

两数之和解析(线性查找版)

顾名思义，挨个找，然后判断，然后返回下标，然后由于我们需要判断两个元素的和是否符合题目，所以我们就需要嵌套循环来实现在同一个列表中查找两个元素的和。

代码实现

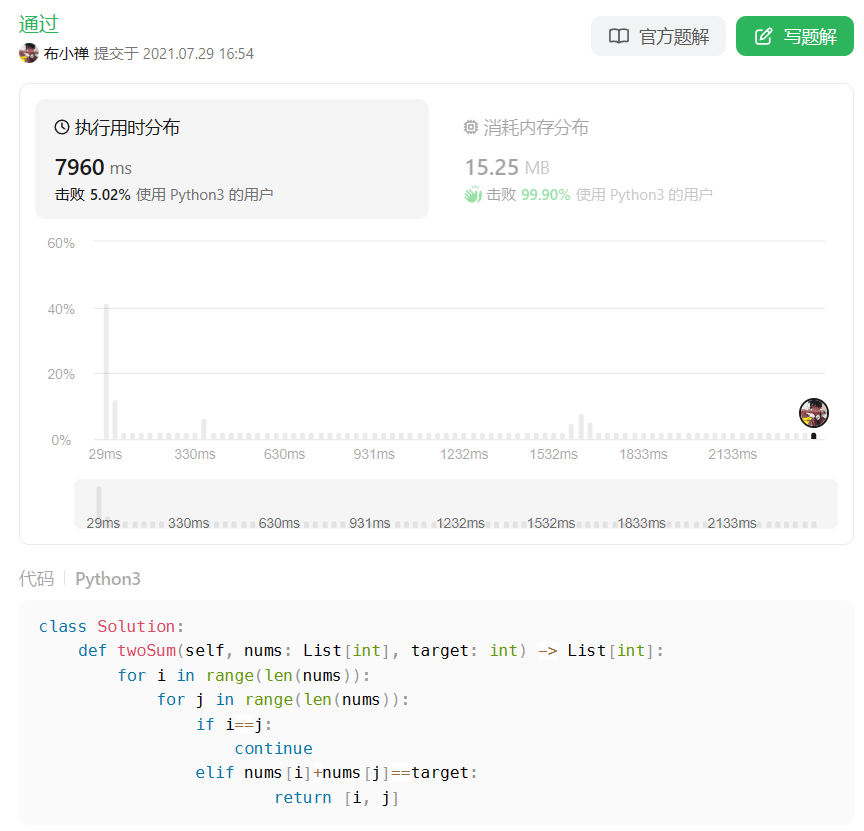
class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        for i in range(len(nums)):
            for j in range(len(nums)):
                if i==j:
                    continue
                elif nums[i]+nums[j]==target:
                        return [i, j]

通过截图：

在这里插入图片描述

三、二分查找

二分查找就是分出两个指针，分别在头部尾部，然后头部指针加，尾部指针减来比对两数之和(当然使用二分的前条件的列表是有序的)

如果首尾指针对应的元素和比题目给定的两数之和大，就说明当前的和较大，将查找范围减半，将尾部指针跳转到中间

如果小，就说明两个元素之和较小，就将范围减小一半，将首部指针跳转到中间。

然后直到查找完毕。

还是上个图吧

在这里插入图片描述

练习

题目：

给定一个列表[1, 3, 6, 8, 10, 13]，找出两数之和为9的两个元素，并返回它们的下标

代码：

def mid_find(li, num):
    left = 0                        # 首部指针
    right = len(li) - 1             # 尾部指针
    for i in range(len(li)):        # 循环
        mid = (left + right + 1) // 2   # 指针跳转位置
        if li[left] + li[right] == num and left != right:
            # 符合的直接返回
            return [left, right]
        elif li[left] + li[right] > num:
            right = mid
        else:
            left = mid
li = [1, 3, 6, 8, 10, 13]
print(mid_find(li, 9))

运行结果：

在这里插入图片描述

二分查找库bisect_left函数

使用方法：

j = bisect.bisect_right(li, num, right, n)

li：要查找的数组

num：要查找的数

right：上界

n：长度

返回的是大于等于要查找数的第一个下标

所以我们的代码就可以写成：

def mid_find(li, num):
    left = 0                        # 首部指针
    right = len(li) - 1             # 尾部指针
    for i in range(len(li)):        # 循环
        t = num-li[i]
        j = bisect_left(li,t, i+1, len(li))
        if j < len(li) and li[j] == t:
            return [i,j]
li = [1, 3, 6, 8, 10, 13]
print(mid_find(li, 9))

运行结果：

在这里插入图片描述

两数之和解析(二分版)

首先肯定是需要先排序的，那么排完序不就好做了吗？

不，这个题的难点在于需要返回的是原列表的下标，所以我们在使用排序的时候，还得保证得到答案后我们返回的下标是原来没有排序的下标

所以我们就需要将原列表和下标进行一个绑定，使用zip函数

代码：

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        n = len(nums)                   # 列表长度
        nums = sorted(zip(nums,range(n)))        # 排序
        for i in range(n):
            t = target-nums[i][0]
            j = bisect_left(nums, (t, ), i+1, n)
            if j < n and nums[j][0] ==t:
                return [nums[i][1], nums[j][1]]
        return []