---

1.背景

2023年，M Azizi等人受到物理理论粒子稳定性与衰变性启发，提出了能量谷优化算法（Energy Valley Optimizer, DVO）。

2.算法原理

2.1算法思想

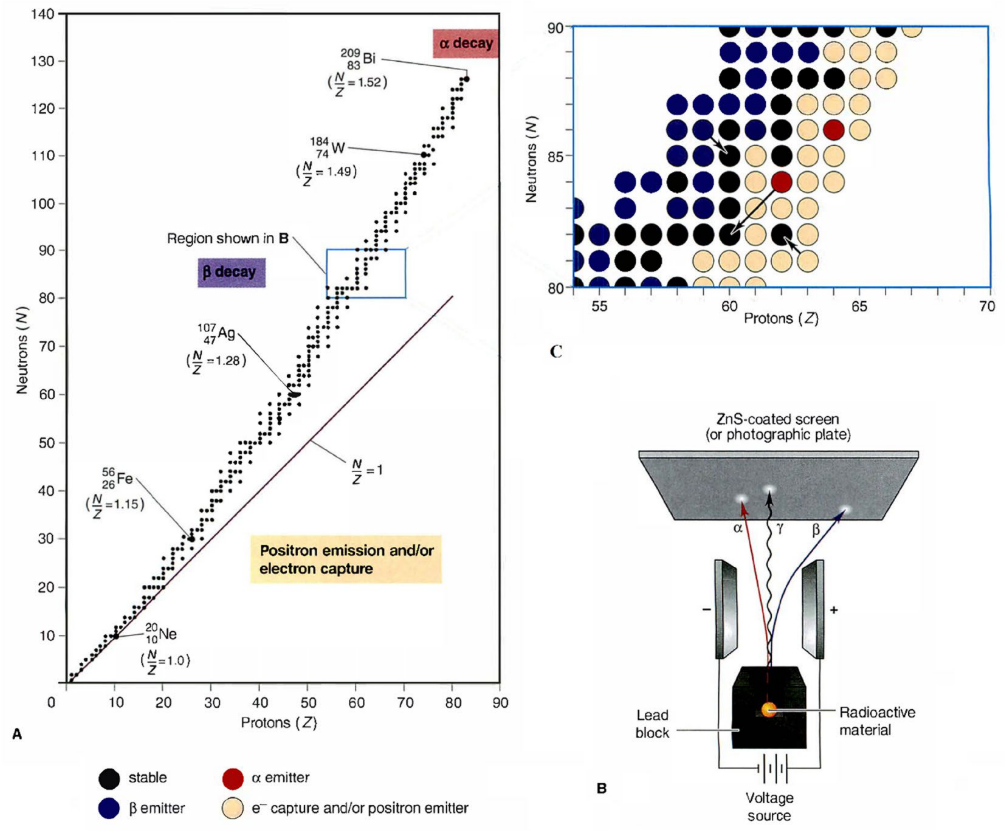
EVO基于粒子物理反应的优化过程。在这个过程中，稳定性较差的粒子会通过衰变释放能量，并趋向于向能量谷或稳定带移动，以提高其稳定性水平。这种物理过程启发了元启发式算法的发展，其中候选解倾向于逐步改进以达到更稳定的状态。

2.2算法过程

考虑富中子粒子和贫中子粒子之间的差异，对每个粒子进行目标函数评价，并确定为粒子的中子富集水平(NEL)：
$$\mathrm{EB}=\frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\mathrm{NE}{\mathrm{L}}_{\mathrm{i}}}{\mathrm{n}},\mathrm{i}=1,2,\dots ,\mathrm{n}\text{\hspace{1em}(1)}$$
式中，NELi为第i个粒子的中子富集能级，EB为宇宙中粒子的富集界。

确定粒子的稳定水平:
$$\mathrm{S}{\mathrm{L}}_{\mathrm{i}}=\frac{\mathrm{NE}{\mathrm{L}}_{\mathrm{i}}-\mathrm{BS}}{\mathrm{WS}-\mathrm{BS}},\mathrm{i}=1,2,\dots ,\mathrm{n}\text{\hspace{1em}(2)}$$
其中，SLi为第i个粒子的稳定水平，BS和WS为宇宙内稳定水平最佳和最差的粒子。

如果粒子的中子富集水平高于富集界(NELi > EB)，则假设该粒子具有较大的N/Z比，因此采用α、β或γ衰变过程。在[0,1]范围内生成一个随机数，它模拟了宇宙中的稳定界(Stability Bound, SB)。如果粒子的稳定水平高于稳定界(SLi > SB)，则认为发生α和γ衰变。

发射的射线是候选溶液中的决策变量，将其去除并替换为具有最佳稳定水平(XBS)的粒子或候选溶液中的射线：
$${\mathrm{X}}_{\mathrm{i}}^{New1}={\mathrm{X}}_{\mathrm{i}}\left({\mathrm{X}}_{\mathrm{BS}}\right({\mathrm{x}}_{\mathrm{i}}^{\mathrm{j}}\left)\right),\{\begin{array}{c}i=1,2,\dots ,n.\\ j=AlphaIndexII.\end{array}\text{\hspace{1em}(3)}$$
其中，Xi为第i个粒子(解候选)的当前位置向量，XBS为稳定性等级最好的粒子的位置向量。

在伽马衰变中，发射γ射线以提高受激粒子的稳定性水平，位置更新为：
$${\mathrm{D}}_{\mathrm{i}}^{\mathrm{k}}=\sqrt{({\mathrm{x}}_2-{\mathrm{x}}_1{)}^2+{\left({\mathrm{y}}_2-{\mathrm{y}}_1\right)}^2},\{\begin{array}{c}i=1,2,\dots ,n.\\ k=1,2,\dots ,n-1.\end{array}\text{\hspace{1em}(4)}$$
第二个候选解决方案位置更新为：
$${\mathrm{X}}_{\mathrm{i}}^{\mathrm{N}ew2}={\mathrm{X}}_{\mathrm{i}}\left({\mathrm{X}}_{\mathrm{N}g}\right({\mathrm{x}}_{\mathrm{i}}^{\mathrm{j}}\left)\right),\{\begin{array}{c}i=1,2,\dots ,n.\\ j=\text{Gamma Index II}.\end{array}\text{\hspace{1em}(5)}$$
其中，XNg为第i个粒子周围邻近粒子的位置向量。

如果粒子的稳定水平低于稳定界(SLi≤SB)，则认为发生了β衰变。β射线从粒子中释放出来，以提高粒子的稳定水平，因此由于这些粒子的不稳定水平较高，应该在搜索空间中进行大的跳跃：
$$\begin{gathered} {\mathrm{X}}_{\mathrm{CP}}=\frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{X}}_{\mathrm{i}}}{\mathrm{n}},\mathrm{i}=1,2,\dots ,n. \\ {\mathrm{X}}_{\mathrm{i}}^{New1}={\mathrm{X}}_{\mathrm{i}}+\frac{({\mathrm{r}}_1\times {\mathrm{X}}_{\mathrm{BS}}-{\mathrm{r}}_2\times {\mathrm{X}}_{\mathrm{CP}})}{\mathrm{S}{\mathrm{L}}_{\mathrm{i}}},\mathrm{i}=1,2,\dots ,n.\text{\hspace{1em}(6)} \end{gathered}$$
其中，XBS是稳定水平最好的粒子的位置向量，XCP是粒子中心的位置向量。
为了提高算法的开发和探索水平，对采用β衰变的粒子进行另一个位置更新过程，在粒子的稳定水平不影响运动过程的情况下，对具有最佳稳定水平(XBS)的粒子或候选粒子和邻近的粒子或候选粒子(XNg)进行控制：
$${\mathrm{X}}_{\mathrm{i}}^{New2}={\mathrm{X}}_{\mathrm{i}}+\left(\begin{array}{c}{r}_3\times X_{BS}-r_4\times X_{Ng}\end{array}\right),\mathrm{i}=1,2,\dots ,n.\text{\hspace{1em}(7)}$$
其中，XBS是稳定性水平最好的粒子的位置向量，XNg是第i个粒子周围邻近粒子的位置向量。
如果粒子的中子富集水平低于富集界(NELi≤EB)，则认为该粒子的N/Z比较小，因此粒子倾向于通过电子捕获或正电子发射向稳定带移动：
$${\mathrm{X}}_{\mathrm{i}}^{\mathrm{New}}={\mathrm{X}}_{\mathrm{i}}+\mathrm{r},\mathrm{i}=1,2,\dots ,n.\text{\hspace{1em}(8)}$$

伪代码

3.结果展示

4.参考文献

[1] Azizi M, Aickelin U, A. Khorshidi H, et al. Energy valley optimizer: a novel metaheuristic algorithm for global and engineering optimization[J]. Scientific Reports, 2023, 13(1): 226.