傅里叶变换到底是什么
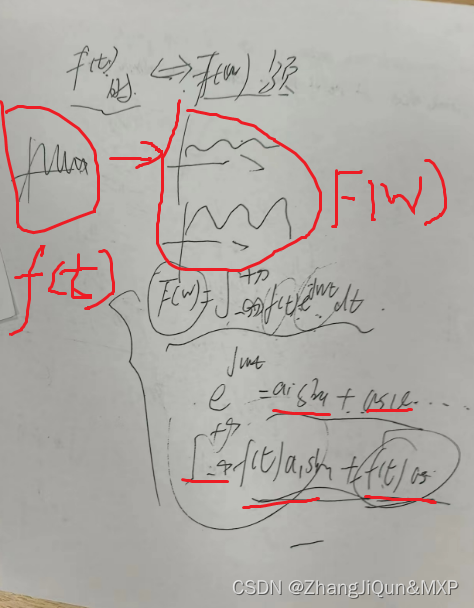
有一个f(t)经傅里叶变换公式转化成F(w);
F(w)包括 欧拉公式转化成无限包括sin cos的函数相加。sin cos前面的参数a不为0说明这个周期函数分量存在,是某一种有效成分。
复试实质是拓展了坐标空间到三维
复数是数学中的一个基础概念,用于表示包含实数和虚数部分的数。它们通常以a+bi的形式表示,其中a为实部,b为虚部,i为虚数单位。由于i的定义是i^2=-1,而任何实数的平方不可能为-1,因此i不是实数,而是实数以外的新的数。
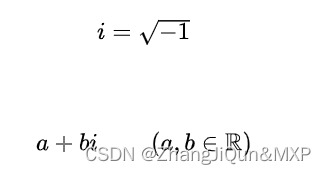
傅里叶变换例题


有一个f(t)经傅里叶变换公式转化成F(w);
F(w)包括 欧拉公式转化成无限包括sin cos的函数相加。sin cos前面的参数a不为0说明这个周期函数分量存在,是某一种有效成分。
复数是数学中的一个基础概念,用于表示包含实数和虚数部分的数。它们通常以a+bi的形式表示,其中a为实部,b为虚部,i为虚数单位。由于i的定义是i^2=-1,而任何实数的平方不可能为-1,因此i不是实数,而是实数以外的新的数。
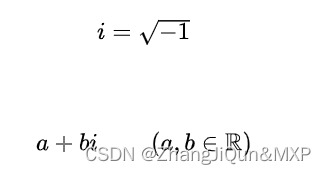

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1600203.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!