一、基本概念

 

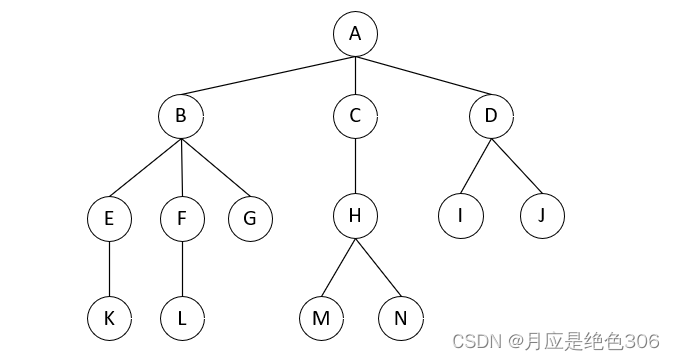
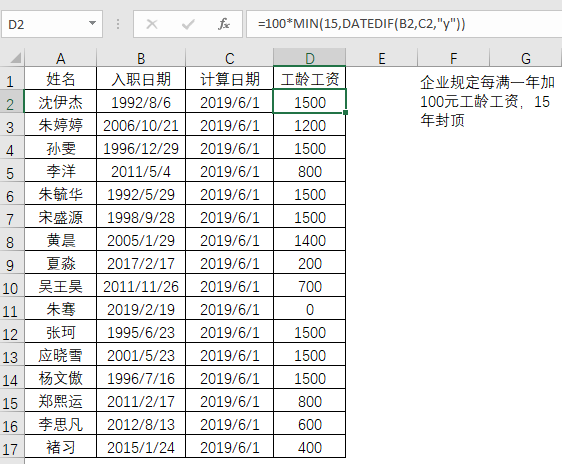
1.最左孩子结点：一个结点的孩子结点中位于最左边的孩子结点。例如，A——B，B——E；
2.树的高度：树的最高层数；
3.路径长度：树中的任意两个顶点之间都存在唯一的一条路径。一条路径所经过的边的数量称为路径长度；
4.树的直径：树中的最长路径，图中树的直径为6；
5.兄弟节点：拥有共同父节点（B、C、D），E的右兄弟节点为F，F的左兄弟节点为E；
6.堂兄弟结点：父结点的父结点（祖父结点，对应就是子孙结点）相同（K和L）；
7.叔叔结点：C为E的叔叔结点
8.度：一个结点子树的数量（A-3，E-1）
 

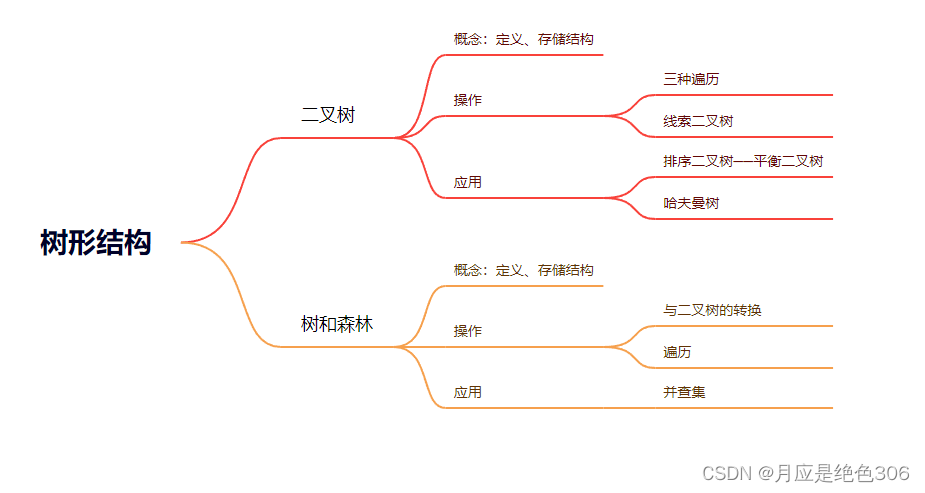
二、二叉树

二叉树是最常使用的树形结构，其存储结构及其相关操作都较为简单，堆、AVL树、红黑树等都属于二叉树。

定义：

二叉树是节点的度不超过2的树形结构。

性质：
1.二叉树的第i层上最多有个结点(i>=1)；
2.在一棵高度为h的二叉树中，最多有个结点，最少有h个结点；
3.如果一棵二叉树有n个结点，则该二叉树有n-1条边；
4.在一棵二叉树中，如果度为0的结点（叶结点）数为n0，度为2的结点数为n2，则n0=n2+1。

创建如下二叉树： （以下代码皆基于这张图）

 
        前面创建二叉树的方法是多次调用 create_lrpTree函数，操作比较烦琐，这里介绍如何利用扩展二叉树的先根序列创建二叉树。扩展二叉树是指将二叉树的空指针域指向一个特殊的结点，并将这特殊结点赋予一个特殊的值(如#）。扩展二叉树中称原结点为内结点，而添加的结点为外结点，显然，在扩展二叉树中，外结点的数量比内结点的数量多1，且每个内结点都有两个孩子。

        以上图所示的扩展二叉树的先根序列为：ABD##EG###CF#H###。

#include<iostream>
#include<stack>
using namespace std;

/*
	左右链指针表示法，这是左右链指针表示二叉树结点的常见表示方法
	这种方法只能自顶向下遍历二叉树，通常用二叉树的根结点表示二叉树。
	由于二叉树的一个结点的左右子树结构与原二叉树具有相似的结构，
	因此对二叉树的操作通常采用递归的方法。
*/
// 孩子表示法
typedef char datatype;
typedef struct lrpNode {
	datatype data;   //数据域
	lrpNode* lc, * rc; //左右链域
	lrpNode():lc(NULL), rc(NULL) {
		data = 0;
	}
}*lrpTree;

// 孩子双亲表示法
// 在结点中添加parent之后不仅可以对二叉树进行自顶向下的操作，而且可以进行自底向上的操作
//typedef struct lrpNode {
//	datatype data;   //数据域
//	lrpNode* lc, * rc,*parent; //左右链域
//	lrpNode() :lc(NULL), rc(NULL),parent(NULL) {
//		data = 0;
//	}
//}*lrpTree;

// 创建一棵二叉树，其根节点的数据值为data，左右孩子分别为lc，rc
// 用该函数创建一棵二叉树，应该从二叉树的最底层开始，自下而上依次创建
lrpTree create_lrpTree(datatype data, lrpTree lc, lrpTree rc) {
	lrpTree tmp = new lrpNode; //为根结点动态分配存储空间
	tmp->data = data;
	tmp->lc = lc;
	tmp->rc = rc;
	return tmp;
}

//根据扩展二叉树的先根序列创建二叉树
lrpTree create_lrpTree(string str, int& idx) {
	lrpTree ret;
	if (str[idx] == '#' || idx == str.size()) {
		idx++;
		return NULL;
	}
	ret = new lrpNode;
	ret->data = str[idx++];
	//通过递归更新ret的位置
	ret->lc = create_lrpTree(str, idx);  //创建ret的左子树，直到#结束
	ret->rc = create_lrpTree(str, idx);	 //创建ret的右子树，直到#结束
	return ret;
}

/*
	二叉树的遍历
	二叉树的遍历是指按某种顺序访问二叉树中的结点，每个结点都被访问且访问一次。
	遍历也是二叉树进行其他运算的基础。
*/

// 先根遍历：即首先先访问根结点，然后先根遍历左子树，最后先跟遍历右子树。
// 顺序：ABDEGCFH
// 递归算法
void preOrder(lrpTree rt) {
	if (rt == NULL)return;
	cout << rt->data; // 访问当前结点
	preOrder(rt->lc); // 先根遍历左子树
	preOrder(rt->rc); // 后根遍历右子树
}

// 利用递归方法实现先根遍历的代码清晰易懂，但当树的高度较大时，递归的层次较高，甚至可能会造成爆栈。
// 为了避免该情况，可以采用非递归方法实现二叉树的先根遍历，非递归用栈来模拟函数递归过程
// 左右每边遍历完后，栈都为空的状态;
// 每一个结点都要考虑右结点，所以每个都会被top，top后即失去了所有价值，需pop掉
// 先根遍历的非递归算法
void preOrder1(lrpTree rt) {
	stack<lrpTree>stk;
	lrpTree t = rt;
	while (t || !stk.empty()) {
		while (t) {  //输出t，并沿t的左分支向下遍历，直到没有
			cout << t->data;
			stk.push(t);
			t = t->lc;
		}
		t = stk.top();
		stk.pop();
		t = t->rc;  //考虑栈顶元素的右分支
	}
}

//中根遍历：首先中根遍历左子树，然后访问根节点，最后中根遍历右子树
//顺序：DBGEAFHC
//递归算法
void midOrder(lrpTree rt) {
	if (rt == NULL)return;
	midOrder(rt->lc);
	cout << rt->data;
	midOrder(rt->rc);
}

//后根遍历：首先后根遍历左子树，然后后根遍历右子树，最后访问根节点
//顺序：DGEBHFCA
//递归算法
void postOrder(lrpTree rt) {
	if (rt == NULL)return;
	postOrder(rt->lc);
	postOrder(rt->rc);
	cout << rt->data;
}
 
//为了检查所构建的二叉树是否正确，可将二叉树的每个结点的数据输出，并输出其两个孩子的数据
void print_lrpTree(lrpTree rt) {
	if (rt == NULL) return;
	cout << rt->data << " ";
	if (rt->lc) cout << "lChind:" << rt->lc->data << " ";
	else cout << "lChind:NULL" << " ";
	if (rt->rc) cout << "rChind:" << rt->rc->data << " "<<endl;
	else cout << "rChind:NULL" << " ";
	print_lrpTree(rt->lc);
	print_lrpTree(rt->rc);
}

int main()
{
	//初始版创建二叉树
	lrpTree t1 = new lrpNode, t2 = new lrpNode, t = new lrpNode;
	//构建左子树
	t1 = create_lrpTree('G',NULL,NULL), t2 = create_lrpTree('E', t1,NULL);
	t1 = create_lrpTree('D',NULL,NULL), t2 = create_lrpTree('B', t1, t2);
	//构建右子树
	t1 = create_lrpTree('H', NULL, NULL), t1 = create_lrpTree('F', NULL, t1);
	t1 = create_lrpTree('C', t1, NULL), t = create_lrpTree('A', t2, t1);

	//扩展二叉树创建先根序列
	string s = "ABD##EG###CF#H###";
	lrpTree prestr = new lrpNode;
	int i = 0;
	prestr = create_lrpTree(s, i);

	//先根遍历
	preOrder(t);
	cout << endl;
	preOrder1(t);
	cout << endl;
	preOrder(prestr);
	cout << endl;
	preOrder1(prestr);
	cout << endl;

	//中根遍历
	midOrder(t);
	cout << endl;

	//后根遍历
	postOrder(prestr);
	cout << endl;

	//print_lrpTree(t);
}

二叉树括号表示法 

 将左右链指针表示的二叉树转化t为括号的二叉树的括号表达式：

//将左右链指针表示的二叉树转化t为括号的二叉树的括号表达式
string convertToBracket(lrpTree t) {
	if (t == NULL)return "";
	return "(" + convertToBracket(t->lc) + t->data + convertToBracket(t->rc) + ")";
}

输出：(((D)B((G)E))A((F(H))C)) 

分析二叉树括号表示法，可得出一下特点：

1.叶结点直接被一对括号所包含 ，如D/G/H

2.如果一个节点有左子树，则其左端的字符为‘）’，如结点A/B/C；如果没有左子树，则其左端字符为‘（’，如结点F

3.如果一个节点有右子树，则其右端的字符为‘（’，如结点A/B/C；如果没有右子树，则其右端字符为‘）’，如结点C/E

4.每一个左括号代表一颗子树结束，且结点被括号所包含的重数与其在二叉树中的层数一致，如A被一层括号包括，为第一层；D/E/F被三重括号包括，为第三层。

 

 注意：图3-7需要配合代码来看，先看代码后看图

//将左右链指针表示的二叉树转化t为括号的二叉树的括号表达式
string convertToBracket(lrpTree t) {
	if (t == NULL) return "";
	return  "(" + convertToBracket(t->lc) + t->data + convertToBracket(t->rc) + ")";
}

//s = convertToBracket(t);
//	cout << s;

//将二叉树的括号表示形式b转化为左右链指针表示形式，结果作为函数的返回值
lrpTree converToTree(string b) {
	lrpTree rt = new lrpNode, lc = new lrpNode, rc = new lrpNode;
	if (b.size() <= 2) return NULL;
	stack<lrpTree>stk;
	for (int i = 1; i < b.size(); i++) {
		if (b[i] == '(') continue; //跳过左括号
		else if (b[i] == ')') { //右括号，构建第一棵子树，并入队
			rc = stk.top(); stk.pop(); //栈中第一个元素为右子树
			rt = stk.top(); stk.pop(); //栈中第二个元素为根结点
			lc = stk.top(); stk.pop(); //栈中第三个元素为左子树
			rt->lc = lc; rt->rc = rc;
			stk.push(rt); //新的子树入队
		}
		else { //结点
			if (b[i-1] == '(') stk.push(NULL);//结点没有左子树
			rt = new lrpNode;
			rt->data = b[i], stk.push(rt);
			if (b[i + 1] == ')') stk.push(NULL);//结点没有右子树
		}
	}
	return stk.top();
}

//s = "(((D)B((G)E))A((F(H))C))";
//	t1 = converToTree(s);
//	preOrder(t1);

 根据二叉树的括号表示法直接求二叉树的后根序列：该算法可用于求一个表达式的逆波兰表达式。

/*
	可以由二叉树的括号形式直接求该二叉树的后根序列。
	由于二叉树的括号表示b为中根序，b[i]=')'表示一颗子树结束，将该子树输出
	如果b[i+1]为结点，则该子树为b[i+1]的左子树，将b[i+1]保存到一个栈中
	再考虑b[i+1]的右子树，当右子树输出后，再输出b[i+1]
*/
//根据二叉树的括号表示法直接求二叉树的后根序列
string postOrder(string b) {
	string ret;
	stack<char>stk;
	for (int i = 0; i < b.size(); i++){
		if (b[i] != ')')  //b[i]为左括号或结点，直接入栈
			stk.push(b[i]);
		else {  //b[i]为右括号
			while (!stk.empty() && stk.top() != '(') //将栈顶的结点加入ret，直到左括号为止
				ret += stk.top(), stk.pop();
			if (!stk.empty())
				stk.pop(); //左括号出栈
		}
	}
	return ret;
}

 层次遍历：

二叉树的层次遍历是从根节点出发，逐层访问二叉树，并且每一层按从左到右的顺序访问每一个结点。层次遍历所得到的结点序列称为层次序列。例如，上面二叉树图的层次遍历序列为ABCDEFGH。

实现层次遍历需要借助队列，实现方法与广度优先探索算法类似。 

参考： 

1.数据结构：树(Tree)【详解】_UniqueUnit的博客-CSDN博客_数据结构树

2. 树（Tree）和二叉树_快到锅里来呀的博客-CSDN博客