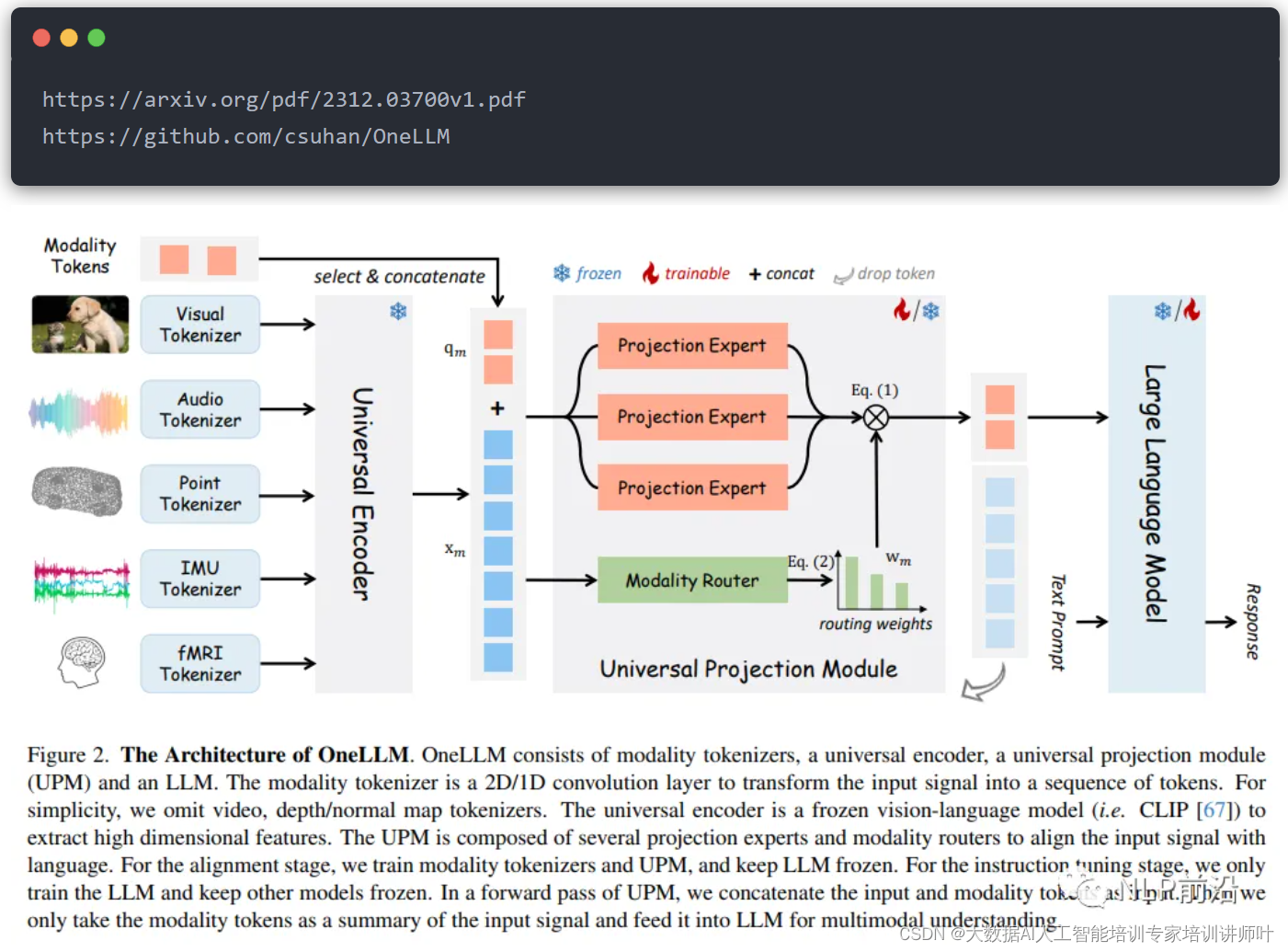
什么是遍历呢？

遍历:按照某种次序把所有结点都访问一遍

先/中/后序遍历:基于树的递归特性确定的次序规则

二叉树的递归特性:

①要么是个空二叉树
②要么就是由“根节点+左子树+右子树”组成的二叉树

先序遍历:根左右（NLR)  ——先访问根结点，在访问左子树，最后访问右子树
中序遍历:左根右(LNR）  ——先访问左子树，在访问根结点，左后放稳右子树
后序遍历:左右根(LRN)    ——先访问左子树，在访问右子树，最后访问根节点

例如：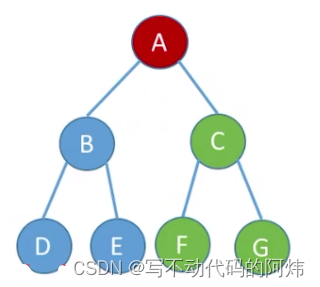

先序遍历:AB DECFG
中序遍历:DB EAFC G

后序遍历:DEBFGCA

EX1: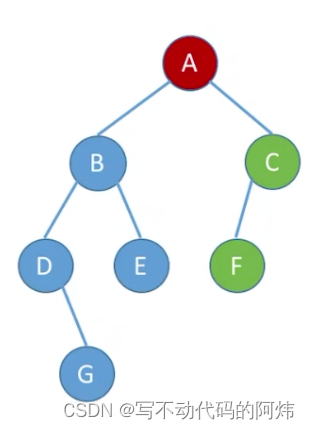

1.先序遍历代码实现：

先序遍历(PreOrder)的操作过程如下：
1.若二叉树为空，则什么也不做;

2.若二叉树非空:

①访问根结点;②先序遍历左子树;③先序遍历右子树。

代码实现：

typedef struct BiTNode{
ElemType data;
struct BiTNode*lchild,*rchild;
}BiTNode,*BiTree;


//先序遍历
void Pre0rder(BiTree T){
    if(T!=NULL){
       visit(T);          //访问根结点
       Pre0rder(T->lchild);      //递归遍历左子树
       Pre0rder(T->rchild) ;    //递归遍历右子树
    }
}

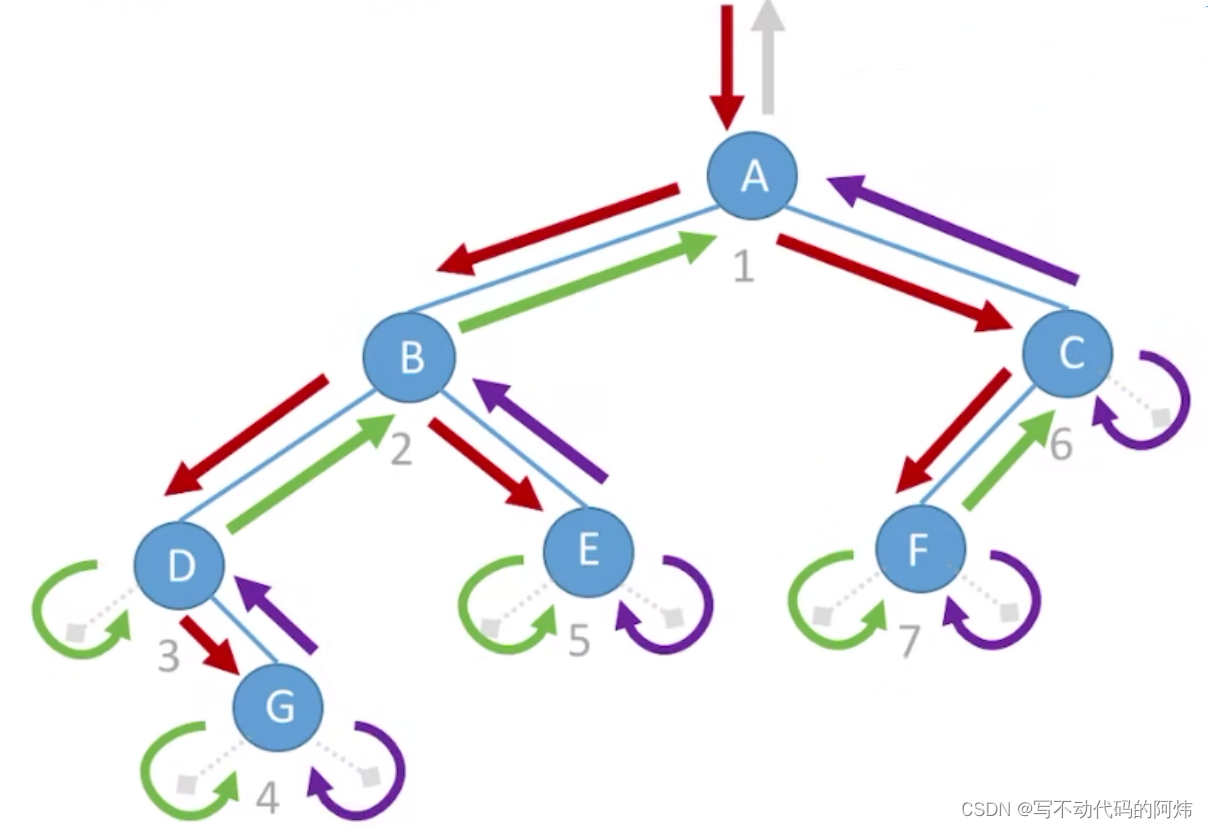
2.中序遍历代码实现：

中序遍历(lnOrder）的操作过程如下:

1.若二叉树为空，则什么也不做;

2.若二叉树非空:
①先序遍历左子树;②访问根结点;③先序遍历右子树。

typedef struct BiTNode{
ElemType data;
struct BiTNode*lchild,*rchild;
}BiTNode,*BiTree;


//中序遍历
void In0rder(BiTree T){
    if(T!=NULL){
       In0rder(T->lchild) ;       //递归遍历左子树
       visit(T);                 //访问根结点
       InOrder(T->rchild) ;      //递归遍历右
    }
}

 

 

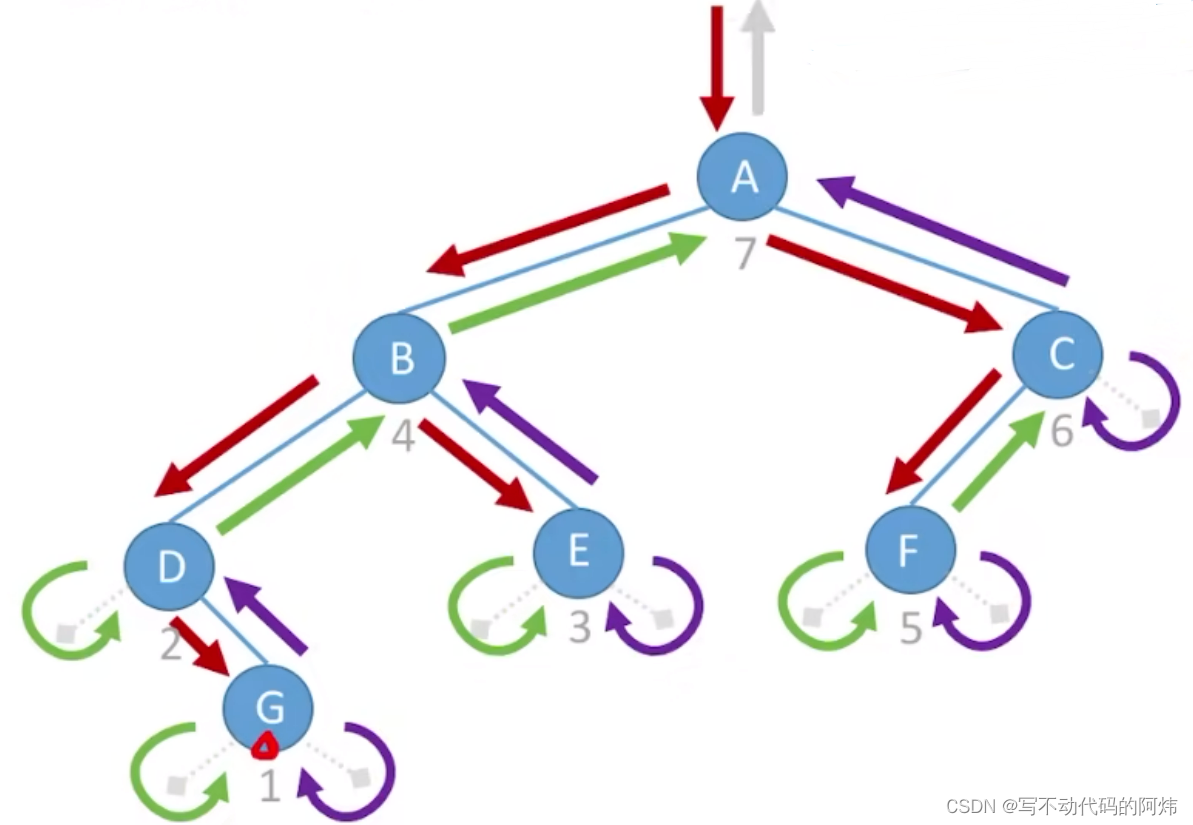
3.后序遍历：
后序遍历( InOrder）的操作过程如下:

1.若二叉树为空，则什么也不做;

2.若二叉树非空:①先序遍历左子树;②先序遍历右子树;③访问根结点。

 

 

 4.求树的深度：

int treeDepth(BiTree T){
    if (T == NULL){
       return 0;
}
    else {
       int l = treeDepth(T->lchild) ;
       int r = treeDepth(T->rchild);
       //树的深度=Max(左子树深度，右子树深度)+1
       return l>r ? l+1 : r+1;
    }
}