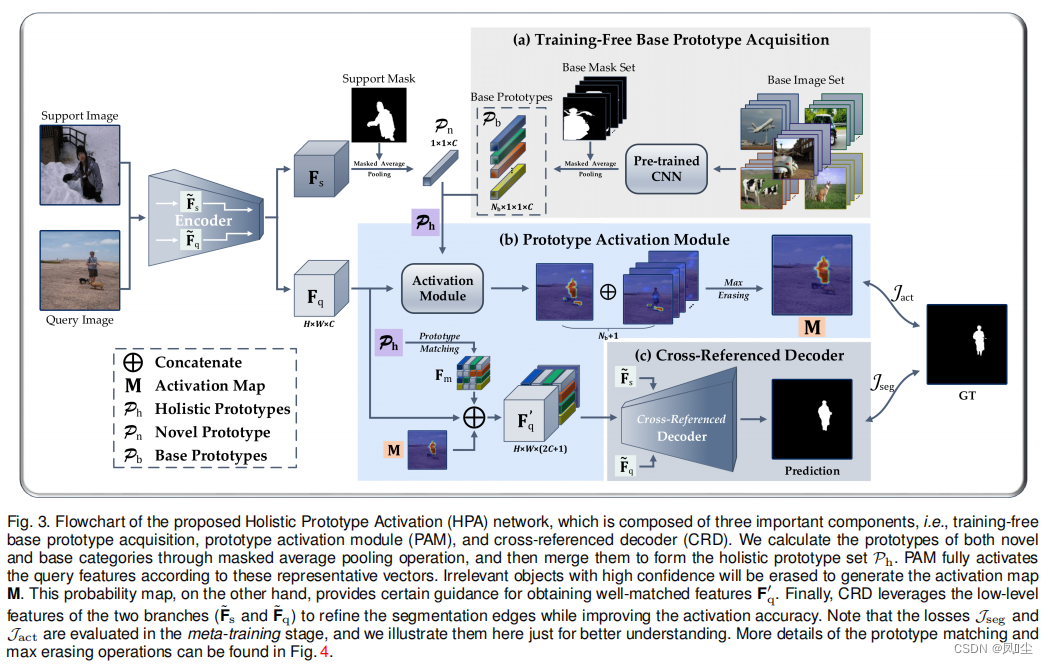
题目描述

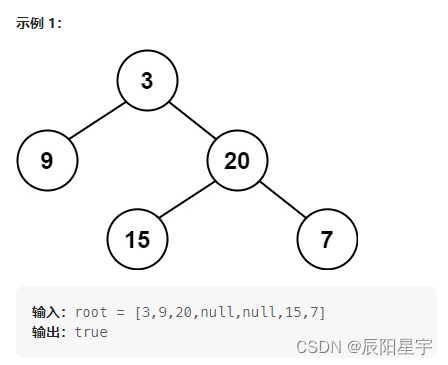
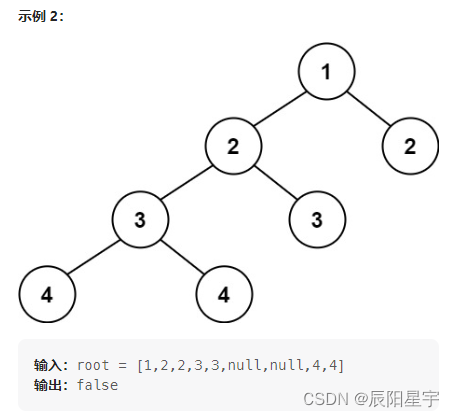
在这里插入图片描述

原题链接：110. 平衡二叉树

解题思路

一、后序遍历（自底向上）

在这里要和 90、【树与二叉树】leetcode ——104. 二叉树的最大深度：层次遍历+DFS+子问题分解（C++版本）这个作比较。

深度，实际上是从上到下，求二叉树的路径，对应的为先序遍历。
高度，实际上是从下到上，求二叉树的路径，对应的为后序遍历。
当所求结点的高度=深度时，可分别用先序和后序遍历求深度或高度。

对于求高度的题，最适宜的使用后序遍历，自底向上返回信息。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool flag = true;           // flag用于判定是否为平衡二叉树
    int heightTree(TreeNode* root) {
        if(!root)       return 0;
        int leftheight = heightTree(root->left);
        int rightheight = heightTree(root->right);
        if(abs(leftheight - rightheight) > 1) {
            flag = false;       // 当不满足平衡二叉树性质时，变为false
        }
        return max(leftheight, rightheight) + 1;        // 返回当前结点高度
    }

    bool isBalanced(TreeNode* root) {
        heightTree(root);
        return flag;
    }
};

时间复杂度 $O (n)$
空间复杂度 $O (n)$

二、先序遍历（自顶向下）

这个方法并不推荐，需要从上到下每次查看各个结点的高度差是否小于等于1，会将下面的结点重复遍历。

class Solution {
public:
    int height(TreeNode* root) {
        if (root == NULL) {
            return 0;
        } else {
            return max(height(root->left), height(root->right)) + 1;
        }
    }

    bool isBalanced(TreeNode* root) {
        if (root == NULL) {
            return true;
        } else {
            return abs(height(root->left) - height(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
        }
    }
};