【算法刷题 DAY04】剑指offer树3和队列与栈总结

JZ36 二叉搜索树与双向链表

描述

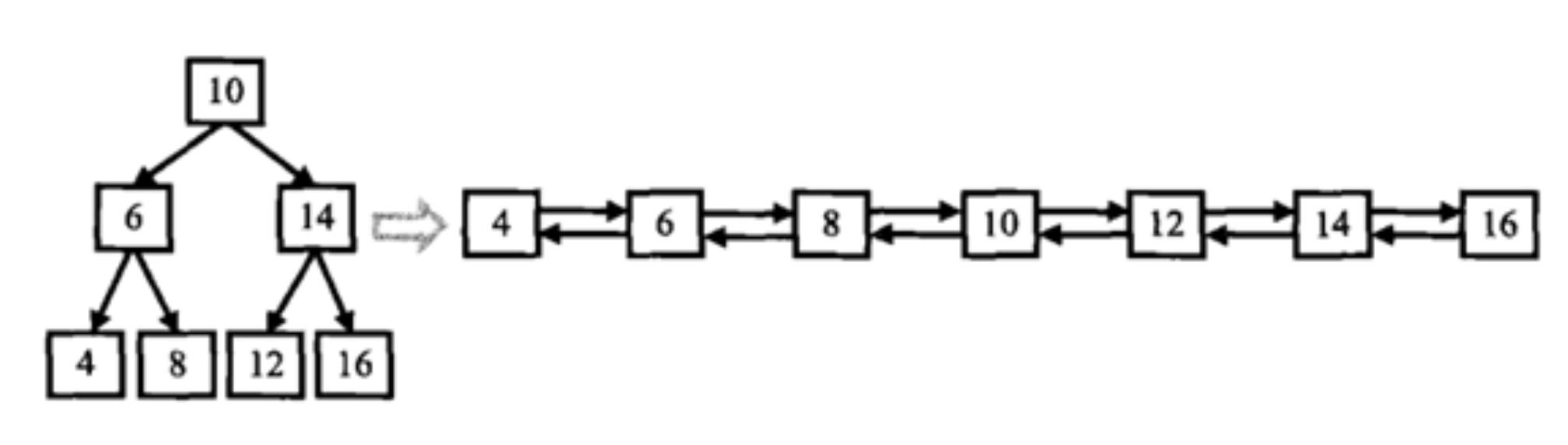
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。如下图所示

注意:
1.要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构

解题思路：

首先对二叉树进行中序遍历，把遍历到的每一个结点都保存到队列中。
然后将第一个元素出队，使用head指针始终指向链表的第一个元素。让pre指针初始化为pre=head。
然后开始循环遍历队列，每出队一个元素，就进行相关的链接操作，知道队列中没有元素为止。

public TreeNode Convert(TreeNode pRootOfTree) {
    // 当结点为空当时候
    if (pRootOfTree == null)
      return null;

    // 中序遍历结点，并将结点存入到队列中
    Queue<TreeNode> queue = new LinkedList<>();
    // 中序遍历
    inorder(pRootOfTree, queue);
    // 从队列中先取出一个结点
    TreeNode head = queue.poll();
    TreeNode pre = head;

    // 循环队列
    while (!queue.isEmpty()) {
      // 取出元素
      TreeNode cur = queue.poll();
      pre.right = cur;
      cur.left = pre;
      pre = cur;
    }
    return head;
}

private void inorder(TreeNode root, Queue<TreeNode> queue) {
    if (root == null)
      return;
    inorder(root.left, queue);
    queue.offer(root);
    inorder(root.right, queue);
}

JZ8 二叉树的下一个结点

描述
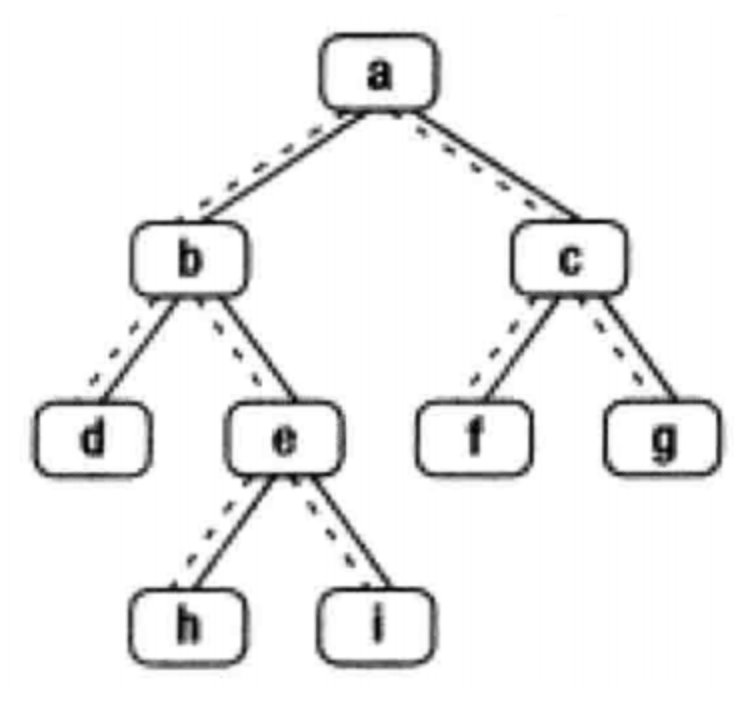
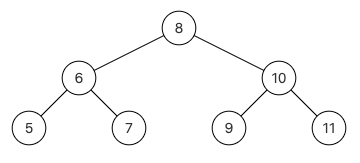
给定一个二叉树其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的next指针。下图为一棵有9个节点的二叉树。树中从父节点指向子节点的指针用实线表示，从子节点指向父节点的用虚线表示

示例:

输入:{8,6,10,5,7,9,11},8

返回:9

解析:这个组装传入的子树根节点，其实就是整颗树，中序遍历{5,6,7,8,9,10,11}，根节点8的下一个节点就是9，应该返回{9,10,11}，后台只打印子树的下一个节点，所以只会打印9，如下图，其实都有指向左右孩子的指针，还有指向父节点的指针，下图没有画出来

解题思路：

首先根据传入结点中的指向父结点的指针，一直向上查找，最终可以查找到二叉树的根结点。
然后对二叉树进行中序遍历，并将结点保存到队列中
遍历队列，每次出队都和传入元素的进行比较，如果相等，则返回目前队列中的第一个元素即可。

public TreeLinkNode GetNext(TreeLinkNode pNode) {
    // 根据传入的结点，通过指向父结点的指针，一直找，最终可以找到这个二叉树的根结点
    if(pNode == null) return null;
    TreeLinkNode root = pNode;
    // 查找根结点
    while (root.next != null) root = root.next;
    Queue<TreeLinkNode> queue = new LinkedList<>();
    // 然后二叉树进行中序遍历，将遍历到的结点保存到队列中
    inorder(root, queue);
    // 循环队列中元素，找到输入元素的下一个元素，然后将结点返回即可
    while (!queue.isEmpty()) {
      TreeLinkNode poll = queue.poll();
      if (poll.val == pNode.val)
        return queue.poll();
    }

    return null;
}

private void inorder(TreeLinkNode root, Queue<TreeLinkNode> queue) {
    if (root == null)
      return;
    inorder(root.left, queue);
    queue.offer(root);
    inorder(root.right, queue);
}

JZ68 二叉搜索树的最近公共祖先

描述

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

1.对于该题的最近的公共祖先定义:对于有根树T的两个节点p、q，最近公共祖先LCA(T,p,q)表示一个节点x，满足x是p和q的祖先且x的深度尽可能大。在这里，一个节点也可以是它自己的祖先.

2.二叉搜索树是若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值

3.所有节点的值都是唯一的。

4.p、q 为不同节点且均存在于给定的二叉搜索树中。

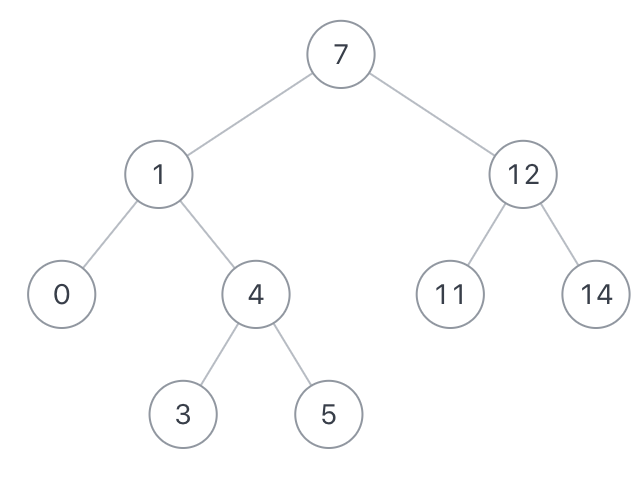
如果给定以下搜索二叉树: {7,1,12,0,4,11,14,#,#,3,5}，如下图:

示例1

输入：

{7,1,12,0,4,11,14,#,#,3,5},1,12

复制

返回值：

复制

说明：

节点1 和 节点12的最近公共祖先是7

示例2

输入：

{7,1,12,0,4,11,14,#,#,3,5},12,11

复制

返回值：

复制

说明：

因为一个节点也可以是它自己的祖先.所以输出12

解题思路1:利用循环

考虑到二叉搜索树的性质，比根小的元素都在左子树，比根大的元素都在右子树上。因此我们可以根据p,q的大小来判断两个结点的位置

当p<root, q<root时，说明两个结点都在root的左子树上，那么应该让root = root.left，然后继续以root.left为根搜索公共祖先
当p>root, q>root时，说明两个结点都在root的右子树上，那么应该让root = root.right，然后继续以root.right为根搜索公共祖先
当p<root, q>root时，说明两个结点位于root的左右子树上，那么最近公共结点就是root

public int lowestCommonAncestor (TreeNode root, int p, int q) {
    // write code here
    if (root == null) return 0;

    while (root != null) {
      if (p < root.val && q < root.val)
        root = root.left;
      else if (p > root.val && q > root.val)
        root = root.right;
      else
        return root.val;
    }
    return 0;
}

解题思路2（利用中序遍历）:可以利用中序遍历，从而记录从根结点到p,q的路径。路径中最后一个相同的结点就是最近的公共祖先。

比如说上面那个树，查找结点12和结点11的最近公共祖先。

结点11的路径是{7, 12, 11} 结点12的路径是{7, 12} 那么这两个序列中最后重复的元素就是12，那么12就是最近公共祖先。

public int lowestCommonAncestor(TreeNode root, int p, int q) {
    // 通过层序遍历记录到p, q结点的路径
    if (root == null) return 0;

    // 创建两个队列
    Queue<TreeNode> nodeQ = new LinkedList<>();
    Queue<ArrayList<Integer>> pathQ = new LinkedList<>();
    ArrayList<ArrayList<Integer>> pathList = new ArrayList<>();

    // 根结点入队
    nodeQ.offer(root);
    pathQ.offer(new ArrayList<>(Arrays.asList(root.val)));

    // 开始遍历
    while (!nodeQ.isEmpty()) {
      // 出队
      TreeNode node = nodeQ.poll();
      ArrayList<Integer> currentPath = pathQ.poll();

      if (node.val == p || node.val == q) {
        pathList.add(currentPath);
      }

      // 判断左右子树
      if (node.left != null) {
        nodeQ.offer(node.left);
        ArrayList<Integer> left = new ArrayList<>(currentPath);
        left.add(node.left.val);
        pathQ.offer(left);
      }

      if (node.right != null) {
        nodeQ.offer(node.right);
        ArrayList<Integer> right = new ArrayList<>(currentPath);
        right.add(node.right.val);
        pathQ.offer(right);
      }
    }

    // 遍历结束后pathList中保存的就是从根到p, q的路径
    ArrayList<Integer> list1 = pathList.get(0);
    ArrayList<Integer> list2 = pathList.get(1);

    // 遍历两个路径
    int i = 0, j = 0;
    int ret = 0;
    while (i < list1.size() && j < list2.size()) {
      if (list1.get(i) == list2.get(j))
        ret = list1.get(i);
      i++;
      j++;
    }

    return ret;
}

第二个方法实际上并没有利用到二叉搜索树的一些特殊性质，直接是按照二叉树的性质来做的。所以第二种方法同时适用于求二叉树中两个结点的最近公共祖先。如下面这道题所示。

JZ86 在二叉树中找到两个节点的最近公共祖先

描述

给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1 和 o2，请找到 o1 和 o2 的最近公共祖先节点。

数据范围：树上节点数满足 1 \le n \le 10^5 \1≤n≤105 , 节点值val满足区间 [0,n)

要求：时间复杂度 O(n)O(n)

注：本题保证二叉树中每个节点的val值均不相同。

如当输入{3,5,1,6,2,0,8,#,#,7,4},5,1时，二叉树{3,5,1,6,2,0,8,#,#,7,4}如下图所示：

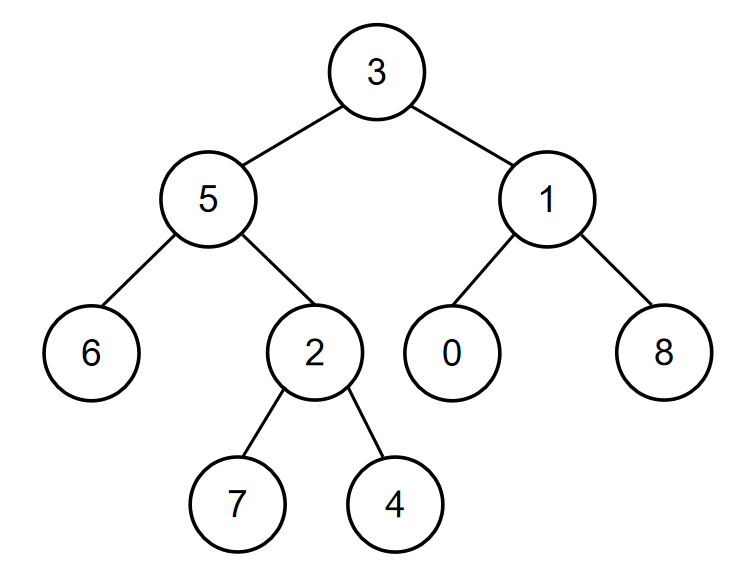
所以节点值为5和节点值为1的节点的最近公共祖先节点的节点值为3，所以对应的输出为3。

节点本身可以视为自己的祖先

解题思路1（利用中序遍历）:可以利用中序遍历，从而记录从根结点到p,q的路径。路径中最后一个相同的结点就是最近的公共祖先。

比如说上面那个树，查找结点12和结点11的最近公共祖先。

结点11的路径是{7, 12, 11} 结点12的路径是{7, 12} 那么这两个序列中最后重复的元素就是12，那么12就是最近公共祖先。

public int lowestCommonAncestor(TreeNode root, int p, int q) {
    // 通过层序遍历记录到p, q结点的路径
    if (root == null) return 0;

    // 创建两个队列
    Queue<TreeNode> nodeQ = new LinkedList<>();
    Queue<ArrayList<Integer>> pathQ = new LinkedList<>();
    ArrayList<ArrayList<Integer>> pathList = new ArrayList<>();

    // 根结点入队
    nodeQ.offer(root);
    pathQ.offer(new ArrayList<>(Arrays.asList(root.val)));

    // 开始遍历
    while (!nodeQ.isEmpty()) {
      // 出队
      TreeNode node = nodeQ.poll();
      ArrayList<Integer> currentPath = pathQ.poll();

      if (node.val == p || node.val == q) {
        pathList.add(currentPath);
      }

      // 判断左右子树
      if (node.left != null) {
        nodeQ.offer(node.left);
        ArrayList<Integer> left = new ArrayList<>(currentPath);
        left.add(node.left.val);
        pathQ.offer(left);
      }

      if (node.right != null) {
        nodeQ.offer(node.right);
        ArrayList<Integer> right = new ArrayList<>(currentPath);
        right.add(node.right.val);
        pathQ.offer(right);
      }
    }

    // 遍历结束后pathList中保存的就是从根到p, q的路径
    ArrayList<Integer> list1 = pathList.get(0);
    ArrayList<Integer> list2 = pathList.get(1);

    // 遍历两个路径
    int i = 0, j = 0;
    int ret = 0;
    while (i < list1.size() && j < list2.size()) {
      if (list1.get(i) == list2.get(j))
        ret = list1.get(i);
      i++;
      j++;
    }

    return ret;
}

JZ9 用两个栈实现队列

描述

用两个栈来实现一个队列，使用n个元素来完成 n 次在队列尾部插入整数(push)和n次在队列头部删除整数(pop)的功能。队列中的元素为int类型。保证操作合法，即保证pop操作时队列内已有元素。

解题思路：

对于入队，只需要将元素保存到stack1中即可
对于出队，首先需要判断一下stack2中是否有元素，如果有元素，则返回栈顶元素即可；如果stack2中没有元素，则需要将stack1中所有元素存入stack2，然后从stack2中弹出一个元素即可。

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();

    public void push(int node) {
        // 入队 就是向stack1中入栈即可
        stack1.push(node);
    }

    public int pop() {
        // 判断stack2中是否有元素
        // 如果有元素，则直接从stack2中出栈一个元素即可
        if (stack2.size() > 0) {
            return stack2.pop();
        }
        // 如果没有元素，则从将stack1中的元素全部压入stack2 然后从stack2中出栈一个元素
        while (!stack1.isEmpty()) {
            // 将stack1中数据保存到stack2
            stack2.push(stack1.pop());
        }
        return stack2.pop();
    }
}

JZ30 包含min函数的栈

描述

定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的 min 函数，输入操作时保证 pop、top 和 min 函数操作时，栈中一定有元素。

解题思路1：在计算栈中元素最小值的时候，依次遍历栈中所有元素，将元素保存到list中。等遍历完毕后，将list求逆序列。然后在循环list，依次保存到stack中。这种方法时间和空间复杂度都很高。这道题的本意肯定不是这样做。但是可以AC。

public class Solution {
    private Stack<Integer> stack = new Stack<>();

    public void push(int node) {
        stack.push(node);
    }

    public void pop() {
        stack.pop();
    }

    public int top() {
        return stack.peek();
    }

    public int min() {
        ArrayList<Integer> list = new ArrayList<>();
        Integer min = Integer.MAX_VALUE;
        while (!stack.isEmpty()) {
            Integer pop = stack.pop();
            if (pop < min) {
                min = pop;
            }
            list.add(pop);
        }
        Collections.reverse(list);
        for (Integer integer : list) {
            stack.push(integer);
        }
        return min;
    }
}

**解题思路2:**利用两个栈来解决。一个栈就是正常的栈，另一个栈用来保存最小值

入栈：stack1正常入栈，stack2需要判断。如果stack2中没有元素则直接入栈。如果有元素，则需要判断stack2的栈顶元素是否大于输入元素，如果满足条件，则stack2也入栈。
出栈。stack1正常出栈，如果此时stack1中出栈元素等于stack2的栈顶元素，那么stack2也出栈
min：stack2的栈顶元素始终是stack1中的最小值。

public class Solution {
    private Stack<Integer> stack1 = new Stack<>();
    private Stack<Integer> stack2 = new Stack<>();

    public void push(int node) {
        // stack1正常入栈
        stack1.push(node);
        // 判断stack2中是否有元素
        if (stack2.isEmpty()) {
            // 为空则直接入栈
            stack2.push(node);
        }
        // 如果不为空，则需要判断stack2的栈顶元素是否小于等于node
        if (stack2.peek().intValue() >= node) {
            stack2.push(node);
        }
    }

    public void pop() {
        if (stack1.peek().intValue() == stack2.peek().intValue()) {
            stack2.pop();
        }
        stack1.pop();
    }

    public int top() {
        return stack1.peek();
    }

    public int min() {
        return stack2.peek();
    }
}

JZ73 翻转单词序列

描述

牛客最近来了一个新员工Fish，每天早晨总是会拿着一本英文杂志，写些句子在本子上。同事Cat对Fish写的内容颇感兴趣，有一天他向Fish借来翻看，但却读不懂它的意思。例如，“nowcoder. a am I”。后来才意识到，这家伙原来把句子单词的顺序翻转了，正确的句子应该是“I am a nowcoder.”。Cat对一一的翻转这些单词顺序可不在行，你能帮助他么？

解题思路1:

利用字符串分割函数，将字符串分解为一个一个的单词组成的数组。
从数组末尾到数组头开始遍历，使用StringBuilder构建字符串。构建过程中需要加空格，最后一个元素不需要加空格。
最终返回即可

public String ReverseSentence(String str) {
    if ("".equals(str))
      return "";
    // 使用空格划分单词
    String[] words = str.split(" ");
    StringBuilder stringBuilder = new StringBuilder();
    for (int i = words.length - 1; i >= 0; i --) {
      stringBuilder.append(words[i]);
      if (i == 0)
        continue;
      stringBuilder.append(" ");
    }
    return stringBuilder.toString();
}

解题思路2（利用栈）：实现顺序反转可以使用栈。

利用字符串分割函数，将字符串分解为一个一个的单词组成的数组。
将数组每一个元素入栈。每一个单词入栈以后，在入栈一个空格。
循环出栈之前，先将最后添加的那个空格删除掉。
出栈，使用StringBuilder构建字符串。

public String ReverseSentence(String str) {
    if ("".equals(str)) return "";
    Stack<String> stack = new Stack<>();
    String[] words = str.split(" ");
    for (String word : words) {
      stack.push(word);
      stack.push(" ");
    }
    // 移除栈顶的空格
    stack.pop();

    StringBuilder stringBuilder = new StringBuilder();
    while (!stack.isEmpty()) {
      stringBuilder.append(stack.pop());
    }
    return stringBuilder.toString();
}

JZ31 栈的压入、弹出序列

描述
输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。

注意：同时满足压入和弹出序列的情况只有一种

解题思路：

建立一个辅助栈，遍历入栈序列。每遍历一个元素，就入栈。

元素入栈后，需要判断一下栈顶元素是否和popA中指定位置的元素相同，如果相同，则元素出栈。

整个循环结束后，如果栈中还有元素，说明不满足条件。

public boolean IsPopOrder(int [] pushA,int [] popA) {
    if (pushA == null || pushA.length == 0)
      return false;

    Stack<Integer> stack = new Stack<>();
    int k = 0;
    // 遍历入栈序列
    for (int i = 0; i < pushA.length; i++) {
      // 入栈
      stack.push(pushA[i]);
      // 判断栈顶元素是否和popA中元素相同
      while (!stack.isEmpty() && stack.peek() == popA[k]) {
        stack.pop();
        k++;
      }
    }
    return stack.isEmpty();
}