堆排序

时间复杂度：O(N*logN)
稳定性：不稳定（相同元素排序后的相对位置改变）

堆

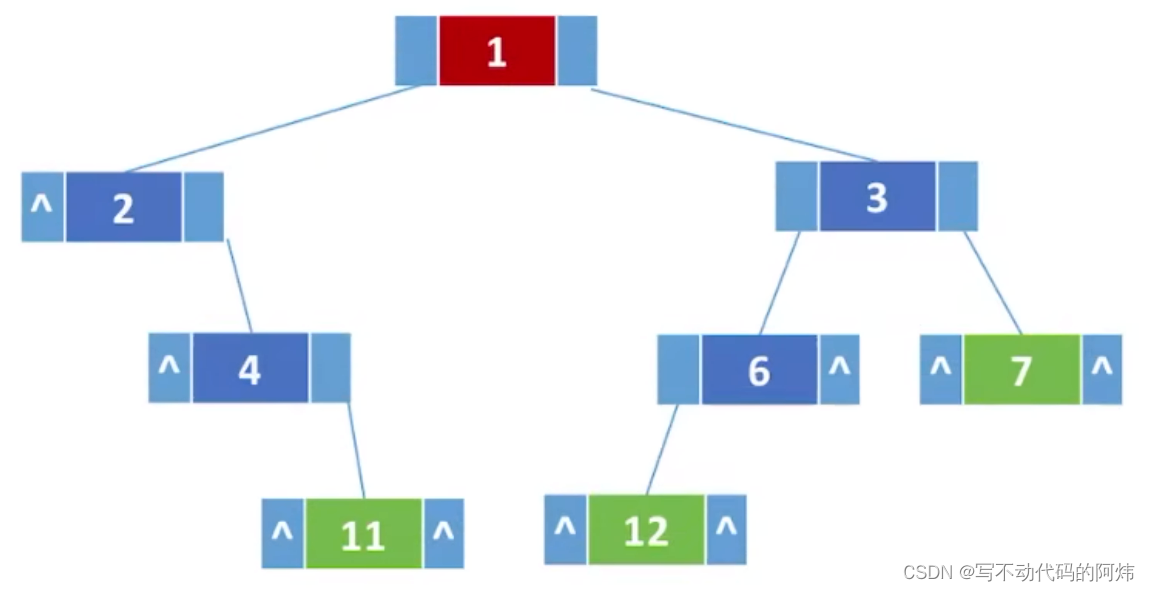
堆的逻辑结构是一棵完全二叉树；堆的物理结构是一个数组，通过下标表示父子结点的关系

这个数组的元素是按照层序遍历（广度优先）的方式存储的。

以下左图为例，其堆的数组元素为 { 6 ，8，10，12，14，16，18 }

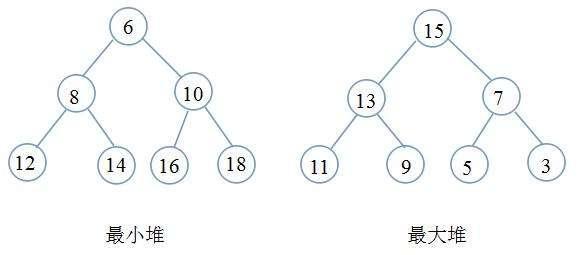
以下parent、child、leftchild、rightchild均为下标值 （这些公式表示的是父子结点的关系）

• parent = (child - 1) / 2
• leftchild = parent * 2 + 1
• rightchild = parent * 2 + 2

堆的两个特性：

1. 结构性： 用数组表示一棵完全二叉树
2. 有序性： 任一结点的关键字是其子树所有节点的最大值（或最小值）。
“最大堆”，也称“大顶堆”（或“大根堆”），简称大堆。特点是：父亲大于等于孩子
“最小堆”，也称“小顶堆”（或“小根堆”），简称小堆。特点是：父亲小于等于孩子

了解到这，考虑一个问题，假设有一个深度为4的小堆，那么深度为2的那一层的每一个数据一定都小于深度为3的那一层的每一个元素吗？

不一定，堆的特性规定，只要每个父亲大于（或小于）自己的孩子即可，不需要大于（或小于）同层父亲的孩子。

思路过程

建堆

向下调整算法

前提：左右子树必须同为大堆或小堆
结果：将对象插入到二叉树中，使得插入后的二叉树满足堆的特性

以小堆为例， 父亲跟它的左右孩子的较小值比较，如果父亲比较小值大，那么交换较小孩子和父亲，父亲的值不变位置变化，然后继续和现在位置的左右孩子的较小值比较，父亲大继续交换，直到叶子节点终止（这是算法终止的第一种情况）。如果在到达叶子节点前，出现父亲比左右孩子较小值还要小的情况，那么不执行交换，终止算法执行（第二种终止情况）。

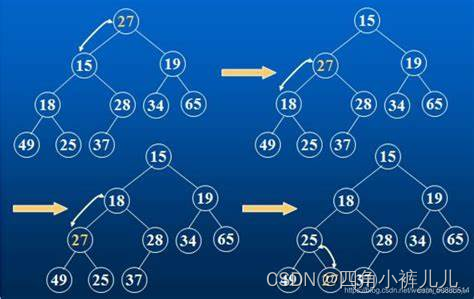
以大堆为例， 父亲跟它的左右孩子的较大值比较，如果父亲比较大值小，那么交换较大孩子和父亲，父亲的值不变位置变化，然后继续和现在位置的左右孩子的较大值比较，父亲小继续交换，直到叶子节点终止（这是算法终止的第一种情况）。如果在到达叶子节点前，出现父亲比左右孩子较大值还要大的情况，那么不执行交换，终止算法执行（第二种终止情况）。

如果逻辑上的完全二叉树不满足前提条件（根节点开始），怎么办?

既然对根节点没法使用向下调整算法，我们不妨从树的其他满足前提条件的结点开始使用向下调整算法。

从哪些结点开始使用向下调整算法？从叶子结点?

叶子节点没有左右孩子，那么默认就是一个小堆（或大堆），没必要对它使用向下调整算法。

因此，我们开始使用向下调整算法的结点是倒数第一个非叶子节点，然后将下标减1，就是倒数第二个非叶子节点，以此类推，结果建堆成功。

怎么找到倒数第一个非叶子结点？

堆数组最后一个元素是逻辑完全二叉树的最右边的叶子节点，它的父亲就是倒数第一个非叶子结点。

最右边的叶子节点的在数组中的下标是len - 1（len是数组的元素个数），要找它的父亲，用到父子结点关系公式：parent = (child - 1) / 2

代入得到倒数第一个非叶子节点对应的下标值：(len - 1 - 1) / 2

排序

建堆的过程了解了，假如我要排升序，那么我该建大堆还是小堆？

第一反应就是建小堆，最小数在堆顶，堆的物理结构是数组，当我们把第一个元素（建小堆后第一个元素是序列中的最小元素）拿出来后，之后需要在剩下的数中再去选数，但是剩下的树的结构都乱了，需要重新建堆才能选出下一个数，建堆的时间复杂度为O(N)，这样反复建堆可以实现排序的目的，不过堆排序就失去了效率优势。

所以我们排升序需要建大堆，最大数在堆顶，每次取堆顶元素，与末尾元素交换，比如：某个序列建大堆后数组元素顺序为：{ 9，8，6，7，3，2，1，5，4，0 }，9是堆顶元素，将堆顶元素取出来与0元素交换，得到{ 0，8，6，7，3，2，1，5，4，9 }，9是最大元素，不需要再参与排序，除去9后前 len - 1 个元素可以执行向下调整算法，0的左右子树都是大堆，算法执行完毕后，次大的元素到达堆顶，将次大的元素与倒数第二个元素交换，此时倒数一二个元素已经不需要参与排序，以此类推，便实现了顺序堆排序。

代码实现

void Swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}

//每趟向下调整算法
void AdjustDown(int* a, int len, int root)
{
    //一次向下调整算法
    int parent = root;
    //假设左孩子大于右孩子,child存储值较大的孩子的下标
    int child = parent * 2 + 1;
    while (child < len)
    {
        if (child + 1 < len && a[child] < a[child + 1])//语句child + 1 < n用于应对某个父亲只有左孩子的情况
        {
            child++;
        }
        if (a[child] > a[parent])
        {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}


//堆排序
void HeapSort(int* a, int len)
{
    //实现顺序，建大堆
    for (int i = (len - 1 - 1) / 2; i >= 0; i--)
    {
        AdjustDown(a, len, i);
    }
    //排序
    int j = len - 1;
    while (j > 0)
    {
        Swap(&a[0], &a[j]);
        AdjustDown(a, j, 0);
        --j;
    }

}

我们测试一下：

void TestHeapSort()
{
    int a[] = { 2,4,6,4,1,1,8,4,2,0 };
    int len = sizeof(a) / sizeof(int);
    HeapSort(a, len);
    Print(a, len);
}
int main()
{
    TestHeapSort();
    return 0;
}

---