• 前文：模型预测控制MPC（1）—— 基础概念
• 参考：模型预测控制（2022春）
• 本文从偏控制的角度介绍无约束线性MPC方法，$x,u,J$ 分别代表状态、动作和代价函数

---

1. 问题定义

• 考虑一个离散线性时不变多输入输出系统（离散指时间离散，线性指系统动态可由线性方程描述，时不变指系统动态不随时间变化），环境转移如下
  $$x(k+1)=Ax(k)+Bu(k),x\in {\mathbb{R}}^n,u\in {\mathbb{R}}^p$$ 由于是时不变系统，要求 $A,B$ 是稳定的（stabilizable）常数矩阵，现在假设不存在对状态或动作的约束
• 定义 $x(i|k),u(i|k)$ 表示从时刻 $k$ 开始后第 $i$ 步的预测状态和动作。特别地，有 $x(0|k)=x(k),u(0|k)=u(k)$

1.1 多步预测公式

• 在系统已知的情况下，可以如下进行多步预测
  $$\begin{array}{rl}x(1\mid k)& =Ax(0\mid k)+Bu(0\mid k)\\ x(2\mid k)& =Ax(1\mid k)+Bu(1\mid k)=A[Ax(0\mid k)+Bu(0\mid k)]+B(1\mid k)\\ & =A^{2}x(0\mid k)+ABu(0\mid k)+Bu(1\mid k)\\ & ⋮⋮⋮\\ x(i\mid k)& =Ax(i-1\mid k)+Bu(i-1\mid k)=\cdots \\ & =A^{i}x(0\mid k)+A^{i-1}Bu(0\mid k)+A^{i-2}Bu(1\mid k)+\cdots +Bu(i-1\mid k)\end{array}$$ 设预测时间步数为 $N$，多步预测结果可以写成更紧凑的矩阵形式
  $$\begin{gathered} X(k)=Fx(k)+\Phi U(k)\text{where} \\ X(k)\triangleq \left[\begin{array}{c}x(1\mid k)\\ x(2\mid k)\\ ⋮\\ x(N\mid k)\end{array}\right]U(k)\triangleq \left[\begin{array}{r}u(0\mid k)\\ u(1\mid k)\\ ⋮\\ u(N-1\mid k)\end{array}\right] \\ F=\left[\begin{array}{l}A\\ A^2\\ ⋮\\ A^N\end{array}\right]\Phi =\left[\begin{array}{llll}B& 0& & \\ AB& B& 0& \\ ⋮& & & \\ A^{N-1}B& A^{N-2}B& \cdots & B\end{array}\right] \end{gathered}$$ 其中 $X$ 和 $U$ 分别为状态序列和动作序列，$F,\Phi$ 是由环境模型确定的常数矩阵

1.2 代价函数

• 首先把控制系统的示意图绘制如下
  

  在每个时刻 $k$，由控制器产生动作 $u(k)$ 输入被控系统，观测到系统转移至状态 $x(k)$，在下一时刻计算其与参考值（目标）$c(k)$ 的误差 $e(1|k)$ 作为反馈。控制目标通常有两个

  1. 最优追踪效果：最小化控制过程的总误差，即最小化 mse 损失 ${\sum }_{i=1}^N{e}^2(i|k)$，$c\equiv 0$ 时为 ${\sum }_{i=1}^N{x}^2(i|k)$
  2. 最小控制能耗：最小化控制过程的总输入，即最小化 mse 损失 ${\sum }_{i=1}^N{u}^2(i-1|k)$

• 通常使用两个可调节的参数 $q,r$ 权衡两个目标损失，从而构造代价函数。单输入输出系统下形如
  $$J(k)=\sum _{i=1}^{N}q{x}^2(i|k)+r{u}^2(i-1|k)$$ 多输入输出系统下形如（这里使用某种二范数作为 mse 损失的广义形式），是两个二次型之和
  $$\begin{array}{l}J(k)={\sum }_{i=1}^N\Vert x(i\mid k){\Vert }_Q^2+\Vert u(i-1\mid k){\Vert }_R^2=X^T(k)\mathcal{Q}X(k)+U(k{)}^T\mathcal{R}U(k)\text{where}\\ \\ \mathcal{Q}=\left[\begin{array}{llll}Q& & & \\ & Q& & \\ & & \ddots & \\ & & & Q\end{array}\right]\mathcal{R}=\left[\begin{array}{llll}R& & & \\ & R& & \\ & & \ddots & \\ & & & R\end{array}\right]\end{array}$$

• 由 1.1 节有 $X(k)=Fx(k)+\Phi U(k)$，代入有
  $$\begin{array}{rl}J(k)& =(Fx(k)+\Phi U(k){)}^T\mathcal{Q}(Fx(k)+\Phi U(k))+U^T(k)\mathcal{R}U(k)\\ & =x^T(k)F^T\mathcal{Q}Fx(k)+2x^T(k)F^T\mathcal{Q}\Phi U(k)+U^T(k)\left({\Phi }^T\mathcal{Q}\Phi +\mathcal{R}\right)U(k)\end{array}$$

2. 求解优化问题

• 我们在 1.1 节给出了环境模型已知情况下多步预测结果的数学表达式，然后基于它在 1.2 节给出了每一时刻 $k$ 要求解的优化问题表达式，本节考虑如何求解这个优化问题

• 首先回顾代价函数表达式
  $$J(k)=x^T(k)F^T\mathcal{Q}Fx(k)+2x^T(k)F^T\mathcal{Q}\Phi U(k)+U^T(k)\left({\Phi }^T\mathcal{Q}\Phi +\mathcal{R}\right)U(k)$$ 注意式子中 $x$ 是测量得到的反馈，$F,\mathcal{Q},\mathcal{R}$ 都是常数矩阵，我们只能通过优化动作序列 $U$ 来优化 $J$。令 $J$ 关于 $U$ 的梯度为 0，求解最优动作序列 $U^{\ast }$
  $$\begin{array}{rl}& {{\nabla }_U|}_{U=U^{\ast }}={\frac{\partial J}{\partial U}|}_{U=U^{\ast }}=0\\ & \\ & 2x(k{)}^T{F}^T\mathcal{Q}\Phi +{2U(k{)}^T\left({\Phi }^T\mathcal{Q}\Phi +\mathcal{R}\right)|}_{U(k)=U^{\ast }}=0\\ & \\ & U^{\ast }(k)=-{\left({\Phi }^T\mathcal{Q}\Phi +\mathcal{R}\right)}^{-1}{\Phi }^T\mathcal{Q}Fx(k)\end{array}$$
  注意这里要求 $\left({\Phi }^T\mathcal{Q}\Phi +\mathcal{R}\right)$ 可逆，有两种情况

  1. $\mathcal{R}$ 正定，$\mathcal{Q}$ 半正定

     此时 ${\Phi }^T\mathcal{Q}\Phi$ 半正定，它和正定矩阵之和一定正定，正定矩阵可逆

  2. $\mathcal{R}$ 正定或半正定，$\mathcal{Q}$ 正定且 $\Phi$ 是满秩的

     此时 ${\Phi }^T\mathcal{Q}\Phi$ 正定，它和正定或半正定矩阵之和一定正定，正定矩阵可逆。$\Phi$ 的形式第1节已经给出，当 $A,B$ 完全可控时它满秩

  最后，利用一个方块单位阵把最优动作序列 $U^{\ast }(k)$ 中的第一个动作 $u^{\ast }(k)$ 取出来，就得到 $k$ 时刻需要执行的最优动作
  $$u^{\ast }(k)=-\left[\begin{array}{llll}{I}_{p\times p}& 0& \cdots & 0\end{array}\right]{\left({\Phi }^T\mathcal{Q}\Phi +\mathcal{R}\right)}^{-1}{\Phi }^T\mathcal{Q}Fx(k)=-K_{mpc}x(k)$$

  下面给出一个计算最优动作的示例。注意到无约束线性MPC不需要每步在线解优化问题，直接代入以上解析式计算即可
  

• 我们直接算出了 $U^{\ast }(k)={\mathrm{argmin}}_{U}J(k)$ 的解析解。观察 $u^{\ast }(k)$ 的表达式，其中 $\Phi ,x,F,\mathcal{Q},\mathcal{R}$ 都是常值矩阵，因此 $K_{mpc}$ 也是常值矩阵，故 $u^{\ast }(k)$ 就是当前状态 $x(k)$ 的一个线性反馈，我们可以利用这一点验证系统的稳定性

3. 系统稳定性

3.1 有限预测时域

• 把第 2 节得到的最优动 $u^{\ast }(k)=-K_{mpc}x(k)$ 作带回到环境模型 $x(k+1)=Ax(k)+Bu(k)$，得到每步都执行最优动作下的环境转移为
  $$x(k+1)=(A-B{K}_{mpc})x(k)$$ 这是一个离散的线性闭环系统，线性系统的稳定性判别准则如下
  
  如图所示，我们只需要检查 $A-B{K}_{mpc}$ 的特征值是否在单位圆内即可

  前提是要求 $A,B$ 是稳定的，这样 $K_{mpc}$ 才存在

• 对于本文考虑的无约束线性 MPC 而言，使代价函数的最优的动作策略无法保证系统稳定

  系统的稳定性是指系统在受到外部扰动或初始条件变化时，系统的状态不会无限制地增长或衰减，而是会在某个有限的范围内保持。换句话说，稳定的闭环系统会在一定的条件下保持一种平衡状态，而不会发散或者偏离目标（简单说就是状态 $x$ 能否在扰动下收敛）

• 无约束线性 MPC 无法保证稳定性的原因，直观上可以理解为它建模的轨迹和优化的动作序列都是有限长度的，而对有限长度的轨迹预测可能无法真实地反映系统运动趋势，换句话说，随着预测时域 $N$ 减少，更可能出现不稳定问题，如下例所示
  

3.2 无限预测时域

• 当我们优化无限长度的动作序列，即 $N=\infty$ 时，系统的稳定性是可以保证的（证明略）

• 但是，简单地令 $N=\infty$ 会出现问题，虽然依然可以按第 2 节解出
  $$u^{\ast }(k)=-\left[\begin{array}{llll}{I}_{p\times p}& 0& \cdots & 0\end{array}\right]{\left({\Phi }^T\mathcal{Q}\Phi +\mathcal{R}\right)}^{-1}{\Phi }^T\mathcal{Q}Fx(k)=-K_{mpc}x(k)$$ 但此时 $\Phi ,F,\mathcal{Q},\mathcal{R}$ 都是无限维了，这样我们就没法写程序来计算了。为了处理这个问题，我们要利用线性系统的性质：线性系统在最优代价函数关于时域的极限存在且有限，可以写作
  $$J(k)=\sum _{i=1}^{\infty }\Vert x(i\mid k){\Vert }_Q^2+\Vert u(i-1\mid k){\Vert }_R^2=\Vert x(k){\Vert }_P^2-\Vert x(k){\Vert }_Q^2$$ 为了证明这里的第二个等号，需要用到离散形式的李雅普诺夫方程的一个结论：

  给定任意使得离散系统 $x(k+1)=(A-BK)x(k)$ 稳定的矩阵 $K$ 和任意正定对称矩阵 $Q$，一定存在唯一的正定对称矩阵 $P$ 使得下式成立
  $$P-(A-BK{)}^{T}P(A-BK)=Q+K^{T}RK\text{ with }|\mathrm{eig}(A-BK)|<1$$

  接下来利用以上结论证明无穷时域下最优代价函数 $J(k)=\Vert x(k){\Vert }_P^2-\Vert x(k){\Vert }_Q^2$
  $$P-(A-BK{)}^{T}P(A-BK)=Q+K^{T}RK\text{ with }|\mathrm{eig}(A-BK)|<1$$

  Proof：
  $$\begin{array}{rl}& x^T\left[P-(A-BK{)}^{T}P(A-BK)\right]x=x^T\left[Q+K^{T}RK\right]x\\ & x^{T}Px-x^T(A-BK{)}^{T}P(A-BK)x=x^{T}Qx+x^T{K}^{T}RKx\\ & x(k{)}^{T}Px(k)-x^T(k+1)Px(k+1)=x^T(k)Qx(k)+u^T(k)Ru(k)\\ & \Vert x(k){\Vert }_P^2=\sum _{i=k}^{\infty }\Vert x(i){\Vert }_Q^2+\Vert u(i){\Vert }_R^2=\sum _{i=1}^{\infty }\Vert x(i|k){\Vert }_Q^2+\Vert u(i|k){\Vert }_R^2\\ & \Vert x(k){\Vert }_P^2-\Vert x(k){\Vert }_Q^2=\sum _{i=1}^{\infty }\Vert x(i|k){\Vert }_Q^2+\Vert u(i-1|k){\Vert }_R^2\end{array}$$

  1. 第 3 行等号左边用到离散系统转移 $x(k+1)=(A-BK)x(k)$
  2. 第 3 行等号右边用到 $u(k)=-Kx(k)$
  3. 由于 $x$ 和 $u$ 都定义为列向量，$x(k{)}^{T}Px(k)=x^2(k)P,u^T(k)Ru(k)=u^2(k)R$
  4. 第 4 行就是把第 3 行左右都从 $k$ 时刻到 $\infty$ 求和，左边是 $x^2(k)P-x^2(k+1)P+x^2(k+1)P-x^2(k+2)P...$，这样后面全都加减相消了，只留下第一项 $x^2(k)P=\Vert x(k){\Vert }_P^2$

• 证明以上结论后，我们可以通过以下步骤，求解无限预测时域下的最优动作了：要求 $A,B$ 稳定，给定对称正定的 $Q$

  1. 找到任意线性反馈 $u=-Kx$ 使得离散系统稳定（即 $|\text{eig}(a-BK)|<1$）
  2. 根据 $Q,R,K$ 求解李雅普诺夫方程 $P-(A-BK{)}^{T}P(A-BK)=Q+K^{T}RK$，解得正定对称矩阵 $P$
  3. 无限时域下的代价函数值可以如下转换，用有限时域内的代价函数值表示
     $$\begin{array}{rl}J(k)& =\sum _{i=1}^{\infty }\Vert x(i\mid k){\Vert }_Q^2+\Vert u(i-1\mid k){\Vert }_R^2\\ & =\sum _{i=N}^{\infty }\Vert x(i\mid k){\Vert }_Q^2+\Vert u(i-1\mid k){\Vert }_R^2+\sum _{i=1}^{N-1}\Vert x(i\mid k){\Vert }_Q^2+\Vert u(i-1\mid k){\Vert }_R^2\\ & =\Vert x(N\mid k){\Vert }_P^2-\Vert x(N\mid k){\Vert }_Q^2+\sum _{i=1}^{N-1}\Vert x(i\mid k){\Vert }_Q^2+\Vert u(i-1\mid k){\Vert }_R^2\\ & =X^T(k)\mathcal{Q}X(k)+U(k{)}^T\mathcal{R}U(k)\end{array}$$ 注意第三行中减去一个 $x$ 关乎 $Q$ 的二次型，增加一个 $x$ 关乎 $P$ 的二次型，这可以体现在矩阵 $\mathcal{Q}$ 中，而 $\mathcal{R}$ 不变，即
     $$\begin{gathered} \mathcal{Q}=\text{diag}[Q,Q,....,Q,P] \\ \mathcal{R}=\text{diag}[R,R,....,R,R] \end{gathered}$$
  4. 优化 3 中 $J(k)$ 得到的控制策略一定可以保证系统稳定性，优化问题求解过程和第 2 节相同，最优策略为
     $$u^{\ast }(k)=-\left[\begin{array}{llll}{I}_{p\times p}& 0& \cdots & 0\end{array}\right]{\left({\Phi }^T\mathcal{Q}\Phi +\mathcal{R}\right)}^{-1}{\Phi }^T\mathcal{Q}Fx(k)=-K_{mpc}x(k)$$

• 下面给出一个根据以上方法计算的例子

  

• 进一步地，我们可以考察以上第 3 步中对时间划分时 $N$ 不同取值的影响，如下

  
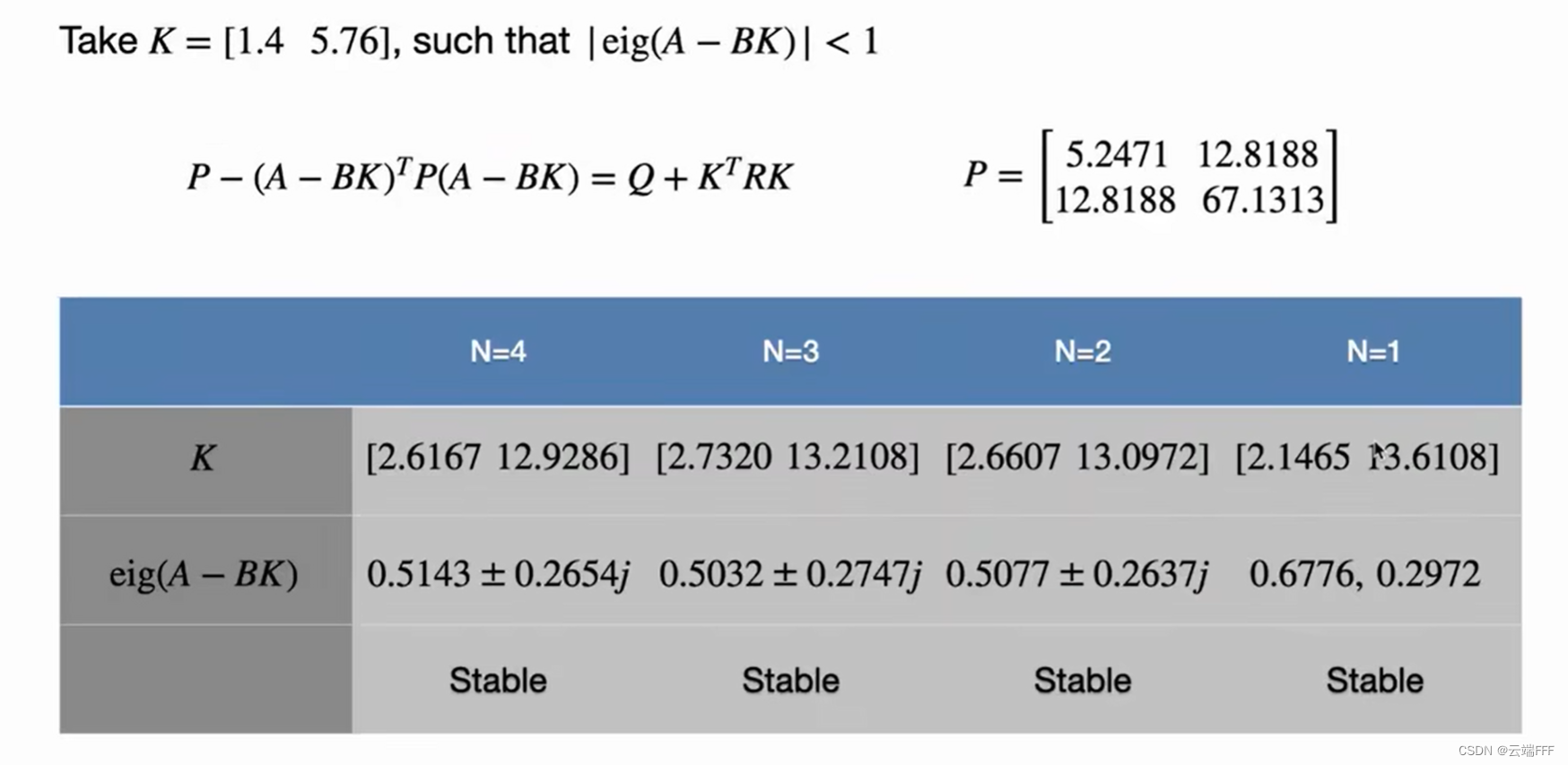
  分析以上计算过程，我们起初任取的 $K$ 从序列第 $N$ 个时刻起才开始发挥作用，因此 $N$ 取值越大，计算结果越接近真实最优值，初始取值的影响越小

4. 无约束线性 MPC 和 LQR

• 无穷时域上，无约束线性MPC和LQR的求解结果其实是一样的
  1. 无约束线性 MPC 通过找到最优的动作序列 { u ( k ) , u ( k + 1 ) . . . } \{u(k), u(k+1)...\} {u(k),u(k+1)...} 来最小化代价函数，这等价于优化 $u=-K_{mpc}x$
  2. LQR 通过求解每一步最优的控制增益 $K_{lqr}$，构造动作 $u=-K_{lqr}x$ 执行来最小化代价函数，这等价于求解最优动作序列 { u ( k ) , u ( k + 1 ) . . . } \{u(k), u(k+1)...\} {u(k),u(k+1)...}
• 因此，二者的优化目标其实是一样的，二者的优化结果也是一样的。但是无约束线性 MPC 仍有意义
  1. 有些场景下我们只关注有限时域内的控制过程，这时 LQR 没法解
  2. 约束 MPC 的稳定性分析是基于无约束 MPC 稳定性分析的