交叉熵是信息论中的一个重要概念,它的大小表示两个概率分布之间的差异,可以通过最小化交叉熵来得到目标概率分布的近似分布。
为了理解交叉熵,首先要了解下面这几个概念。
自信息
信息论的基本想法是,一个不太可能的事件发生了的话,要比一个非常可能发生的事件提供更多的信息。
如果想通过这种想法来量化信息,需要满足以下性质:
- 非常可能发生的事件信息量比较少,并且极端情况下,确定能够发生的事件没有信息量。
- 较不可能发生的事件具有更高的信息量。
- 独立事件应具有增量的信息。例如,投掷的硬币两次正面朝上传递的信息量,应该是投掷一次硬币正面朝上的信息量的两倍。
根据以上三点,定义自信息(self-information):
在本文中,用log来表示自然对数,其底数为e。
香农熵
设 X 是一个有限个值的离散随机变量,其概率分布为:
对于该离散随机变量,用自信息的期望来量化整个概率分布中的不确定性总量:
这里的H(X)定义为随机变量 X 的香农熵(Shannon entropy),香农熵只依赖于 X 的分布,而与 X 的取值无关,所以香农熵也记作H(P)。
下面借助抛硬币的例子来简单理解一下香农熵。
在抛硬币时,假设正面朝上的概率为p,反面朝上的概率为1-p,即 P(X=正) = p, P(X=反) = 1-p,香农熵大小为:
H(p)随概率p变化的曲线为:
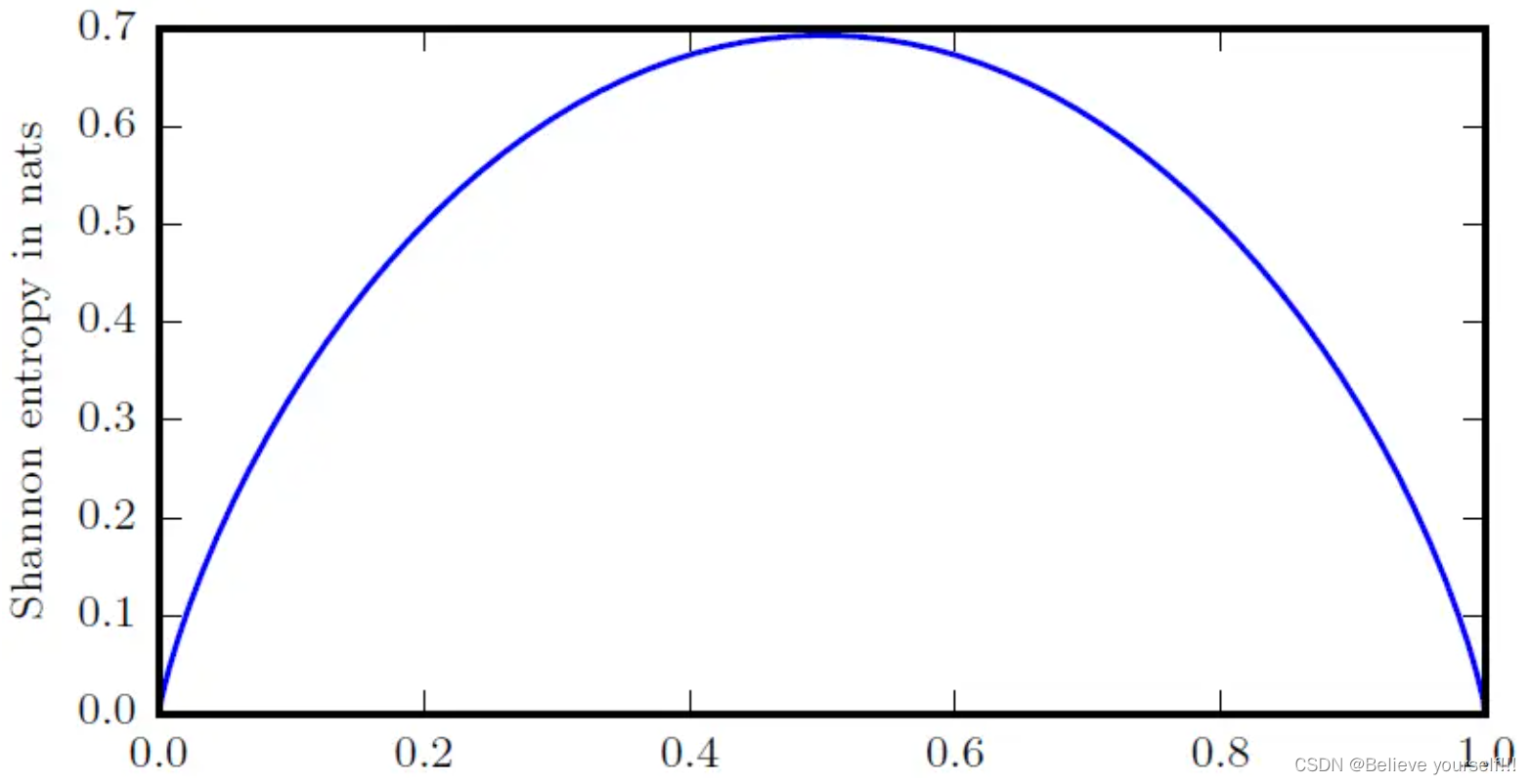
从上图中可以看到,当正面朝上的概率p=0或1时,这时我们完全可以确定抛硬币的结果,此时香农熵H(p)=0,随机变量完全没有不确定性。当p=0.5时,正面和反面出现的概率相同,我们完全无法确定结果,此时香农熵取值最大,随机变量不确定性也最大。这说明了更接近确定性的分布具有较低的香农熵,而更接近均匀分布的分布(不确定性最大)具有较高的香农熵。
KL散度(相对熵)
KL散度(Kullback-Leibler divergence),也叫做相对熵。若随变量 X 有两个单独的概率分布P(X)和Q(X),可以用相对熵来衡量这两个分布的差异,相对熵的定义如下:
相对熵是非负的(关于KL散度或者相对熵非负性的证明,可以参考我的另一篇文章:KL散度非负性证明),它的大小可以用来衡量两个分布之间的差异,当且仅当P和Q具有完全相同的分布时,相对熵取值为0。
交叉熵
通过上面的介绍,相信聪明的同学已经发现可以通过最小化相对熵来用分布Q逼近分布P(目标概率分布)。首先我们对相对熵公式进行变形:

这里的H(P,Q)就是交叉熵(cross-entropy),它的表达式为:
对于确定的概率分布P,它的香农熵H(P)是一个常数,所以要对相对熵 进行最小化,只需对交叉熵H(P,Q)做最小化处理即可。
通过最小化交叉熵,就可以得到分布P的近似分布,这也是为什么可以用交叉熵作为网络的损失函数。
交叉熵损失函数
交叉熵损失函数常用于分类问题中,下面以图像分类问题来举例说明。
为了计算网络的loss,模型的输出要确保归一化到0到1之间,二分类问题通常使用sigmoid函数来进行归一化,多分类问题通常使用softmax函数来归一化。
假设我们需要对数字1,2,3进行分类,它们的label依次为:
[1,0,0], [0,1,0], [0,0,1]
当输入的图像为数字1时,它的输出和label为:
[0.3,0.4,0.3] , [1,0,0]
接下来我们就可以利用交叉熵计算网络的
随着训练次数的增加,模型的参数得到优化,这时的输出变为:[0.8,0.1,0.1]
则
可以发现loss由1.20减小为0.22,而判断输入图像为数字1的概率由原本的0.3增加为0.8,说明训练得到的概率分布越来越接近真实的分布,这样就大大的提高了预测的准确性。
【个人理解】深度学习中,在进行分类任务的时候,训练集就是一堆图片加上每一张图片对应的标签,比如MNIST手写数字识别数据集就是一张灰度图片加上10个类别的one-hot标签,这个时候,最理想的分布就是:输入一张图片比如数字1,输出对应类别的one-hot即[0,1,0,0,0,0,0,0,0,0] 。而我们实际在网络训练过程中的分布是:输入一张图片比如数字1,输出对应类别的one-hot即[0,0.8,0,0,0,0,0,0,0.2,0] 。可以看到我们训练时候的实际分布和最理想的分布之间还是存在差别的,这个时候我们就希望网络训练的时候,输入一张图片比如数字1,输出对应类别的one-hot尽可能的接近[0,1,0,0,0,0,0,0,0,0],也就是说,我们希望训练时候的分布尽可能的接近最理想的分布。而这种评估两个分布之间差异即为KL散度,所以说,交叉熵损失函数的核心思想就是使网络训练的分布尽可能接近Ground Truth的分布。