JCR1区局部强化优化器(PRO)，原理详解，MATLAB代码免费获取

局部强化优化器（Partial Reinforcement Optimizer, PRO）代表了进化计算领域的一项创新突破，它是一种全新设计的进化优化算法。该算法的开发灵感来源于心理学中的进化学习和训练理念，特指为一个被称为局部强化效应（Partial Reinforcement Effect, PRE）的理论。该理论探讨了在面对不确定性条件下，如何通过间歇性的奖励机制来显著提升学习过程的效率与成果。PRO算法正是将这种心理学理论应用于算法设计之中，从而提高算法在多样化环境下的适应能力和寻优效率。该成果于2023年发表在计算机领域一区期刊Expert Systems with Applications上。

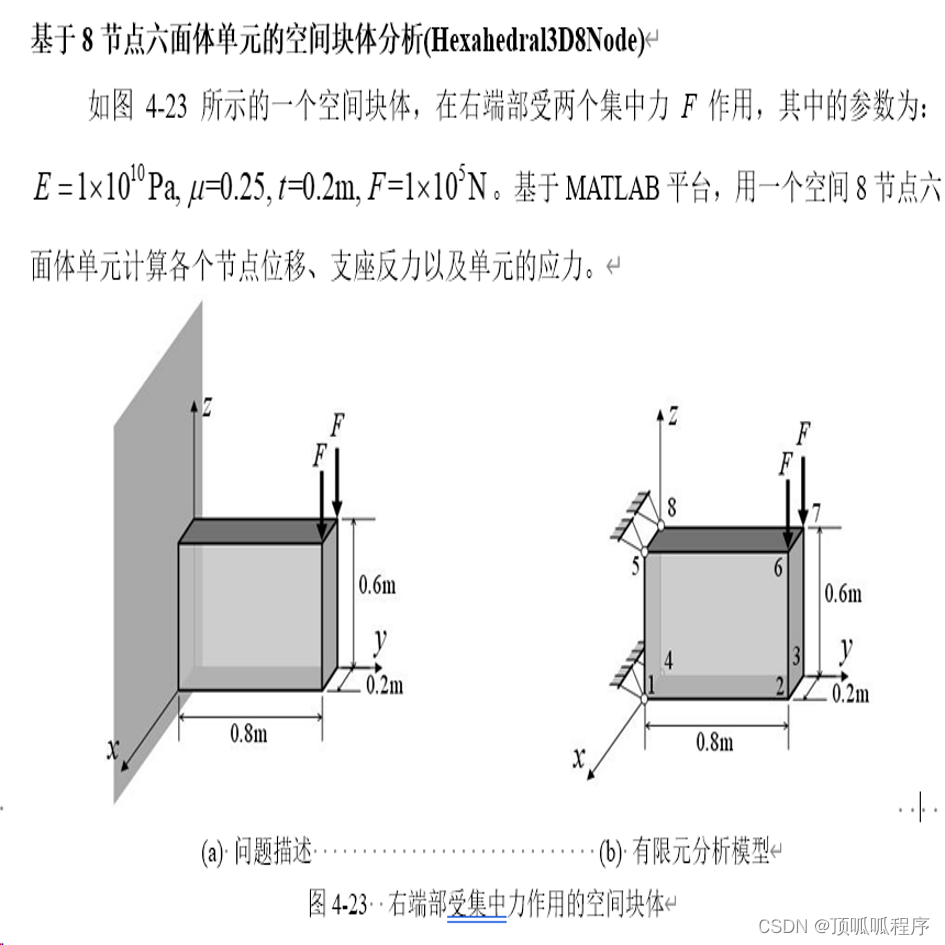
PRE理论基于心理学中的学习/训练范式，其中学习者间歇地而不是连续地得到强化，以提高他们的知识。强化的时机和频率对反应的速度和强度有显著影响。下图说明了PRE理论中正强化和负强化的一个例子。当狗（学习者）受到铃铛的刺激而传递球（反应）时，狗将得到积极的加强并传递球。或者，狗会得到负强化。

1、算法原理

为了将PRE理论的规则和概念映射到PRO算法的组件，有必要将PRE理论建模为优化算法。考虑了以下假设：

学习者：学习者是一个人或动物，其行为需要使用PRE理论进行训练/改进，并且它被建模为解决方案。

行为：学习者的行为被认为是一个决策变量解决方案。换句话说，解决方案(学习器)是决策变量(行为)的向量，如下图所示。

总体:在PRO算法中，一组学习者形成一个总体。下图中的每一行代表一个解(学习者)，每个元素Xdi代表一个决策变量(行为)。

适应度(目标函数)评估:使用用户定义的目标函数对决策变量计算每个学习者Xi的行为适应度。

时间(间隔):两个刺激、评估或强化阶段之间的迭代次数，它指定了学习者在搜索过程中的决策变量(行为)，被认为是一个时间间隔。在提出的算法中，使用了评分机制，因此得分较高的行为在下一次迭代中得到加强的机会更高。

回应:主要目标是获得更多的回应。在本研究中，响应被定义为目标函数值的成功改进。因此，F(X′)< F(X)，其中F(X′)和F(X)分别为刺激阶段结束后某一特定解的当前和先前目标函数值。

调度:调度的概念是指在不同的时间间隔内为数据结构建模时，需要如何以及何时加强行为。如下图所示，每个学习者都有一个特定的时间表。由于每个标量代表了特定学习者行为的分数/优先级，分数/优先级越高，下一次迭代中被选择的机会就越大。此外，将变间隔调度方案建模为动态机制，利用以下方程进行随机分析。

式中，tau为时间因子，FEs为函数评价的次数，MaxFEs为函数评价的最大次数。其中，SR是选择率，是基于调度选择的行为子集， λ是选择子集的大小，是行为(决策变量)的总数。Schedule *表示排序优先级的Schedule, Schedule *，是Schedule *中的 λth项。

刺激:任何试图刺激学习者的行为以引起反应的尝试都是通过应用操作来改变所提出的解决方案的决策变量来建模的。需要注意的是，任何操作都可以用来刺激(改变)学习者的行为(决策变量)。在PRO算法中，使用以下操作来生成新的解，如下式所示。

式中，SFi为激励因子，为基于调度程序的第i个学习器所选择决策变量的归一化分数/优先级的平均值。

强化:为了概念化强化，我们使用以下机制来更新调度。然后应用正强化来增加特定行为的分数。学习者的目标函数作为刺激阶段改进后的响应，其数学表达式如下：

式中，RR为强化率， с表示第i个解(学习者)所选择的决策变量(行为)的优先级。

另一方面，当没有反应时，就会施加负强化。在这种情况下，学习者的目标函数在刺激阶段后减小，导致特定行为得分下降。在下一次迭代中选择得分较高的决策变量(行为)进行刺激和强化，如下式所示：

重新安排:这个概念指的是在训练期间为学习者应用新的计划的过程，当学习者的所有行为始终受到负强化时。在这种情况下，PRO利用计划的标准偏差(Std)作为度量来确定何时需要重新安排学习者的计划。这种机制是通过使用下式来实现。

式中，Std(Schedule)为第i个学习者的学习进度的标准差，LB和UB分别为下界和上界。U(0,1)和U(LB,UB)是指均匀分布在(0,1)和(LB,UB)之间的随机值。

PRO算法的伪代码如下图所示。

PRO算法的流程框图如下图所示

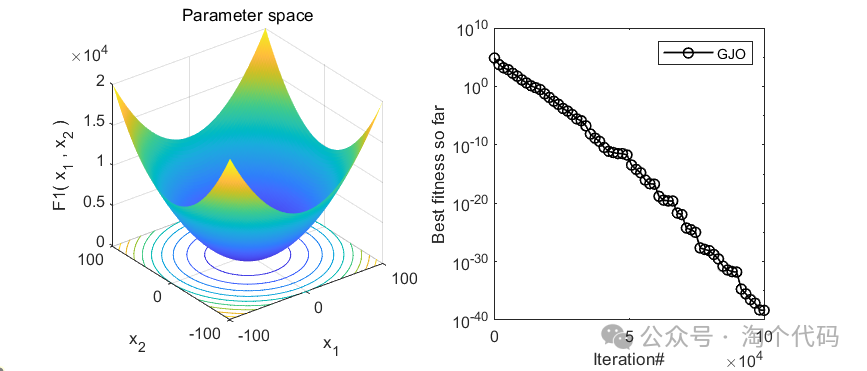
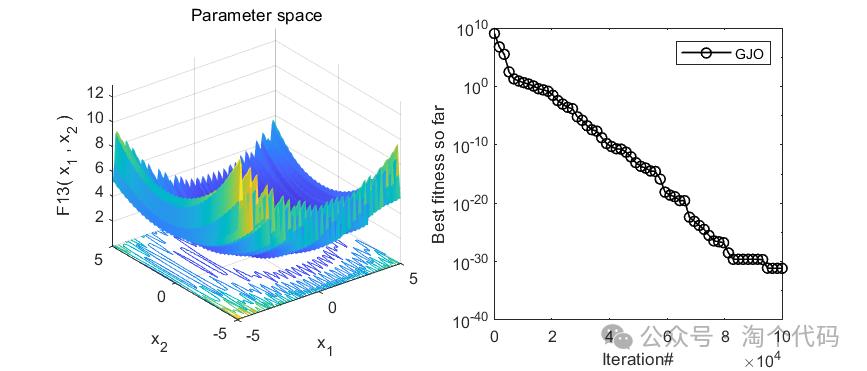
2、结果展示

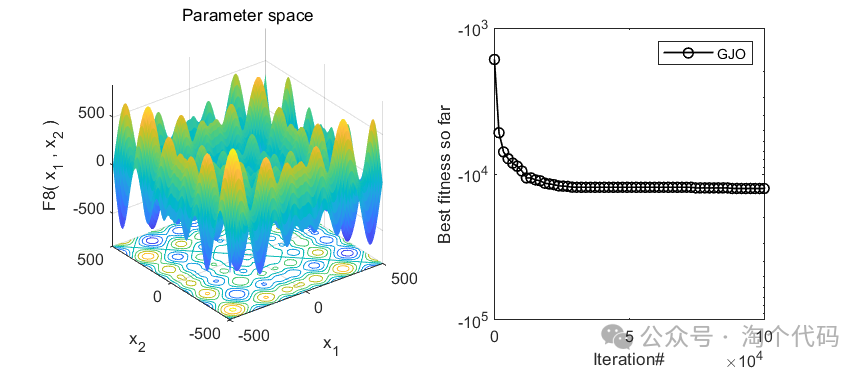
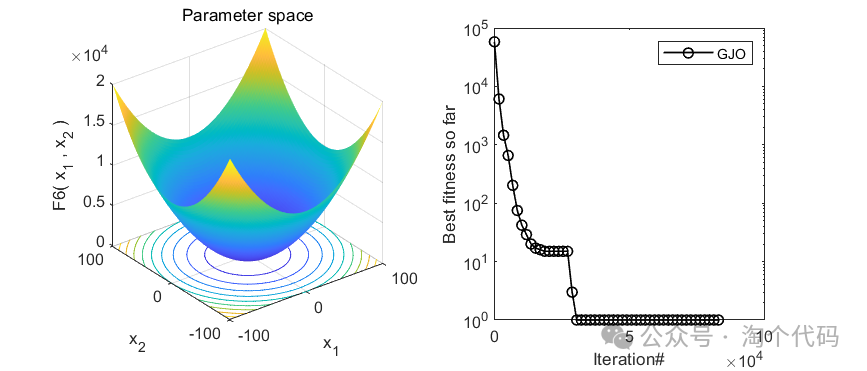
3、MATLAB核心代码

% 局部强化优化器（PRO）
Initialization 
rand('state',sum(100*clock));
% --- Problem Definition ---
%Obj_Func = @ YourObjFunc;         %  Objective Function
fhd = str2func('cec17_func');
nVar = N;                          %  Number of Decision Variables
%LB =  LB .* ones(1,nVar);          %  Variables Lower Bound
%UB =  UB .* ones(1,nVar);          %  Variables Upper Bound
% --- PRO Parameters ---
RR = 0.7;                          %  Reinforcement Rate (RR)
%MaxFEs = MaxFEs;                  %  Maximum Number of Function Evaluations
nPop = pop_size;                   %  Population Size
FEs = 0;                           %  Function Evaluations counter
% --- Empty Structure for Individuals ---
empty_individual.Behaviors=[];
empty_individual.response=[];
empty_individual.Schedule=[];
%empty_individual.Fy=[];
%empty_individual.Gx=[];
% --- Initialize Population Array ---
pop = repmat(empty_individual, nPop, 1);
% --- Initialize Best Solution ---
BestSol.response = inf;
% --- Initialize Population --- 
for i=1:nPop
    pop(i).Behaviors = population(i).Position;
    pop(i).Schedule = unifrnd(0.9,1,1,N);
    pop(i).response =  population(i).Cost; %feval('cec14_func',pop(i).Behaviors',CostFunction)  - (CostFunction*100);
end
% --- Sort pop ---
[~,SorteIndx] = sort([pop.response]);
pop = pop(SorteIndx);
% --- Set the Best Solution ---
BestSol = pop(1);
% --- Initialize Best Cost Record ---
BestCosts = zeros(MaxFEs,1);
BestCosts(1) = BestSol.response;
[~, sortedIndx] = sort([pop.response]);
ResetZero = zeros(1,N);
%% --- PRO Main Loop ---
 while FEs < MaxFEs 
    for i=1:nPop  % For all Learners      
       tempBehav = pop(i);% empty_individual;      
       k = nPop;
       if i < nPop
         k = sortedIndx(randi([i+1 nPop]));
       end    
       %% --- Determine Behaviors of the ith learner based on Scheduler. -----------  
       % According to Eq.(1) & Eq.(2)
       Tau = (FEs/MaxFEs);                          %  Time parameter
       %Selection_rate = Tau^0.5; 
       Selection_rate = exp(-(1-Tau)); %******** 
       %Selection_rate = exp(-(Tau))^2;
       [~,Candid_Behavs] = sort(pop(i).Schedule(1:N),'descend');
       % --Select Landa number of Behaviors with highest priority in Schedule i.-- 
       Landa = ceil(N*rand*Selection_rate);
       Selected_behaviors = Candid_Behavs(1:Landa);%
       %% --- Stimulate the selected Behaviors of the ith learner to get response.---  
       % According to Eq.(3), Eq.(4), and Eq.(5)
       if rand <  0.5 %(0.1 + 0.9 * (1-Tau))
          Stimulation = ResetZero;
          Stimulation(Selected_behaviors) = ( BestSol.Behaviors(Selected_behaviors) - pop(i).Behaviors(Selected_behaviors));    
       else
          Stimulation = ResetZero;
          Stimulation(Selected_behaviors) = ( pop(i).Behaviors(Selected_behaviors) - pop(k).Behaviors(Selected_behaviors));            
       end
       % ---- Calculate Stimulation Factor (SF) ------
       %SF = rand * ( exp(-1 * mean( abs(BestSol.Behaviors - pop(i).Behaviors)/max(abs(pop(1).Behaviors - pop(nPop).Behaviors)))));
       %SF = rand * ( exp(-1 * mean( abs(BestSol.Behaviors(Selected_behaviors) - pop(i).Schedule(Selected_behaviors))/max(abs(pop(i).Schedule(Selected_behaviors) - pop(nPop).Schedule(Selected_behaviors))))));
       SF = Tau + rand * (mean((pop(i).Schedule(Selected_behaviors) )/max(abs(pop(i).Schedule)))); %(exp(-(1-FEs/MaxFEs))^2 ) ;
       tempBehav.Behaviors(Selected_behaviors) = pop(i).Behaviors(Selected_behaviors) + SF .* Stimulation(Selected_behaviors);    
       % ------------  Bound constraints control ------------------- 
       % 
       [~,underLB] = find(tempBehav.Behaviors < LB);
       [~,uperUB] = find(tempBehav.Behaviors > UB);
       if ~isempty(underLB)
         tempBehav.Behaviors(underLB) =  LB(underLB) + rand(1,size(underLB,2)).*((UB(underLB) -  LB(underLB))./1); 
       end
       if ~isempty(uperUB)
         tempBehav.Behaviors(uperUB) =  LB(uperUB) + rand(1,size(uperUB,2)).*((UB(uperUB) -  LB(uperUB))./1); 
       end
       % ------ Evaluate the ith learner Response -------------------
       %tempBehav.response = feval('cec14_func',tempBehav.Behaviors',ObjFunc_ID)  - (ObjFunc_ID*100);
       %tempBehav.response = feval(fhd,tempBehav.Behaviors',ObjFunc_ID); %CEC2017
       tempBehav.response = Sphere(tempBehav.Behaviors'); % Test Func
       FEs = FEs + 1;
       % ----- Apply Positive or Negative Reinforcement according to the response.
       % According to  Eq.(6)& Eq.(7)
       if tempBehav.response<pop(i).response
            % Positive Reinforcement 
            tempBehav.Schedule(Selected_behaviors) = pop(i).Schedule(Selected_behaviors) + pop(i).Schedule(Selected_behaviors) * (RR/2);           
            % accept new Solution
            pop(i) = tempBehav;
            % Update the best Solution
            if pop(i).response < BestSol.response
                BestSol = pop(i);  
            end
       else
               % Negative Reinforcement
               pop(i).Schedule(Selected_behaviors) = pop(i).Schedule(Selected_behaviors) - pop(i).Schedule(Selected_behaviors) * (RR);
       end
       % Store Record for Current Iteration
       BestCosts(FEs) = BestSol.response; 
       %% ------- Rescheduling --------------------------------------------------    
       if std(pop(i).Schedule(1:N))== 0
           pop(i).Schedule = unifrnd(0.9,1,1,N);
           pop(i).Behaviors = LB+rand(1,N).*(UB-LB);
           %pop(i).response = feval('cec14_func',pop(i).Behaviors',ObjFunc_ID)  - (ObjFunc_ID*100);
           %pop(i).response = feval(fhd,pop(i).Behaviors',ObjFunc_ID); %CEC2017
           pop(i).response = Sphere(pop(i).Behaviors'); % Test Func
           disp(['-------------------------------- The  Learner ' num2str(i) ' is Rescheduled ']);
       end
   end % End for nPop
   %% Sort pop
   [~,SorteIndx] = sort([pop.response]);
   pop = pop(SorteIndx);
   % --- Show Iteration Information ---
   disp(['Iteration ' num2str(FEs) ': Best Cost = ' num2str(BestCosts(FEs))  ]);
 end % End While
BestSolCost=BestSol.response
end % Function PRO_v1()

参考文献

[1]Taheri A, RahimiZadeh K, Beheshti A, et al. Partial reinforcement optimizer: An evolutionary optimization algorithm[J]. Expert Systems with Applications, 2024, 238: 122070.

完整代码获取

后台回复关键词：

TGDM899