今日任务
- 20 有效的括号 (题目: . - 力扣(LeetCode))
- 1047 删除字符串中的所有相邻重复项 (题目: . - 力扣(LeetCode))
- 150 逆波兰表达式求值 (题目: . - 力扣(LeetCode))
20 有效的括号
题目: . - 力扣(LeetCode)
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
想法:
非常经典的一道题, 在大学课堂上老师就讲过这道题, 对栈的理解及应用, 思路比较清晰,题意其实就像我们在写代码的过程中,要求括号的顺序是一样的,有左括号,相应的位置必须要有右括号。
问题:
有思路,手生,代码写错了一坨🤣、还有就是未习惯用基础数据类型如何模拟其他数据结构, 愣是没想着用切片模拟栈的基础行为; 还停留在我要不要先实现个栈,再操作.
解决思路:
Go 语言,定义一个切片来当做栈.
(1)遍历字符串, 遇到左括号就加入栈
(2)遇到右括号,就判断是否和栈顶元素匹配,不匹配的话,直接 return false.因为当前的右括号必须和前一个匹配. 匹配之后,记得将栈顶元素弹出,进入下一个 for 循环.
(3) 若字符串遍历完, 栈中还有元素,false;
// 用切片模拟栈,来实现,就是碰到是左括号的就入栈、
// 碰到右括号,栈为空或者栈顶元素不是相匹配的就 return false.
// 匹配的话,就将栈顶元素移除,然后 for 循环也进入下一步.
// 如果 for 循环完了,栈还有数据,也要 return false
func isValid(s string) bool{
// m 用来记录左右括号的匹配关系
m := make(map[rune]rune)
m[')'] = '('
m['}'] = '{'
m[']'] = '['
stack := make([]rune,0)
for _,v := range s{
if v == '(' || v == '{' || v == '[' {
// 左括号压入栈
stack = append(stack,v)
} else {
// 右括号时,若栈内无匹配元素,则 false
if len(stack) == 0 {
return false
}
if stack[len(stack)-1] != m[v] {
return false
}
// 模拟弹出栈顶元素
stack = stack[0:len(stack)-1]
}
}
if len(stack) != 0{
return false
}
return true
}1047 删除字符串中的所有相邻重复项
题目:. - 力扣(LeetCode)
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。在 S 上反复执行重复项删除操作,直到无法继续删除。

想法:
和上题 有效的括号一样, 甚至更简单了, 只要当前元素和栈顶元素相等,将栈顶元素弹出就可以下一循环
问题:
无问题,easy
解决思路:
Go 语言,定义一个切片来当做栈.
(1)遍历字符串, 若栈未空,将当前元素加入栈. 栈不空,则对比栈顶元素是否相等,相等就将栈顶元素弹出.
(3) 若字符串遍历完, 将栈内元素拼接转为字符串即可.
func removeDuplicates(s string) string {
stack := make([]rune, 0)
for _, v := range s {
// 如果栈里没有元素,就将当前元素压入栈
if len(stack) == 0 {
stack = append(stack, v)
continue
}
// 如果当前元素与栈顶相同,就将栈顶元素移除
if stack[len(stack)-1] == v {
stack = stack[0 : len(stack)-1]
continue
}
// 否则就将元素压栈
stack = append(stack, v)
}
return string(stack)
}150 逆波兰表达式求值
题目: . - 力扣(LeetCode)
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如
( 1 + 2 ) * ( 3 + 4 )。 - 该算式的逆波兰表达式写法为
( ( 1 2 + ) ( 3 4 + ) * )。
逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成
1 2 + 3 4 + *也可以依据次序计算出正确结果。 - 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
想法:
一开始看题目有点没太理解, 看到了逆波兰表达式的解释,也能想到会用栈,但是我的想法错误. 我一直盯着最后面的字符串往前看,想取到最后一个字符,我要往前找两个数字字符.去进行运算.
问题:
上面标红线的思路理解后,代码也是非常简单, 最大的困难可能看到那么多数字和 运算符号混在一起容易吓到. 不知道该如何处理了
解决思路:
有张图挺好的, 看一眼就能直接理解了,参考自: 代码随想录
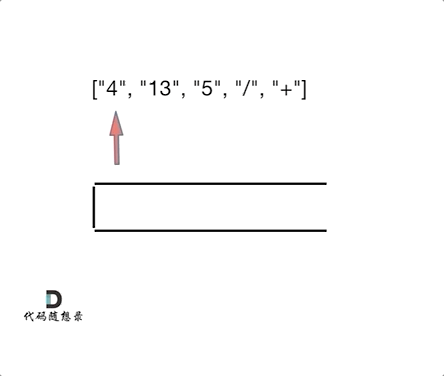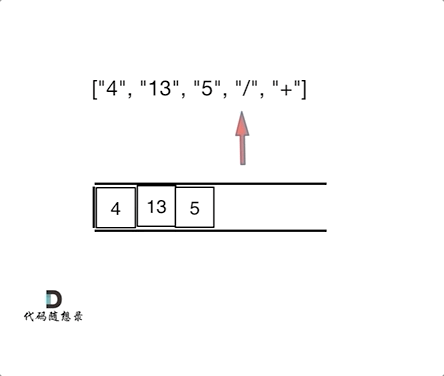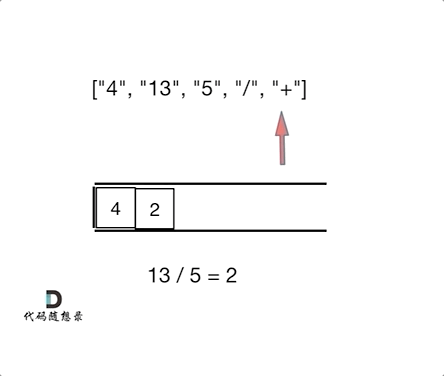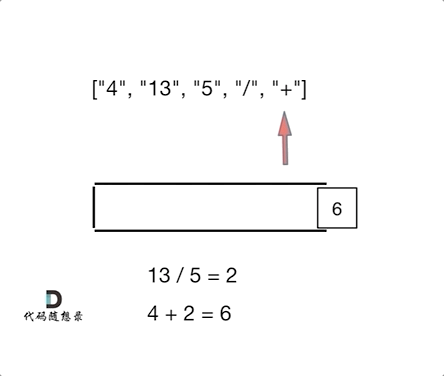
我们习惯看到的表达式都是中缀表达式,因为符合我们的习惯,但是中缀表达式对于计算机来说就不是很友好了。
例如:4 + 13 / 5,这就是中缀表达式,计算机从左到右去扫描的话,扫到13,还要判断13后面是什么运算符,还要比较一下优先级,然后13还和后面的5做运算,做完运算之后,还要向前回退到 4 的位置,继续做加法,你说麻不麻烦!
那么将中缀表达式,转化为后缀表达式之后:["4", "13", "5", "/", "+"] ,就不一样了,计算机可以利用栈来顺序处理,不需要考虑优先级了。也不用回退了, 所以后缀表达式对计算机来说是非常友好的。
func evalRPN(tokens []string) int {
stack := []int{}
for _, token := range tokens {
val, err := strconv.Atoi(token)
// 如果没报错,说明是数字
if err == nil {
stack = append(stack, val)
} else {
// 如果err不为nil说明不是数字
// 取栈顶的前两个元素 等会做运算,并将其从栈中弹出
num1, num2 := stack[len(stack)-2], stack[(len(stack))-1]
stack = stack[:len(stack)-2]
switch token {
case "+":
stack = append(stack, num1+num2)
case "-":
stack = append(stack, num1-num2)
case "*":
stack = append(stack, num1*num2)
case "/":
stack = append(stack, num1/num2)
}
}
}
return stack[0]
}