回溯算法
回溯法的作用
递归函数与回溯算法是相辅相成的,回溯法往往在递归函数的“下面”
使用原因:有些问题无法暴力进行搜索,只能通过回溯法来解决,例如
1.组合问题
2.切割问题
3.子集问题
4.排列问题
5.棋盘问题
回溯算法是一种效率很低的算法
理解回溯法
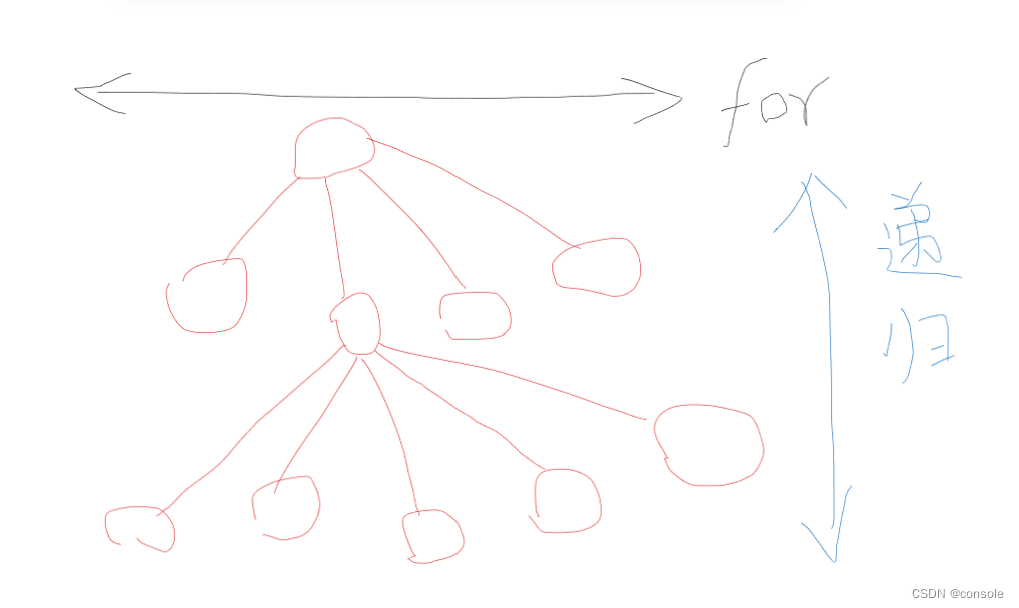
所有的回溯法都可以抽象为一个树形结构,因为回溯其实就是一个递归的过程,递归一定是有终止的,回溯法都可以抽象为一颗n叉树,树的宽度就是我们回溯法处理的集合的大小,通常使用for循环来遍历,树的深度就是递归的深度,因为递归一定是有终止的,终止之后会一层一层的向上返回,如下图所示
回溯法的模版
一般来说递归函数没有返回值,因此都是void,一般名为backtracking,回溯法的参数一般较多,在实现过程中需要用到数据再进行参数的添加,即为
void backtracking(参数列表)
{
//一般到达终止条件时,都是搜集结果的时候
if(终止条件)
{
收集结果
return ;
}
//单层搜索逻辑
for(集合的元素集)
{
处理节点;
递归函数;
回溯操作;//撤销处理节点的情况
}
return;
}
77.组合
链接:. - 力扣(LeetCode)
题目描述:
给定两个整数
n和k,返回范围[1, n]中所有可能的k个数的组合。你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]示例 2:
输入:n = 1, k = 1 输出:[[1]]提示:
1 <= n <= 201 <= k <= n
思路:
只能使用回溯算法来解决,回溯算法通过递归来控制for循环的层数,我们将其抽象为树形结构,我们以n为4,k为2为例,即如下图所示
在第一个子树里,我们将1取出来,再将2,3,4分别取出,就得到了我们需要的集合(叶子节点),从组合来看,12与21是一个集合,因此前面取出的元素不需要再放回去
回溯实现:
1.先确定递归函数的参数和返回值,返回值一般为空,我们需要n和k的值,使用一个变量,将我们每次递归开始要搜索的位置传递进来
2.确定递归终止条件,到了叶子节点就是我们需要的结果,就进行结果的收集
3.确定单层递归逻辑,每一个节点都是一个for循环,起始位置都是开始要搜索的位置传递进来,遍历剩余的元素,存放路径,再去递归遍历,再进行回溯的过程
代码实现:
/** * Return an array of arrays of size *returnSize. * The sizes of the arrays are returned as *returnColumnSizes array. * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free(). */ //用来存储单个集合的结果 int *path; //用来记录单个集合里的元素个数 int pathtop; //存储全部的结果 int **ans; //记录最后得到的组合数 int anstop; void backtracking(int n, int k, int startindex) { //当单个结果集的元素个数满足我们k值时 if(pathtop == k) { //由于 backtracking 函数中 path 数组是在递归过程中不断修改的,如果直接将 path 数组的地址存储到 ans 数组中,那么最终 ans 中的所有结果集都将指向同一个地址,导致结果错误 int *tem = (int *)malloc(sizeof(int) * k); for(int i = 0; i < k; i++) { tem[i] = path[i]; } //将单个结果集存入全部的数组中 ans[anstop++] = tem; return ; } int j; //每次开始遍历的位置 for(j = startindex; j <= n; j++) { //记录遍历过的值 path[pathtop++] = j; //递归遍历剩余的元素,从当前的下一个开始 backtracking(n,k,j+1); //回溯到上一步 --pathtop; } } int** combine(int n, int k, int* returnSize, int** returnColumnSizes) { // 分配存储结果的指针数组空间 ans = (int **)malloc(sizeof(int *) * 1000); // 分配存储当前组合的数组空间 path = (int *)malloc(sizeof(int) * k); // 初始化结果数组和当前组合数组的索引 anstop = pathtop = 0; backtracking(n,k,1); // 将结果集中的组合的个数存储 *returnSize = anstop; // 分配存储每个组合长度的数组空间 *returnColumnSizes = (int*)malloc(sizeof(int) * (*returnSize)); for(int i = 0; i < *returnSize; i++) { (*returnColumnSizes)[i] = k; } return ans; }
根据我们抽象出来的树形结构,我们其实可以看出有些部分的遍历其实是无用的,因为元素个数的组合已经不可能到达k个,因我们可以进行剪枝的操作,这样我们就可以减少遍历的次数
在回溯函数中的for循环里,我们每次都会从开始位置遍历到n的位置,其中有很多的步骤是不必要的,因为我们需要得到的每个子集的元素个数为k,而我们已经拿到了pathtop个元素,因此我们还需要的元素个数就应该为k-pathtop
因此我们在集合n中最多从n-(k-pathtop)+1的位置开始遍历,再往后遍历即使加上我们前面的已经取到的元素,也达不到k个,因此就不需要再往后进行遍历
在这里
n是集合中的总元素数量。
k - pathtop是还需要选择的元素数量。因此,
n - (k - pathtop)表示从集合中剩余的元素中开始选择。加上
1是因为在程序中,数组的索引是从0开始的,而不是从1开始的。因此,我们需要考虑起始位置的下一个位置作为实际的起始索引,以确保包含了剩余的元素。综上所述,加上
1是为了正确计算起始位置的索引,确保我们在遍历时能够包括剩余的元素根据分析,就可以知道剪枝后的代码只需要修改for循环中的条件部分
void backtracking(int n, int k, int startindex) { //当单个结果集的元素个数满足我们k值时 if(pathtop == k) { //由于 backtracking 函数中 path 数组是在递归过程中不断修改的,如果直接将 path 数组的地址存储到 ans 数组中,那么最终 ans 中的所有结果集都将指向同一个地址,导致结果错误 int *tem = (int *)malloc(sizeof(int) * k); for(int i = 0; i < k; i++) { tem[i] = path[i]; } //将单个结果集存入全部的数组中 ans[anstop++] = tem; return ; } int j; //每次开始遍历的位置 for(j = startindex; j <= n - (k-pathtop) + 1; j++) { //记录遍历过的值 path[pathtop++] = j; //递归遍历剩余的元素,从当前的下一个开始 backtracking(n,k,j+1); //回溯到上一步 --pathtop; } }