一、参考资料
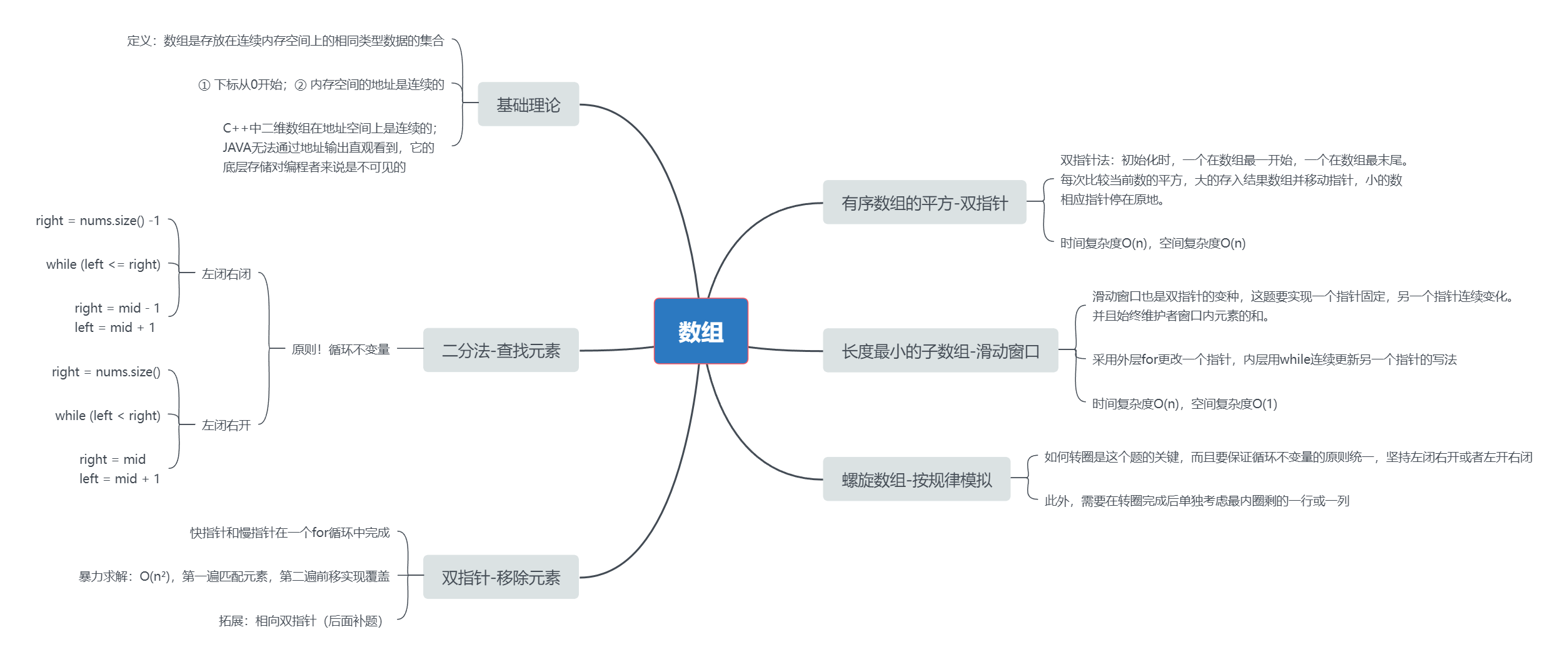
有序数组的平方
题目链接:https://leetcode.cn/problems/squares-of-a-sorted-array/
文章讲解:https://programmercarl.com/0977.%E6%9C%89%E5%BA%8F%E6%95%B0%E7%BB%84%E7%9A%84%E5%B9%B3%E6%96%B9.html
视频讲解: https://www.bilibili.com/video/BV1QB4y1D7ep
长度最小的子数组
题目链接:https://leetcode.cn/problems/minimum-size-subarray-sum/
文章讲解:https://programmercarl.com/0209.%E9%95%BF%E5%BA%A6%E6%9C%80%E5%B0%8F%E7%9A%84%E5%AD%90%E6%95%B0%E7%BB%84.html
视频讲解:https://www.bilibili.com/video/BV1tZ4y1q7XE
螺旋矩阵II
题目链接:https://leetcode.cn/problems/spiral-matrix-ii/
文章讲解:https://programmercarl.com/0059.%E8%9E%BA%E6%97%8B%E7%9F%A9%E9%98%B5II.html
视频讲解:https://www.bilibili.com/video/BV1SL4y1N7mV/
数组专题总结
文章链接:https://programmercarl.com/%E6%95%B0%E7%BB%84%E6%80%BB%E7%BB%93%E7%AF%87.html
二、LeetCode977-有序数组的平方
我的代码(过于暴力)
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
vector<int> res;
for (int i = 0; i < nums.size(); i++){
nums[i] = nums[i] * nums[i];
}
sort(nums.begin(), nums.end());
return nums;
}
};接下来学习一下双指针的代码实现:
双指针实现
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
// 这里定义一个结果集,长度为原数组的大小
vector<int> res(nums.size(), 0);
// 定义首尾指针
int firstp = 0;
int lastp = nums.size() - 1;
int k = lastp; // k表示结果集的指针,从后向前写入vector
while (firstp <= lastp){
if (nums[firstp] * nums[firstp] < nums[lastp] * nums[lastp]){
res[k--] = nums[lastp] * nums[lastp];
lastp--;
}
else{
res[k--] = nums[firstp] * nums[firstp];
firstp++;
}
}
return res;
}
};三、LeetCode209-长度最小的子数组
最大的收获是学习了滑动窗口的写法!视频讲解很详细
滑动窗口-代码实现
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int result = INT32_MAX;
int sum = 0;
// 滑动窗口的起始位置
int begin = 0;
// 滑动窗口的长度
int subLen = 0;
for (int i = 0; i < nums.size(); i++){
sum += nums[i];
while (sum >= target){
subLen = (i - begin + 1);
result = result < subLen ? result : subLen;
sum -= nums[begin];
begin++;
}
}
if (result == INT32_MAX){
return 0;
}
return result;
}
};问题:
INT32_MAX是什么?它表示数组中一个很大的数,进一步,它是在limits.h下面的一个宏。
https://blog.csdn.net/wangshuqian1314/article/details/122657716
卡哥讲解!
滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。
时间复杂度O(n),空间复杂度O(1)
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int result = INT32_MAX;
int sum = 0; // 滑动窗口数值之和
int i = 0; // 滑动窗口起始位置
int subLength = 0; // 滑动窗口的长度
for (int j = 0; j < nums.size(); j++) {
sum += nums[j];
// 注意这里使用while,每次更新 i(起始位置),并不断比较子序列是否符合条件
while (sum >= s) {
subLength = (j - i + 1); // 取子序列的长度
result = result < subLength ? result : subLength;
sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处,不断变更i(子序列的起始位置)
}
}
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == INT32_MAX ? 0 : result;
}
};四、LeetCode59-螺旋矩阵II
这个题以前是做过的,先用学会的模拟实现一下
我的代码(数组模拟)
class Solution {
public:
// 这题之前也写过,但还是不太熟练呐
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n)); // 初始化二维数组
// 定义上下左右四个方向的索引
int t = 0; // top
int b = n - 1; // bottom
int l = 0; // left
int r = n - 1; // right
// 螺旋矩阵的计数(即填入矩阵的数值)
int k = 1;
while (k <= n * n){
for(int i = l; i <= r; i++, k++){
res[t][i] = k;
}
t++;
for(int i = t; i <= b; i++, k++){
res[i][r] = k;
}
r--;
for(int i = r; i >= l; i--, k++){
res[b][i] = k;
}
b--;
for(int i = b; i >= t; i--, k++){
res[i][l] = k;
}
l++;
}
return res;
}
};卡哥讲解!
求解本题依然是要坚持循环不变量原则【处理的原则:统一的左闭右开】
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定义一个二维数组
int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
int loop = n / 2; // 每个圈循环几次,例如n为奇数3,那么loop = 1 只是循环一圈,矩阵中间的值需要单独处理
int mid = n / 2; // 矩阵中间的位置,例如:n为3, 中间的位置就是(1,1),n为5,中间位置为(2, 2)
int count = 1; // 用来给矩阵中每一个空格赋值
int offset = 1; // 需要控制每一条边遍历的长度,每次循环右边界收缩一位
int i,j;
while (loop --) {
i = startx;
j = starty;
// 下面开始的四个for就是模拟转了一圈
// 模拟填充上行从左到右(左闭右开)
for (j = starty; j < n - offset; j++) {
res[startx][j] = count++;
}
// 模拟填充右列从上到下(左闭右开)
for (i = startx; i < n - offset; i++) {
res[i][j] = count++;
}
// 模拟填充下行从右到左(左闭右开)
for (; j > starty; j--) {
res[i][j] = count++;
}
// 模拟填充左列从下到上(左闭右开)
for (; i > startx; i--) {
res[i][j] = count++;
}
// 第二圈开始的时候,起始位置要各自加1, 例如:第一圈起始位置是(0, 0),第二圈起始位置是(1, 1)
startx++;
starty++;
// offset 控制每一圈里每一条边遍历的长度
offset += 1;
}
// 如果n为奇数的话,需要单独给矩阵最中间的位置赋值
if (n % 2) {
res[mid][mid] = count;
}
return res;
}
};Day02总结:
最大的收获是学习了滑动窗口,写代码的熟练度还需要加强
数组模拟注意边界问题,主要是想明白怎么轮转的,将清楚的逻辑转化为代码实现
双指针还需要多多练习,多看题目和多思考~
五、数组专题总结