上节内容回顾：

• Vectors
  • Basic operations: addition, multiplication
• Dot Product
  • Forward / backward ( dot product positive / negative )
• Cross Product
  • Left / right ( cross product outward / inward )
• Matrics

本节知识概要

• Transformation!
• Today
  • Why study transformation
  • 2D transformations: rotation, scale, shear
  • Homogeneous coordinates
  • Composing transforms
  • 3D transformations

Why study transformation

Modeling 模型变换

rotation 旋转
scaling 缩放
…

Viewing 视图变换

projection 投影
…

2D transformations 二维变换

• Representing transformation using matrices
• Rotation, scale, shear

Scale

Uniform 均匀缩放

$$\begin{gathered} x^{\prime }=sx \\ {y}^{\prime }=sy \end{gathered}$$
写成矩阵乘法：
$$\left[\begin{array}{c}x’\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}s& 0\\ 0& s\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

Non-Uniform 非均匀缩放

$$\begin{gathered} x^{\prime }=s_x\cdot x \\ {y}^{\prime }=s_y\cdot y \end{gathered}$$
写成矩阵乘法：
$$\left[\begin{array}{c}x’\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}{s}_x& 0\\ 0& s_y\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

Reflection Matrix 反射矩阵

水平反射

$$\begin{gathered} x^{\prime }=-x \\ {y}^{\prime }=y \end{gathered}$$

写成矩阵乘法：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

shear 切变

写成矩阵乘法：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}1& a\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

rotate 旋转，默认绕（0,0）旋转，默认逆时针方向

rotation matrix 旋转矩阵

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

Linear Transformation = Matrix

$$\begin{gathered} x^{\prime }=ax+by \\ {y}^{\prime }=cx+dy \end{gathered}$$

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

$$x^{\prime }=Mx$$

Homogeneous coordinates 齐次坐标

Translation 平移

平移变换很特殊

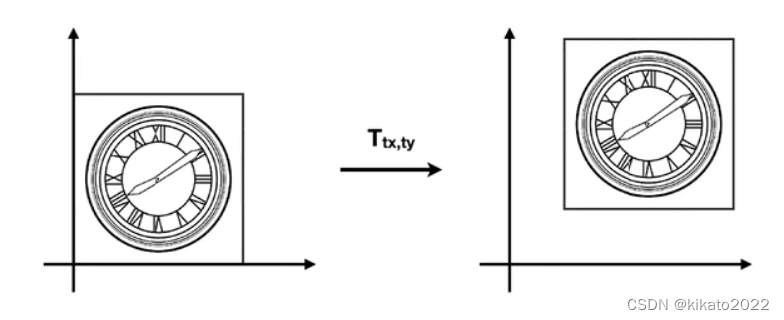
平移变换无法用矩阵乘法表示

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right]$$

但是我们并不希望平移变换独立开来，我们希望把平移变换也统一到矩阵乘法里面。
解决办法：齐次坐标(Homogenous coordinates)

其次坐标添加第三个坐标

若表示二维的点: 用（x，y，1）
若表示二维的向量：用（x，y，0）
注：因为向量具有平移不变性，所以向量的w坐标是0.
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ w^{\prime }\end{array}\right]=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]+\left[\begin{array}{c}x+t_x\\ y+t_y\\ 1\end{array}\right]$$

而且齐次坐标还满足：
向量 + 向量 = 向量
点 - 点 = 向量
点 + 向量 = 点
点 + 点 = ？？

要得到问号的答案，需要用到齐次坐标的扩充定义：
$$\left[\begin{array}{c}x\\ y\\ w\end{array}\right]isthe2Dpoint\left[\begin{array}{c}x/w\\ y/w\\ 1\end{array}\right],w\ne 0$$
所以 点+点 = 两点中点。

Affine Transformation

Affine map = linear map + translation

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right]$$

Using homogenous coordinates:

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}a& b& t_x\\ c& d& t_y\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

使用齐次坐标后的各种变换

Scale

$$S(s_x,s_y)=\left[\begin{array}{ccc}{s}_x& 0& 0\\ 0& s_y& 0\\ 0& 0& 1\end{array}\right]$$

Rotation

$$R(\alpha )=\left[\begin{array}{ccc}\cos \alpha & -\sin \alpha & 0\\ \sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]$$

Translation

$$T(t_x,t_y)=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]$$

Inverse Transform 逆变换

$$M^{-1}$$
$M^{-1}$ is th inverse of transform $M$ in both a matrix and geometic sense。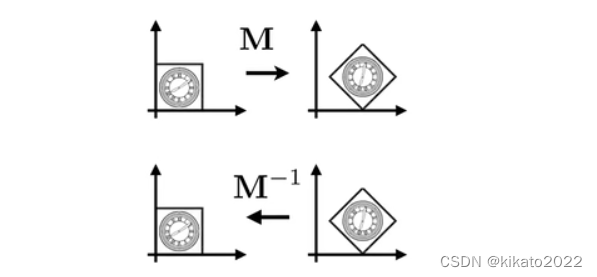

复杂的变换由简单的变换组合得到

注意：变换的顺序很重要
矩阵的乘法不满足交换律，所以先旋转再平移和先平移再旋转得到的结果是不一样的。

注意：连续矩阵相乘，是从右到左逐个应用的。

写完之后，可以把左边的矩阵先全部乘起来，得到的矩阵可以表示这个复杂的变换。

将复杂的变换先拆解

如何以c点为中心进行旋转？

1. 先平移到原点
2. 绕原点进行旋转
3. 再平移回去