java数据结构与算法刷题目录（剑指Offer、LeetCode、ACM）-----主目录-----持续更新(进不去说明我没写完)：https://blog.csdn.net/grd_java/article/details/123063846

数学：阶乘的10因子个数

解题思路：时间复杂度O($n$)，n为5的个数，空间复杂度O($1$)

1. 如果想要求出阶乘，一定会超时。所以我们要找到破题点。就是什么条件下阶乘末尾会出现0。
2. 我们发现阶乘结果求出来后，不断的提出因子10，能提出多少次，就有几个0. 例如5！=120. 此时进行因式分解为：$10\ast (12).$一共提出1个10，因此一共一个0.
3. 10是由2和5构成的。而且5的个数绝对更少。例如120 = $5\ast (24)$ = $2\ast 2\ast 2\ast (15)$.我们发现5的个数决定了阶乘结果中可以和2组成几个10.
4. 因此我们可以先尝试统计n的阶乘中，5的个数。试一下效果

我们不需要每个阶乘数字都统计，例如5！中只有5这个数会出现5.因为5！=1*2*3*4*5.明眼人都知道，1,2,3,4不会有5的出现。

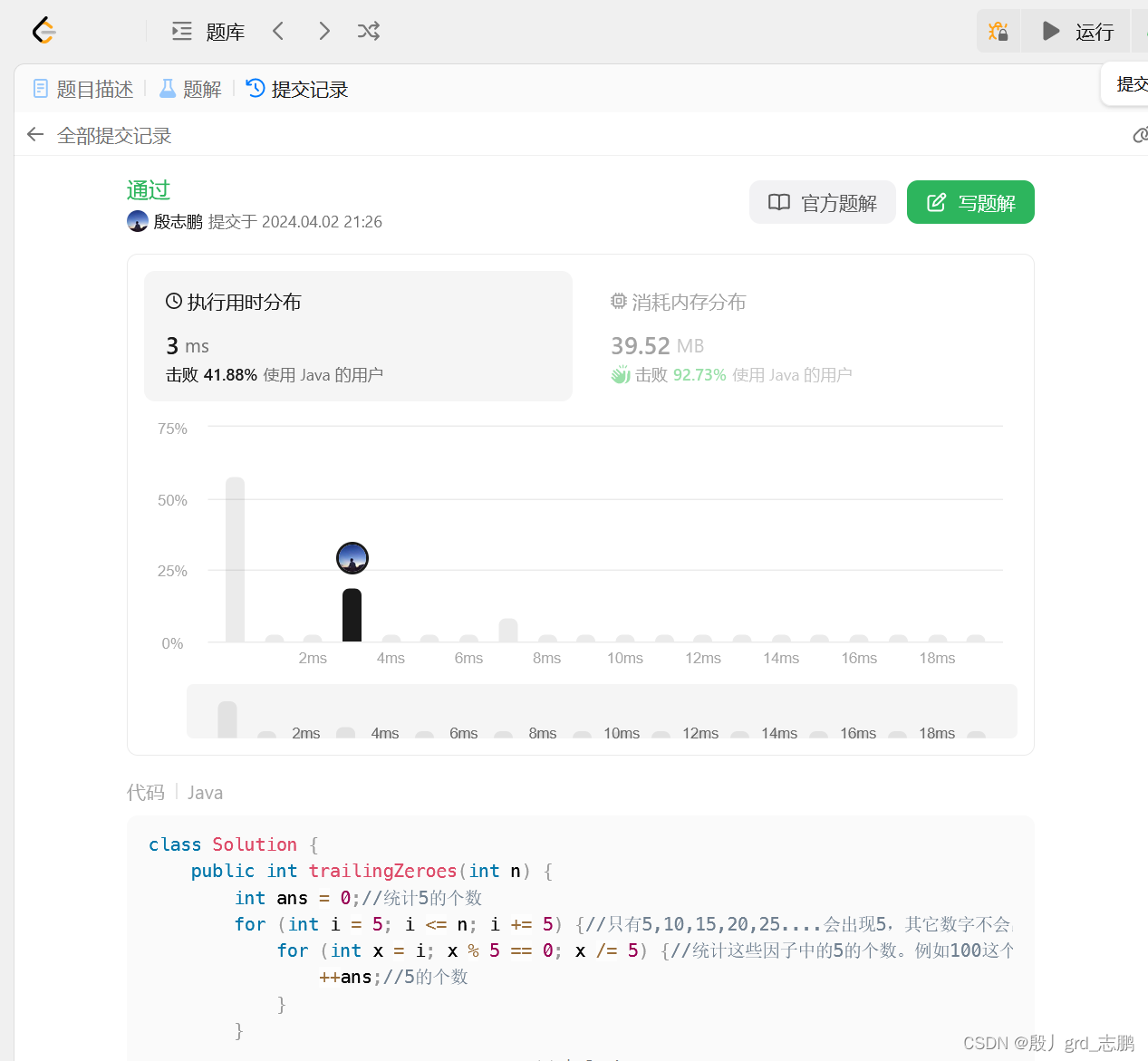
代码：最起码通过了对吗，说明想法没错，接下来法二会继续优化

class Solution {
    public int trailingZeroes(int n) {
        int ans = 0;//统计5的个数
        for (int i = 5; i <= n; i += 5) {//只有5,10,15,20,25....会出现5，其它数字不会出现5
            for (int x = i; x % 5 == 0; x /= 5) {//统计这些因子中的5的个数。例如100这个因子，可以拆解为5*5*4.有两个5
                ++ans;//5的个数
            }
        }
        return ans;
    }
}

数学优化:思路转变为求5的倍数的个数

解题思路：时间复杂度O($lo{g}_{2}n$)，空间复杂度O($1$)

1. 以1000为例：1000 = $5\ast 200$ = $5\ast 5\ast 40$ = $5\ast 5\ast 5\ast 8$ = $5\ast 5\ast 5\ast 5\ast \frac{8}{5}$.则1000的阶乘的5的个数为200+40+8+1 = 249个
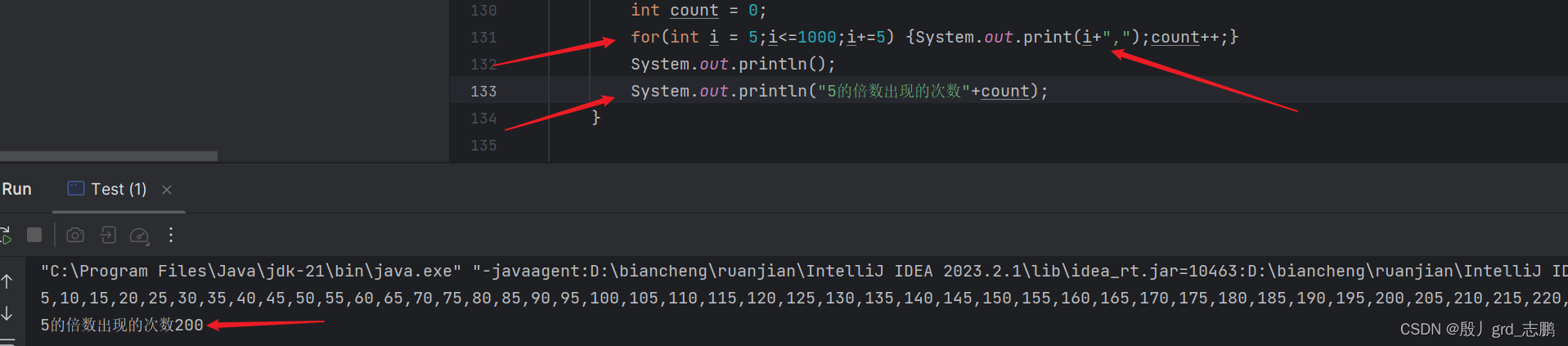
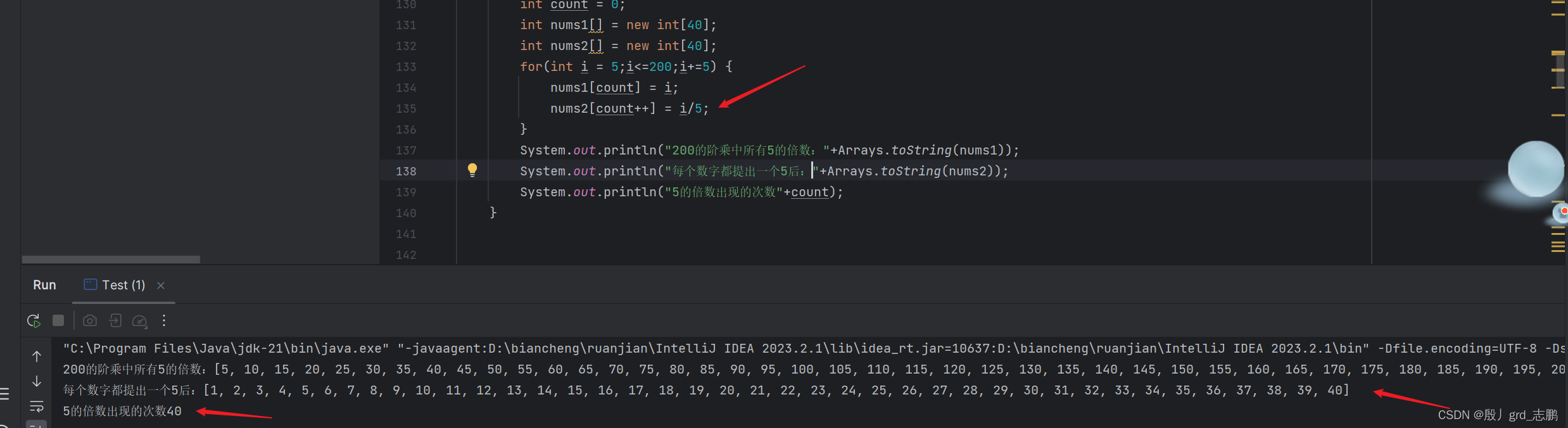
2. 为什么对单个数字1000不断除5，可以求出1000的阶乘中5的个数呢？
3. 因为我们需要转变思路，从现在开始，我们要统计从1到1000中，5的倍数出现的次数。

1. 1到1000中，5的倍数出现200次, 200个5的倍数分别是$5,10,15,20,.....,1000$
   
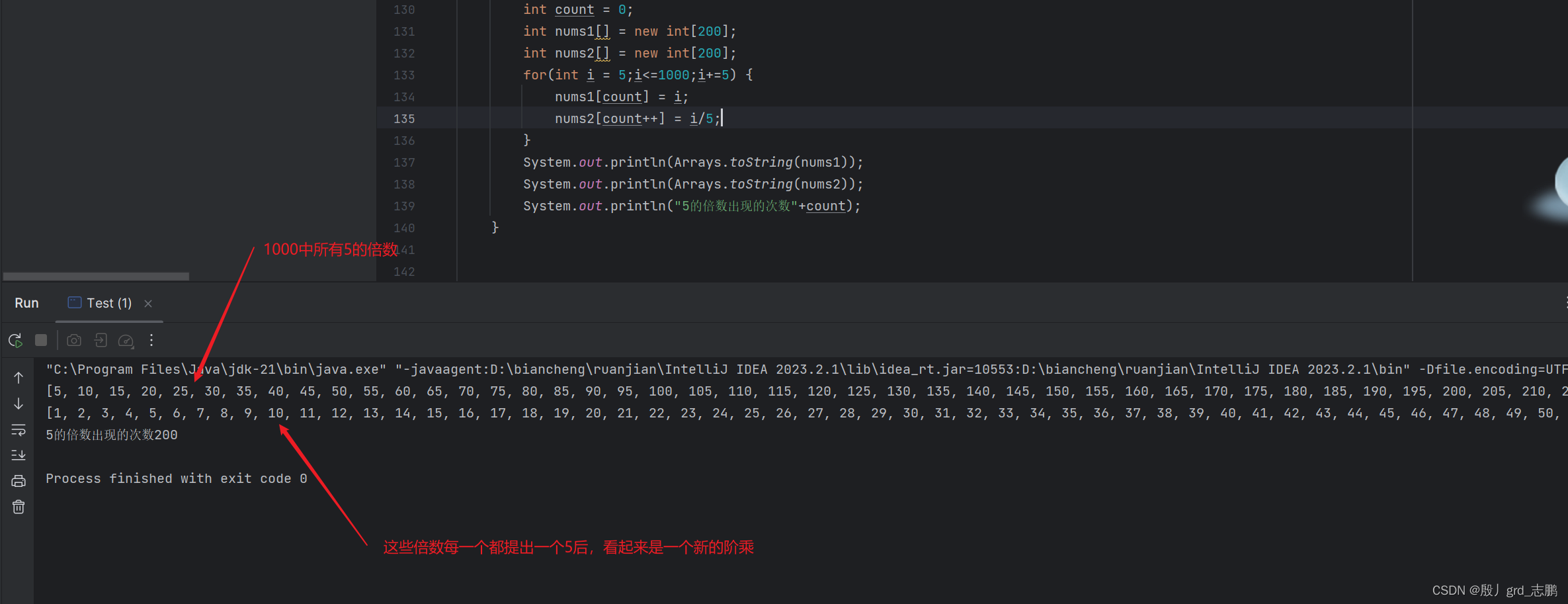
2. 此时如果我们将这200个5的倍数，全部提出一个5，就会获得200个5. 并且因式分解后剩下的值看起来如下：$1\ast 2\ast 3\ast 4\ast 5\ast ....\ast 200$,你会发现它们这些数正好组成了200的阶乘所有的数，
   

4. 此时，我们只需要从1到200这些数中，找当中5的倍数的个数。也就是$5,10,15,20,...,200$

1. 而200这个阶乘中，5的倍数共出现40次，我们将40次进行统计，然后继续对这40个5的倍数提出一个5的因子。你会发现它们又变成了40的阶乘。
   

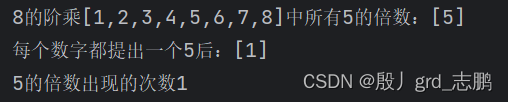
5. 此时继续求40这个阶乘中，5的倍数出现的次数。结果如下：共8个5的倍数，我们将8个5提出后，剩下的数字组成了8的阶乘
   
6. 继续对8求：共1个5的倍数5，提出1个5后，剩下数字只有1了，也就不用继续遍历了
   
7. 最终，就可以将所有我们提出的5统计起来，200+40+8+1 = 249个。

代码

class Solution {
    public int trailingZeroes(int n) {
        int count = 0;//统计个数
        while (n != 0){//只要n的阶乘中还可以有5就继续
            n /= 5;//获取n这个阶乘中所有5的倍数的个数
            count += n;//统计个数
        }
        return count;
    }
}