目录
1113. 红与黑--Flood Fill 算法---宽搜(BFS)或DFS)
输入格式
输出格式
数据范围
输入样例:
输出样例:
思路:
1.BFS 思路:
2.DFS 思路
方法一:(BFS)代码:
方法二:深搜(DFS)代码:
运行结果:
1113. 红与黑--Flood Fill 算法---宽搜(BFS)或DFS)
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。
你站在其中一块黑色的瓷砖上,只能向相邻(上下左右四个方向)的黑色瓷砖移动。
请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
输入格式
输入包括多个数据集合。
每个数据集合的第一行是两个整数 W 和 H,分别表示 x 方向和 y 方向瓷砖的数量。
在接下来的 HH 行中,每行包括 W 个字符。每个字符表示一块瓷砖的颜色,规则如下
1)‘.’:黑色的瓷砖;
2)‘#’:红色的瓷砖;
3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。
当在一行中读入的是两个零时,表示输入结束。
输出格式
对每个数据集合,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
数据范围
1≤W,H≤20
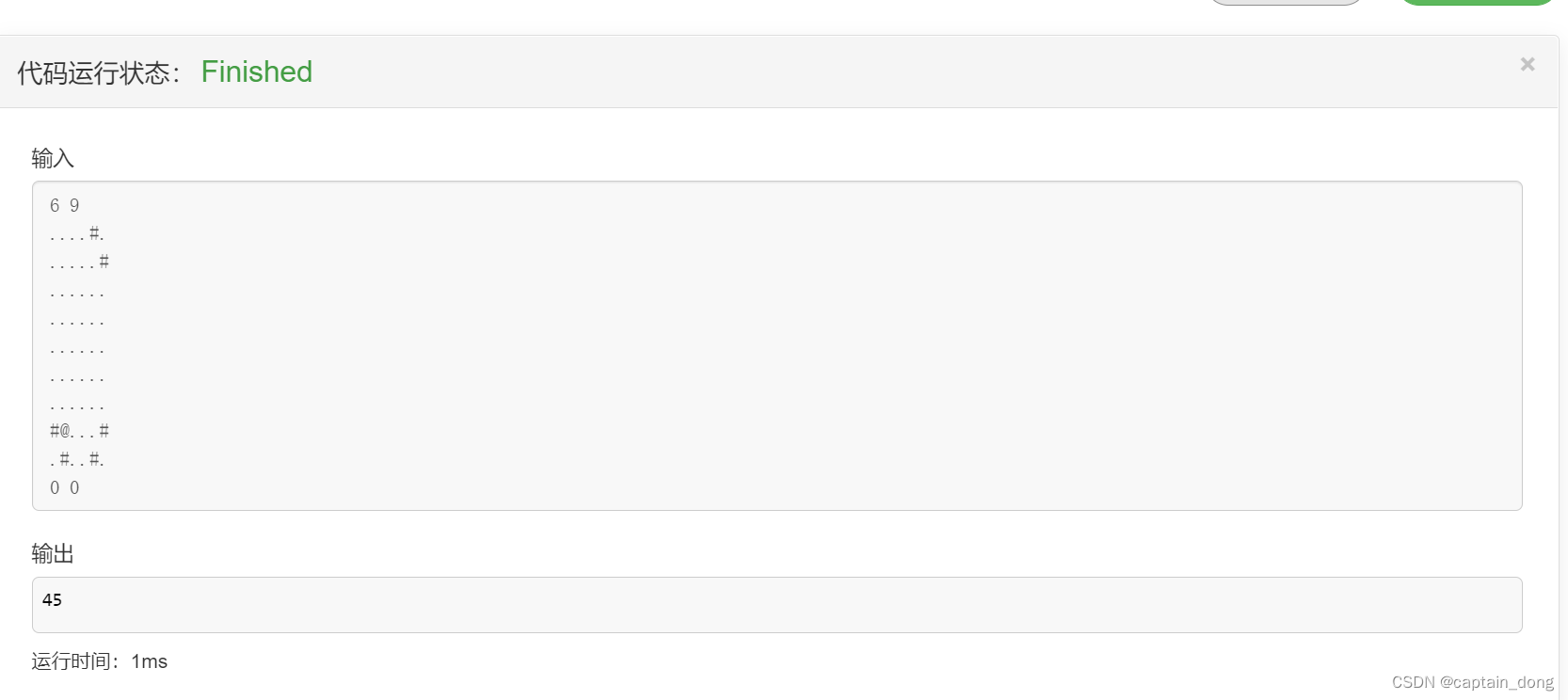
输入样例:
6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
0 0
输出样例:
45
| 难度:简单 |
| 时/空限制:1s / 64MB |
| 总通过数:31526 |
| 总尝试数:54082 |
| 来源: 《信息学奥赛一本通》 |
| 算法标签 DFSFlood Fill |
思路:
1.BFS 思路:

偏移量:

2.DFS 思路
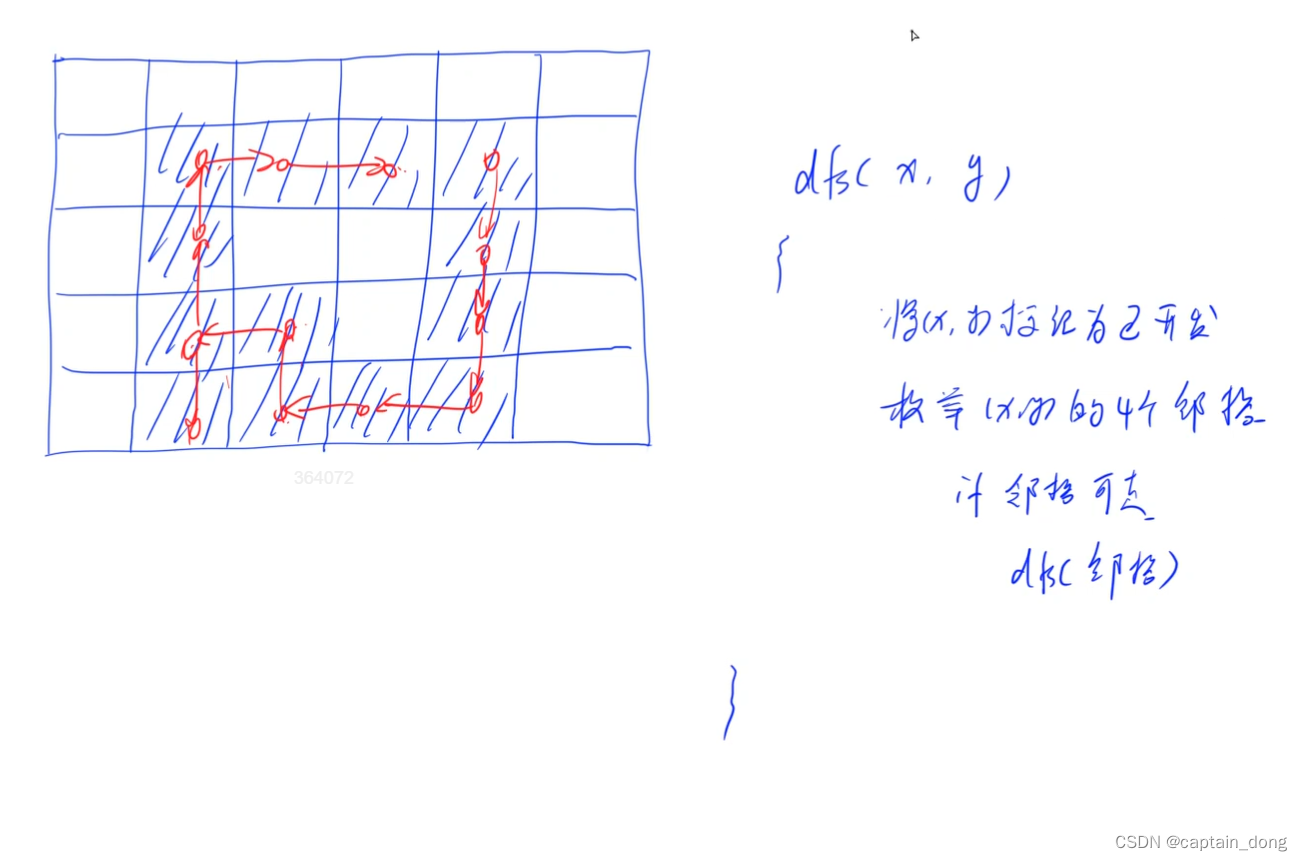
方法一:(BFS)代码:
#include <bits/stdc++.h>
// 定义宏,便于快速访问 pair 类型中的元素
#define x first
#define y second
// 引入标准命名空间
using namespace std;
// 定义 pair 类型别名 PII,表示一对整数
typedef pair<int, int> PII;
// 定义常量 N,表示矩阵的最大尺寸
const int N = 25;
// 定义全局变量 g(存储矩阵)、n(矩阵行数)、m(矩阵列数)
char g[N][N];
int n, m; // 矩阵行与列
// 定义偏移量数组 dx 和 dy,用于计算相邻格子的坐标
int dx[4] = {-1, 0, 1, 0}; // 每个方向x方向的偏移量:上、右、下、左
int dy[4] = {0, 1, 0, -1}; // 每个方向y方向的偏移量:上、右、下、左
// 广度优先搜索(BFS)函数,参数:起始位置的行坐标 sx 和列坐标 sy
// 返回值:从起始位置开始,能够搜索到的点(值为 '.') 的数量
int bfs(int sx, int sy) {
queue<PII> q; // 定义队列 q,用于存储待访问的格子坐标
q.push({sx, sy}); // 将起始位置加入队列
g[sx][sy] = '#'; // 将起始位置标记为 '#'
int res = 0; // 初始化搜索到的点的数量为 0
// 当队列不为空时,持续进行广度优先搜索
while (!q.empty()) {
auto t = q.front(); // 取队首元素(当前待访问的格子坐标)
q.pop(); // 出队,移除已访问的格子坐标
res++; // 计数器加一,表示找到一个可搜索的点
// 遍历当前格子的四个相邻格子
for (int i = 0; i < 4; i++) {
int x = t.x + dx[i], y = t.y + dy[i]; // 计算相邻格子的坐标
// 检查相邻格子是否在矩阵范围内、是否为 '.',若不符合条件则跳过
if (x < 0 || x >= n || y < 0 || y >= m || g[x][y] != '.') continue;
g[x][y] = '#'; // 将相邻格子标记为 '#',表示已访问
q.push({x, y}); // 将相邻格子坐标加入队列,等待后续访问
}
}
return res; // 返回搜索到的点的数量
}
int main() {
// 循环读取多组测试数据,直到输入为 0 0
while (cin >> m >> n, n || m) {
// 读取当前矩阵数据
for (int i = 0; i < n; i++) cin >> g[i];
// 查找矩阵中 '@'(起始位置)的坐标
int x, y;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (g[i][j] == '@') {
x = i;
y = j;
}
// 调用 BFS 函数,计算并输出能够搜索到的点的数量
cout << bfs(x, y) << endl;
}
return 0; // 主函数返回 0,表示程序正常结束
}方法二:深搜(DFS)代码:
#include <bits/stdc++.h>
using namespace std;
// 定义全局变量 n(矩阵行数)、m(矩阵列数),以及矩阵 g
int n, m;
const int N = 25;
char g[N][N];
// 定义偏移量数组 dx 和 dy,用于计算相邻格子的坐标
int dx[4] = {-1, 0, 1, 0}; // 水平方向的偏移量:左、中心、右、中心
int dy[4] = {0, 1, 0, -1}; // 垂直方向的偏移量:上、中心、下、中心
// 深度优先搜索(DFS)函数,参数:当前格子的行坐标 x 和列坐标 y
// 返回值:以当前格子为根的连通区域中值为 '.' 的点的数量
int dfs(int x, int y) {
int res = 1; // 初始化结果为 1,表示当前格子本身是一个可搜索的点
g[x][y] = '#'; // 将当前格子标记为 '#',表示已访问
// 遍历当前格子的四个相邻格子
for (int i = 0; i < 4; i++) {
int a = x + dx[i]; // 计算相邻格子的行坐标
int b = y + dy[i]; // 计算相邻格子的列坐标
// 检查相邻格子是否在矩阵范围内、是否为 '.',若符合条件则递归搜索
if (a >= 0 && a < n && b >= 0 && b < m && g[a][b] == '.')
res += dfs(a, b); // 将相邻格子的搜索结果累加到 res
}
return res; // 返回以当前格子为根的连通区域中值为 '.' 的点的数量
}
int main() {
// 循环读取多组测试数据,直到输入为 0 0
while (cin >> m >> n, n || m) {
// 读取当前矩阵数据
for (int i = 0; i < n; i++) cin >> g[i];
// 查找矩阵中 '@'(起始位置)的坐标
int x, y;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (g[i][j] == '@') {
x = i;
y = j;
}
// 调用 DFS 函数,计算并输出以起始位置为根的连通区域中值为 '.' 的点的数量
cout << dfs(x, y) << endl;
}
return 0; // 主函数返回 0,表示程序正常结束
}实现了一个简单的深度优先搜索(DFS)算法,用于在一个给定的矩阵中,从标记为
'@'的起始位置开始,搜索并标记所有相邻且值为'.'的点。最终输出以起始位置为根的连通区域中值为'.'的点的数量。
运行结果: