摘要
本章主要是说一下gdb的使用,以及把使用指令放入放个指令手册。
目录
摘要
一、背景
二、使用
1、产生debug文件
2、进入gdb
3、使用指令
三、思维导图
一、背景
Linux调试器gdb的背景主要涉及到Linux程序发布方式和调试需求。
在Linux中,程序的发布方式主要有两种:debug(调试)模式和release(发行)模式。由gcc/g++生成的二进制程序,默认是release模式,这种模式下的程序不会添加任何调试信息,因此是不可调试的。而gdb正是为了满足Linux程序的调试需求而存在的工具。
gdb是Linux中的调试器,由于Linux是命令行式的操作,所以进行调试也是以命令行的方式进行。尽管在某些场景下,命令行方式的调试可能没有IDE下的调试来得简洁利索,但在没有设计专门的IDE的场景下,gdb就发挥了其重要的作用。
总的来说,gdb在Linux系统中扮演着至关重要的角色,为开发者提供了强大的调试功能,帮助他们有效地查找和修复程序中的错误。
二、使用
1、产生debug文件
这个只需要在gcc编译文件的时候加上-g就可以了如下方代码
[ly1@VM-24-9-centos test]$ gcc -g -o test.debug test.c
[ly1@VM-24-9-centos test]$ ll
total 40
-rwxrwxr-x 1 ly1 ly1 8360 Apr 12 20:49 hello
-rw-rw-r-- 1 ly1 ly1 643 Apr 12 20:45 LICENSE
-rw-rw-r-- 1 ly1 ly1 841 Apr 12 20:45 README.en.md
-rw-rw-r-- 1 ly1 ly1 930 Apr 12 20:45 README.md
-rw-rw-r-- 1 ly1 ly1 0 Apr 12 21:23 test2
-rw-rw-r-- 1 ly1 ly1 0 Apr 12 21:20 test3.c
-rw-rw-r-- 1 ly1 ly1 70 Apr 12 20:48 test.c
-rwxrwxr-x 1 ly1 ly1 9360 Apr 12 21:51 test.debug
[ly1@VM-24-9-centos test]$
2、进入gdb
gdb +需要调试的程序,如下方代码,就是gdb test.debug就是可以进入gdb如下方。
[ly1@VM-24-9-centos test]$ gdb test.debug
GNU gdb (GDB) Red Hat Enterprise Linux 7.6.1-120.el7
Copyright (C) 2013 Free Software Foundation, Inc.
License GPLv3+: GNU GPL version 3 or later <http://gnu.org/licenses/gpl.html>
This is free software: you are free to change and redistribute it.
There is NO WARRANTY, to the extent permitted by law. Type "show copying"
and "show warranty" for details.
This GDB was configured as "x86_64-redhat-linux-gnu".
For bug reporting instructions, please see:
<http://www.gnu.org/software/gdb/bugs/>...
Reading symbols from /home/ly1/test/test.debug...done.
(gdb)
3、使用指令
下面就不一一演示了,我把能用到的都罗列出来了,如下方代码块里面所示
list/l 行号:显示binFile源代码,接着上次的位置往下列,每次列10行。
list/l 函数名:列出某个函数的源代码。
r或run:运行程序。
n 或 next:单条执行。
s或step:进入函数调用
break(b) 行号:在某一行设置断点
break 函数名:在某个函数开头设置断点
info break :查看断点信息。
finish:执行到当前函数返回,然后挺下来等待命令
print(p):打印表达式的值,通过表达式可以修改变量的值或者调用函数
p 变量:打印变量值。
set var:修改变量的值
continue(或c):从当前位置开始连续而非单步执行程序
run(或r):从开始连续而非单步执行程序
delete breakpoints:删除所有断点
delete breakpoints n:删除序号为n的断点
disable breakpoints:禁用断点
enable breakpoints:启用断点
info(或i) breakpoints:参看当前设置了哪些断点
display 变量名:跟踪查看一个变量,每次停下来都显示它的值
undisplay:取消对先前设置的那些变量的跟踪
until X行号:跳至X行
breaktrace(或bt):查看各级函数调用及参数
info(i) locals:查看当前栈帧局部变量的值
quit:退出gdb
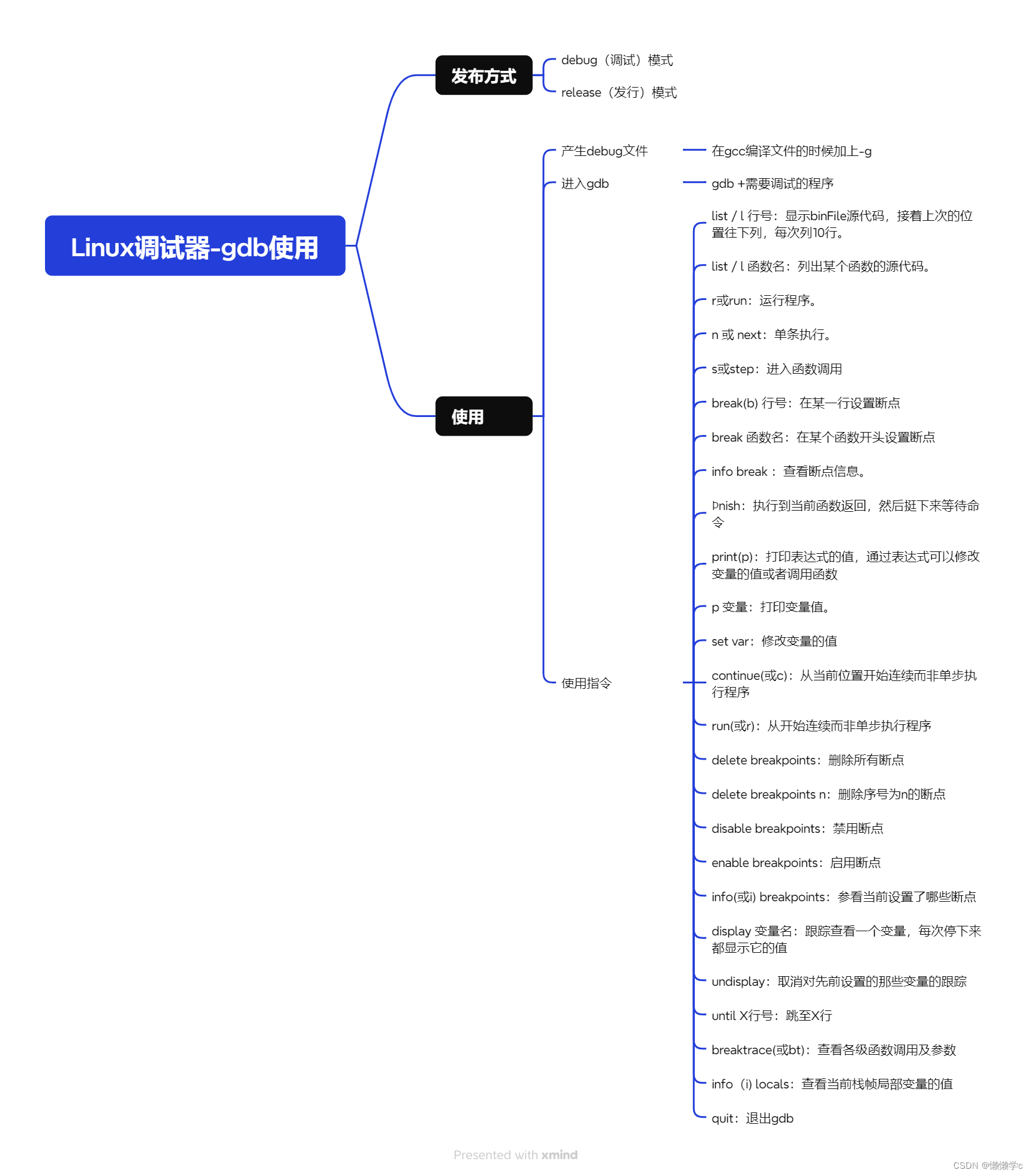
三、思维导图