【数据结构】稀疏矩阵的快速转置

news2025/4/3 4:07:25

【数据结构】稀疏矩阵的转置（普通转置和快速转置）

三元表

三元表结构：
在这里插入图片描述

//三元表结构：
typedef struct{  
    int i, j;       //非零元的行、列下标 
    int e;   //非零元的值
} Triple;

//稀疏矩阵的结构
#define MAXSIZE 100  //非零元最大个数
typedef struct{  
    Triple data[MAXSIZE + 1];       //三元组表，data[0]未用
    int mu, nu, tu; //矩阵行、列数、非零元个数
} TSMatrix;

特点：
有序的双下标法行序有序存储
便于进行依行顺序处理的矩阵运算
若需存取某一行中的非零元，需**从头开始查找**。
非零元以行为主序顺序存放

压缩存储后，元素aij的存储位置与其下标无关，而取决于之前的非零元个数。

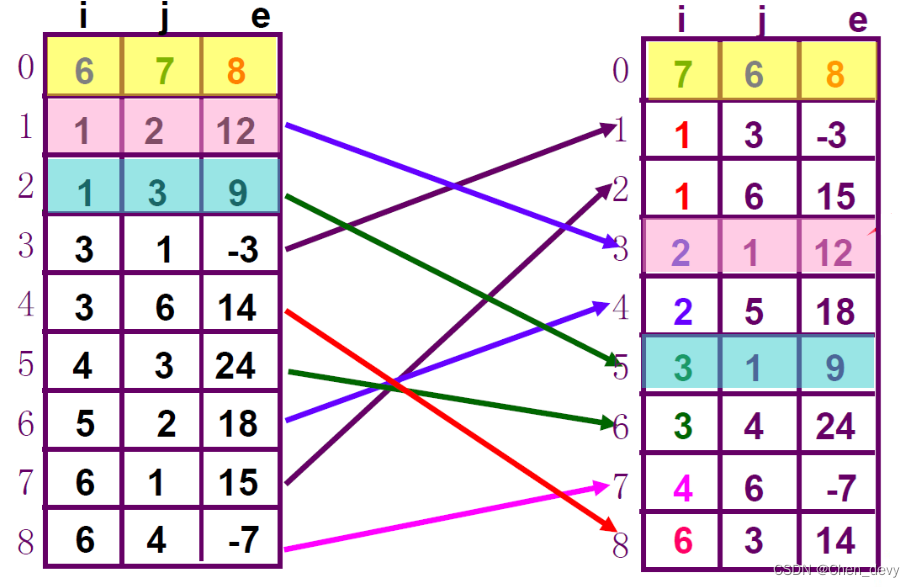
稀疏矩阵的转置

解决思路：

将矩阵行、列维数互换，非零元个数不变
将每个三元组中的i和j相互调换，非零元值不变
重排次序，使T.data中元素以T的行(M的列)为主序

方法一（普通转置）复杂度为O(T.mu×T.nu)

转置运算：一个 m * n 的矩阵 M ，其对应的转置矩阵是一个 n * m 的矩阵 T ，并且 T 中的元素 T(i, j) 与 B 中的元素 M(j, i) 对应相等。

我们需要将三元组的行列互换，要构造一个转置矩阵 T 的三元组表，并且这个三元组表中的次序也要满足按照行为主序排列，按照列为次序排列。
由于 T 中的行对应的是 M 中的列，所以在转置过程中，我们需要顺序枚举每一列。
所以普通的稀疏矩阵转置方法为：
（1）按矩阵T中三元组表T.data的次序依次在矩阵M的三元组表M.data中找到相应三元组进行转置
（2）为找到M.data中第i列所有非零元素，需对M.data扫描一遍
（3）由于M.data以M行序为主序，所以得到的恰是T.data中应有的顺序

//复杂度为O(T.mu×T.nu)
Status TransposeSMatrix(TSMatrix M, TSMatrix &T){ 
    int col, p, k;
    T.mu=M.nu;  
    T.nu=M.mu; 
    T.tu=M.tu; 
    if(T.tu){ //有非零元，转置
        k=1;//k为T.data表下标
        for(col=1;col<=M.nu;col++)//查找M每一列的非零元
            for( p=1;p<=M.tu;p++)//扫描M的所有非零元
                if( M.data[p].j==col ){ 
                    T.data[k].i=M.data[p].j;
                    T.data[k].j=M.data[p].i;
                    T.data[k].e=M.data[p].e; 
                    k++;
                }
        return OK;
    }
    return ERROR;
}

//T(n)=O(M.nu×M.tu)
//若M.tu与M.mu×M.nu同数量级则 T(n)=O(M.mu×M.nu^2)

方法二：快速转置复杂度O(S.nu+S.tu)

定义一个数组num[] 来记录原矩阵 M 中每一列非零元的个数，同时再定义一个数组 cpot[] 用来记录 M 中每一列第一个非零元在T 中对应的位置。

首先，我们定义两个辅助数组：
num[]：用于记录原矩阵 M 中每一列非零元素的个数。
cpot[]：用于记录 M 中每一列第一个非零元素在转置矩阵 T 中对应的位置。
扫描原矩阵 M 三次：
第一次：记录元素矩阵 S 中每列的非零元素个数，并存储在 num[] 中。
第二次：计算每列第一个非零元素在新矩阵 T 中的首位置，并存储在 cpot[] 中。
第三次：根据 cpot[] 的信息，将原矩阵 M 转置到新矩阵 T 中。
在转置过程中，我们遍历原矩阵 M 的每一个非零元素，根据其列号找到在新矩阵 T 中的正确位置，并将元素交换到该位置。

具体代码加注释如下：

//复杂度O(S.nu+S.tu) 
//若S.tu与S.mu×S.nu同数量级则 T(n)=O(S.mu×S.nu)
void TransPose_F(TSMatrix S,TSMatrix &Transpose_S){
    //S为原来矩阵
    //Transpose_S为转置后矩阵
    Transpose_S.mu=S.nu;
    Transpose_S.nu=S.mu;
    Transpose_S.tu=S.tu;
    if(S.tu){
        //判断是否为空
        int col;//列
        int num[MAXSIZE]={0};// 记录原三元组中列号为 col 的项的数目。 辅助数组
        int cpot[MAXSIZE]={0};// 记录原三元组中列号为 col 的项在新三元组中的首位置。 辅助数组
        
        //扫描第一次 记录元素矩阵S中列数为j的个数
        for(int i=1;i<=S.tu;i++){
            //记录元素矩阵S中列数为j的个数
            num[S.data[i].j]++;
        }

        cpot[1]=1;//初始化第一个元素的地址

        //扫描第二次 记录原三元组中列号为 col 的项在新三元组中的首位置
        for(col=2;col<=S.nu;col++){
            //列号为 col 的项在新三元组中的首位置
            cpot[col]=cpot[col-1]+num[col-1];
        }

        //扫描第三次 转置
        for(int t=1;t<=S.tu;t++){
            col=S.data[t].j;//列数
            int s=cpot[col];//地址  下标

            Transpose_S.data[s].e=S.data[t].e;
            Transpose_S.data[s].i=S.data[t].j;
            Transpose_S.data[s].j=S.data[t].i;

            cpot[col]++;//下标 后移
        }
    }
}