LeetCode-62. 不同路径【数学 动态规划 组合数学】
- 题目描述:
- 解题思路一:动态规划,动规五部曲
- 解题思路二:动态规划(版本二)
- 解题思路三:数论
题目描述:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
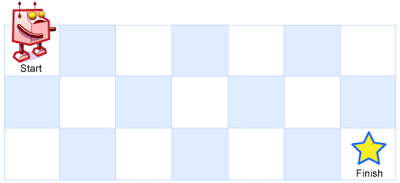
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右
- 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109
解题思路一:动态规划,动规五部曲
-
确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。 -
确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
-
dp数组的初始化
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。 -
确定遍历顺序
这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
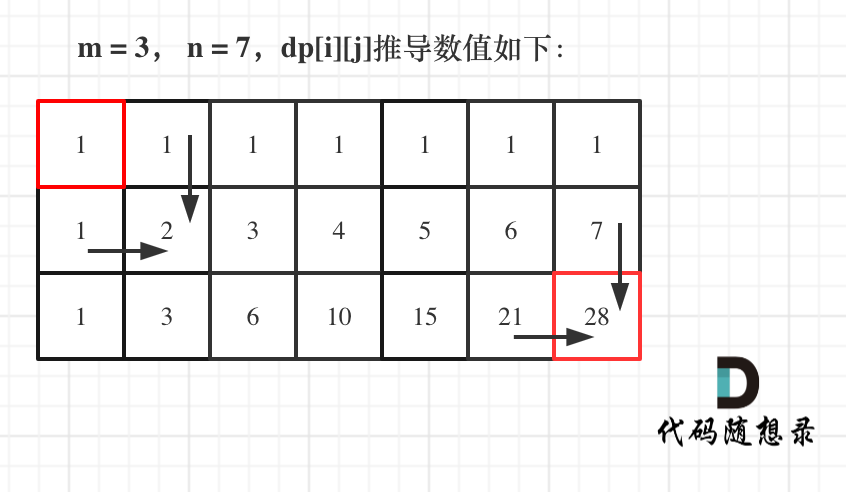
- 举例推导dp数组
如图所示:
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
# 创建一个二维列表用于存储唯一路径数
dp = [[0] * n for _ in range(m)]
# 设置第一行和第一列的基本情况
for i in range(m):
dp[i][0] = 1
for j in range(n):
dp[0][j] = 1
# 计算每个单元格的唯一路径数
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
# 返回右下角单元格的唯一路径数
return dp[m - 1][n - 1]
时间复杂度:O(nm)
空间复杂度:O(nm)
解题思路二:动态规划(版本二)
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
# 创建一个一维列表用于存储每列的唯一路径数
dp = [1] * n
# 计算每个单元格的唯一路径数
for j in range(1, m):
for i in range(1, n):
dp[i] += dp[i - 1]
# 返回右下角单元格的唯一路径数
return dp[n - 1]
时间复杂度:O(nm)
空间复杂度:O(n)
解题思路三:数论
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。
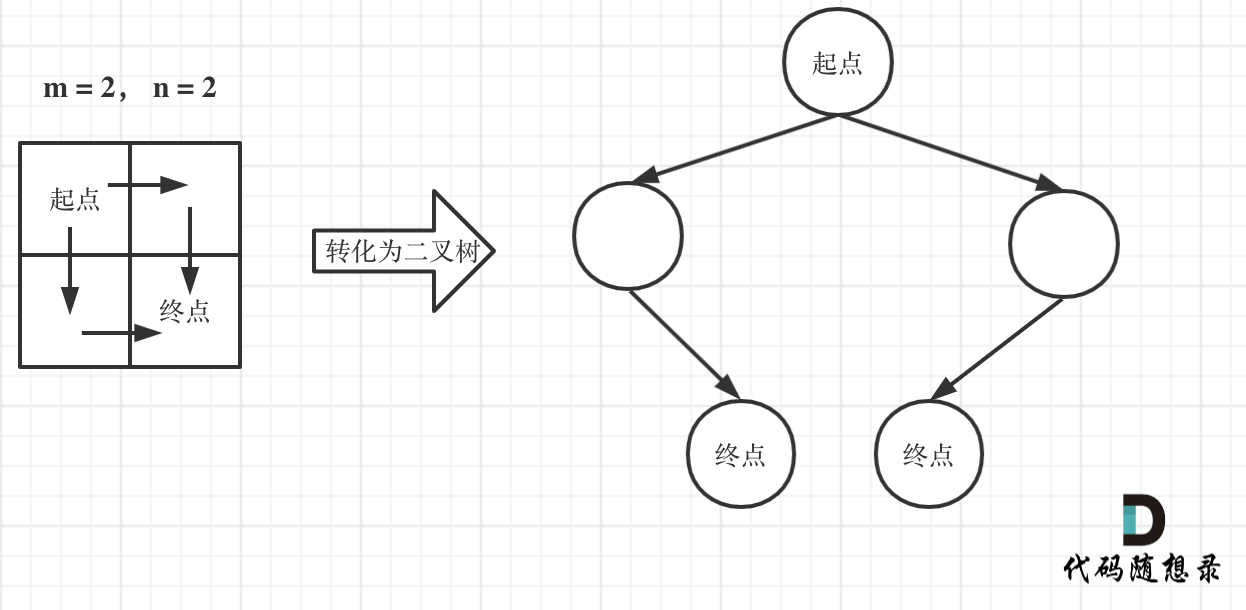
在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
那么有几种走法呢? 可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
那么这就是一个组合问题了。
那么答案,如图所示:
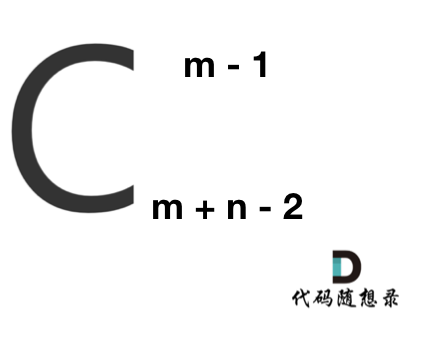
求组合的时候,要防止两个int相乘溢出! 所以不能把算式的分子都算出来,分母都算出来再做除法。
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
numerator = 1 # 分子
denominator = m - 1 # 分母
count = m - 1 # 计数器,表示剩余需要计算的乘积项个数
t = m + n - 2 # 初始乘积项
while count > 0:
numerator *= t # 计算乘积项的分子部分
t -= 1 # 递减乘积项
while denominator != 0 and numerator % denominator == 0:
numerator //= denominator # 约简分子
denominator -= 1 # 递减分母
count -= 1 # 计数器减1,继续下一项的计算
return numerator # 返回最终的唯一路径数
时间复杂度:O(m)
空间复杂度:O(1)