在赶一篇作业出来
第一个：
题目：编程实现，求s=a+aa+aaa+aa⋯an个a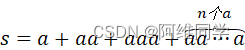
的值，其中a是一个数字。例如当a为2，n为5时，计算，2＋22＋222＋2222＋22222的值。
#include<stdio.h>
int main()
{
printf("请输入a和n\n");
int a,n,k,t=0,s=0;
scanf("%d%d", &a ,& n);
for ( k=1; k<=n; k++)
{
t = t* 10 + a;
s += t;
}
printf("结果为：%d", s);
return 0;
}输入测试数据：2 5 （其中a=2,n=5）
程序运行结果：24690
解释：
这里定义了五个整数变量：
a和n用于存储用户输入的两个整数。k用作for循环的计数器。t用于存储当前迭代的a的重复值（例如，当a=2且k=3时，t=222）。s用于存储整个序列的和。
提示用户输入：
c复制代码
printf("请输入a和n\n");使用
printf函数输出提示信息，告诉用户输入两个整数a和n。
读取用户输入
c复制代码
scanf("%d%d", &a ,& n);使用
scanf函数读取用户输入的两个整数，并存储在变量a和n中。
计算序列的和：
c复制代码
for ( k=1; k<=n; k++){t = t* 10 + a;s += t;}这是一个
for循环，它执行n次。在每次迭代中：
t被更新为t乘以10再加上a。这样，t的值就变成了a重复k次的结果。例如，当a=2且k=3时，t的值会从2变为22，再变为222。s加上当前的t值，从而累计序列的和
第二个：
题目：编程实现，输入一行字符，分别统计出其中英文字母，空格，数字和其它字符的个数(以\n作为结束)。
输入测试数据：abcd !@# 123 EFG 890 *&^
程序运行结果：英文字符的个数：7,空格的个数：5,
数字字符的个数：6,其它字符的个数：6
#include <stdio.h>
int main()
{
int m = 0, n = 0, o = 0, p = 0;
char c;
printf("请输入字符串：");
// 使用getchar直接读取字符串，不使用scanf （知识点）
while ((c = getchar()) != '\n')
{
if (c >= 'A' && c <= 'Z' || c >= 'a' && c <= 'z')
m += 1;
else if (c >= '0' && c <= '9')
n += 1;
else if (c == ' ')
o += 1;
else
p += 1;
}
printf("英文字符的个数：%d\n", m);
printf("数字字符的个数：%d\n", n);
printf("空格的个数：%d\n", o);
printf("其它字符的个数：%d\n", p);
return 0;
}AI的解释：
这里定义了四个整数变量
m,n,o,p，用于分别统计英文字符、数字字符、空格和其他字符的数量。还定义了一个字符变量c，用于存储从输入中读取的单个字符。提示用户输入：
c复制代码
printf("请输入字符串：");使用
printf函数输出提示信息，告诉用户输入一个字符串。读取字符并统计：
while ((c = getchar()) != '\n'){...}这是一个
while循环，使用getchar函数逐个读取用户输入的字符，直到遇到换行符\n为止。在循环内部，程序使用
if-else if-else结构来判断字符的类型，并相应地增加计数器的值。
- 如果字符是英文字符（大写或小写），
m增加1。- 如果字符是数字字符，
n增加1。- 如果字符是空格，
o增加1。- 对于其他类型的字符，
p增加1。- 输出结果
c复制代码
printf("英文字符的个数：%d\n", m);printf("数字字符的个数：%d\n", n);printf("空格的个数：%d\n", o);printf("其它字符的个数：%d\n", p);
第三个：（这个还是得再看看）双循环
题目：编程实现，利用双循环编程，输出下列所示的图形。
代码如下：
#include <stdio.h>
int main() {
int i, j;
int m = 6; // 根据图形确定星号的最大数量
// 上半部分：星号数量逐渐增加
for (i = 1; i <= m; i++) {
// 打印空格
for (j = 1; j <= m - i; j++) {
printf(" ");
}
// 打印星号
for (j = 1; j <= i; j++) {
printf("*");
}
printf("\n"); // 换行
}
// 下半部分：星号数量逐渐减少（排除中间的星号最多的那一行）
for (i = m - 1; i > 0; i--) {
// 打印空格
for (j = 1; j <= m - i; j++) {
printf(" ");
}
// 打印星号
for (j = 1; j <= i; j++) {
printf("*");
}
printf("\n"); // 换行
}
return 0;下面那部分，重新看一下有不一样的收获：（运行下面有解释。）
运行结果：（520的尺寸，保准喜欢）
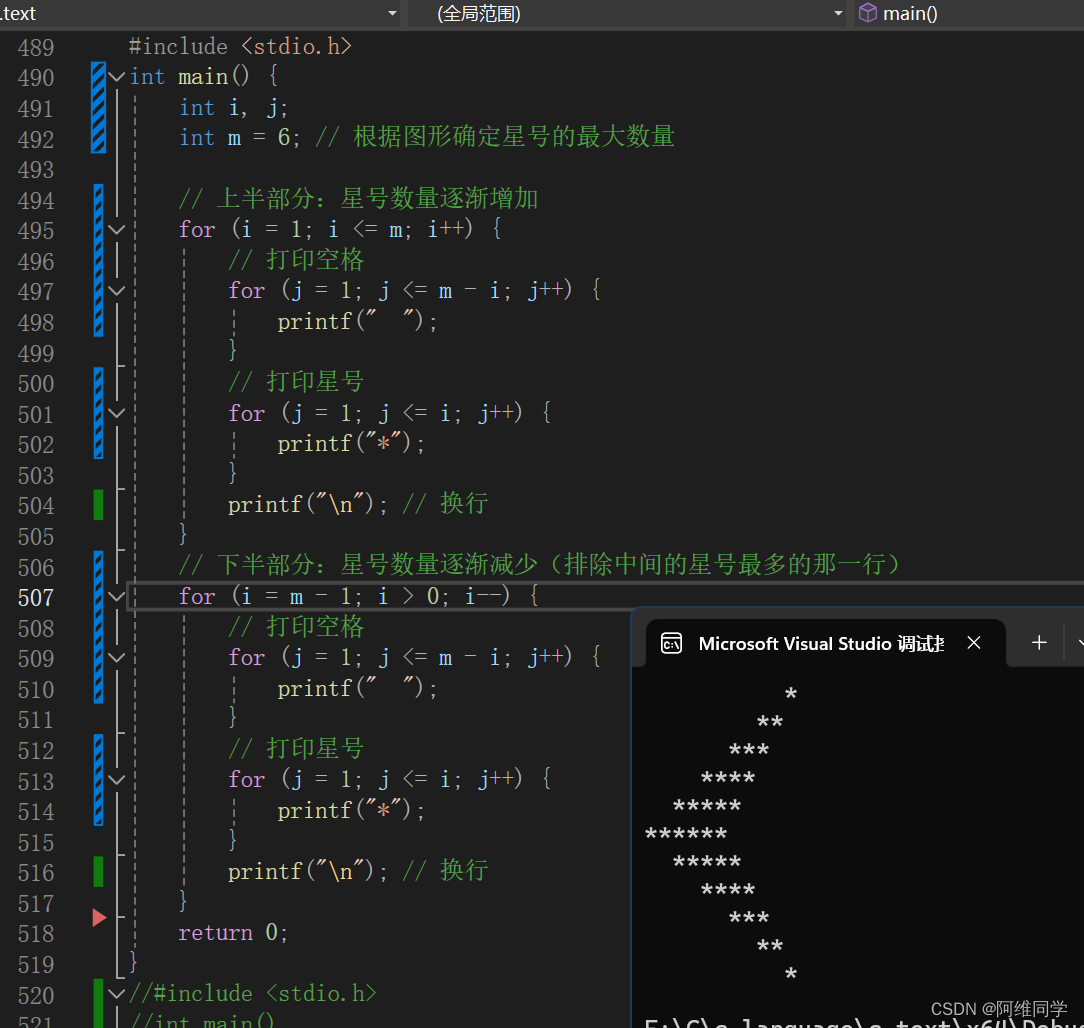
变量定义
c复制代码
int i, j;int m = 6; // 根据图形确定星号的最大数量这里定义了两个循环变量
i和j，以及一个常量m，用于表示等腰三角形每一行星号的最大数量。打印等腰三角形的上半部分
c复制代码
for (i = 1; i <= m; i++) {外层循环控制行数，从1到
m。
c复制代码
for (j = 1; j <= m - i; j++) {printf(" ");}内层循环用于打印每一行前面的空格。随着行数
i的增加，空格的数量逐渐减少，从而实现等腰三角形的形状。
c复制代码
for (j = 1; j <= i; j++) {printf("*");}另一个内层循环用于打印星号。随着行数
i的增加，星号的数量逐渐增加。
c复制代码
printf("\n"); // 换行每一行星号打印完后，换行以开始下一行的打印。
打印等腰三角形的下半部分（排除中间行）
c复制代码
for (i = m - 1; i > 0; i--) {外层循环控制行数，从
m-1递减到1（不包括0，因为中间那一行已经打印过了）。接下来的内层循环和打印逻辑与上半部分类似，只是方向相反：随着行数
i的减少，空格的数量逐渐增加，星号的数量逐渐减少。
第四个：
这个直接把我电脑给干关机了：虽然我问C语言老师说找不到，但是我从历史文件头给他扒出来了
开开机就成这种样子。哈哈哈哈哈：。有点扯淡，所以我给他设了250的尺寸
但是还是给你们发一下题目，哈哈哈哈
题目：用一张一元票换1分、2分和5分的硬币30枚（至少各一枚），问有哪几种换法（各几枚）。（提示：本题用穷举法编程）。
程序运行结果：
2 14 14
5 10 15
8 6 16
11 2 17
这个代码如下：
#include<stdio.h>
int main()
{
int i, j, k;
int n=0 ;
for (i = 1; i <= 27; i++)
{
for (j = 1; j <= 30-i; j++)
{
k = 30-i-j;
if (i + (j * 2) + (k * 5) == 100 && (i * j * k) != 0)
{
printf("%d %d %d \n ", i, j, k);
n++;
}
}
}
printf("共%d种配法",n);
return 0;
}主要目的是寻找一组三元整数组合
(i, j, k)，这组数满足以下两个条件：
i + 2j + 5k = 100i * j * k ≠ 0外层循环：
c复制代码
for (i = 1; i <= 27; i++)
i的值从1遍历到27。这是因为考虑到i + 2j + 5k = 100这个等式，如果i的值太大，那么j和k的值将可能为负或零，这不符合题目的要求。内层循环：
c复制代码
for (j = 1; j <= 30-i; j++)对于每一个
i的值，j的值从1遍历到30-i。这是因为i + 2j的最大值不能超过100，所以j的最大值不能超过50-i，但考虑到k的存在，这里取了30-i作为上限。计算k的值：
c复制代码
k = 30-i-j;根据
i + 2j + 5k = 100这个等式，我们可以解出k的值。条件判断：
c复制代码
if (i + (j * 2) + (k * 5) == 100 && (i * j * k) != 0)判断当前
(i, j, k)的组合是否满足i + 2j + 5k = 100并且i * j * k ≠ 0。打印和计数：
c复制代码
printf("%d %d %d \n", i, j, k);n++;如果当前组合满足条件，则打印该组合，并增加计数器
n的值。输出总的组合数：
c复制代码
printf("共%d种配法", n);在所有可能的组合遍历完之后，输出满足条件的组合的总数。
第5个：就最大公约数，最小公倍数
最后一个了，能看尽量看下去，哈哈哈
题目：编写程序：输入两个正整数，求其最大公约数和最小公倍数。
输入测试数据：12 8
程序运行结果：最大公约数为4，最小公倍数为24
程序如下
#include <stdio.h>
int main()
{
int a, b ,i;
scanf("%d%d", &a, &b);
int min = (a < b) ? a : b;
for (i= min; i >0; i--)
{
if (a % i == 0 && b % i == 0)
break;
}
printf("最大公约数是:%d", i);
int m;
m = (a * b) / (i); // 查到的公式,简洁快捷就用它了
printf("最小公倍数是：%d", m);
}也可以看一下解释
变量定义
c复制代码
int a, b, i;这里定义了三个整数变量
a、b和i，分别用于存储用户输入的两个整数以及用于循环和计算的临时变量。读取用户输入
c复制代码
scanf("%d%d", &a, &b);这一行使用
scanf函数从标准输入读取两个整数，并存储在变量a和b中。计算最小数
c复制代码
int min = (a < b) ? a : b;这里使用三元运算符计算
a和b中的较小值，并将其存储在变量min中。这个较小值将作为循环的起始值，用于寻找两个数的最大公约数。寻找最大公约数
c复制代码
for (i = min; i > 0; i--){if (a % i == 0 && b % i == 0)break;}这个循环从
min开始递减，检查每个数是否同时是a和b的约数。如果是，循环将终止，此时i的值就是a和b的最大公约数。打印最大公约数
c复制代码
printf("最大公约数是:%d", i);使用
printf函数输出计算得到的最大公约数。计算最小公倍数
c复制代码
int m;m = (a * b) / i;最小公倍数（LCM）可以通过两个数的乘积除以它们的最大公约数来计算。这里，
m被初始化为a和b的乘积除以i（即最大公约数）的结果。
还有其他好几种方法可可解决，下面列一下;AI助力
除了上述方法外，还有其他方法可以计算两个数的最小公倍数（LCM）。以下是一些替代方法：
方法一：直接使用公式
最小公倍数（LCM）和最大公约数（GCD）之间有一个简单的数学关系，可以直接用公式计算：
c复制代码
LCM(a, b) = (a * b) / GCD(a, b)其中，
GCD(a, b)表示a和b的最大公约数。因此，你可以先计算GCD，然后用这个公式得到LCM。方法二：质因数分解
将两个数分别进行质因数分解，然后找出所有质因数的最高次幂，将它们相乘得到最小公倍数。
例如，对于
a = 12和b = 18：
12 = 2^2 * 318 = 2 * 3^2最小公倍数
LCM(12, 18) = 2^2 * 3^2 = 36。方法三：逐个倍数查找
这种方法效率较低，但对于较小的数或者教学目的仍然有效。你可以从较大的数开始，逐个检查它是否是两个数的倍数，直到找到为止。
c复制代码
int lcm(int a, int b) {int max = (a > b) ? a : b;while (1) {if (max % a == 0 && max % b == 0) {return max;}max++;}}这个函数会一直增加
max的值，直到找到一个数能同时被a和b整除。虽然这种方法可行，但它不是最高效的，特别是当a和b很大时。方法四：使用欧几里得算法和扩展欧几里得算法
欧几里得算法（辗转相除法）用于计算最大公约数，而扩展欧几里得算法可以用来同时找到最大公约数和对应的贝祖等式系数，进而可以通过这些系数计算最小公倍数。这种方法在数学上很优美，但实现起来相对复杂一些。
在实际编程中，推荐使用方法一，因为它既简单又高效。如果你需要处理大数或者对性能有较高要求，可以考虑使用专门的数学库或工具来计算最大公约数和最小公倍数。
走了走了，上课去了 待会就是c语言课。
祝大家好运！
