石子合并问题是经典的区间dp问题，我们需要枚举中间端点k的情况从而来推出dp数组的值。

---

前言

石子合并问题是经典的区间dp问题，我们需要枚举中间端点k的情况从而来推出dp数组的值。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、石子合并问题

设有 N 堆石子排成一排，其编号为 1,2,3,…,N。

每堆石子有一定的质量，可以用一个整数来描述，现在要将这 N堆石子合并成为一堆。

每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同。

例如有 4 堆石子分别为 1 3 5 2， 我们可以先合并 1、2 堆，代价为 4，得到 4 5 2， 又合并 1、2 堆，代价为 9，得到 9 2，再合并得到 11，总代价为 4+9+11=24；

如果第二步是先合并 2、3堆，则代价为 7，得到 4 7，最后一次合并代价为 11，总代价为 4+7+11=22。

问题是：找出一种合理的方法，使总的代价最小，输出最小代价。

二、算法思路

1.问题思路

我们引入二维数组dp，dp[i][j]表示的含义是从第i堆，合并到第j堆所需要的最小代价数。

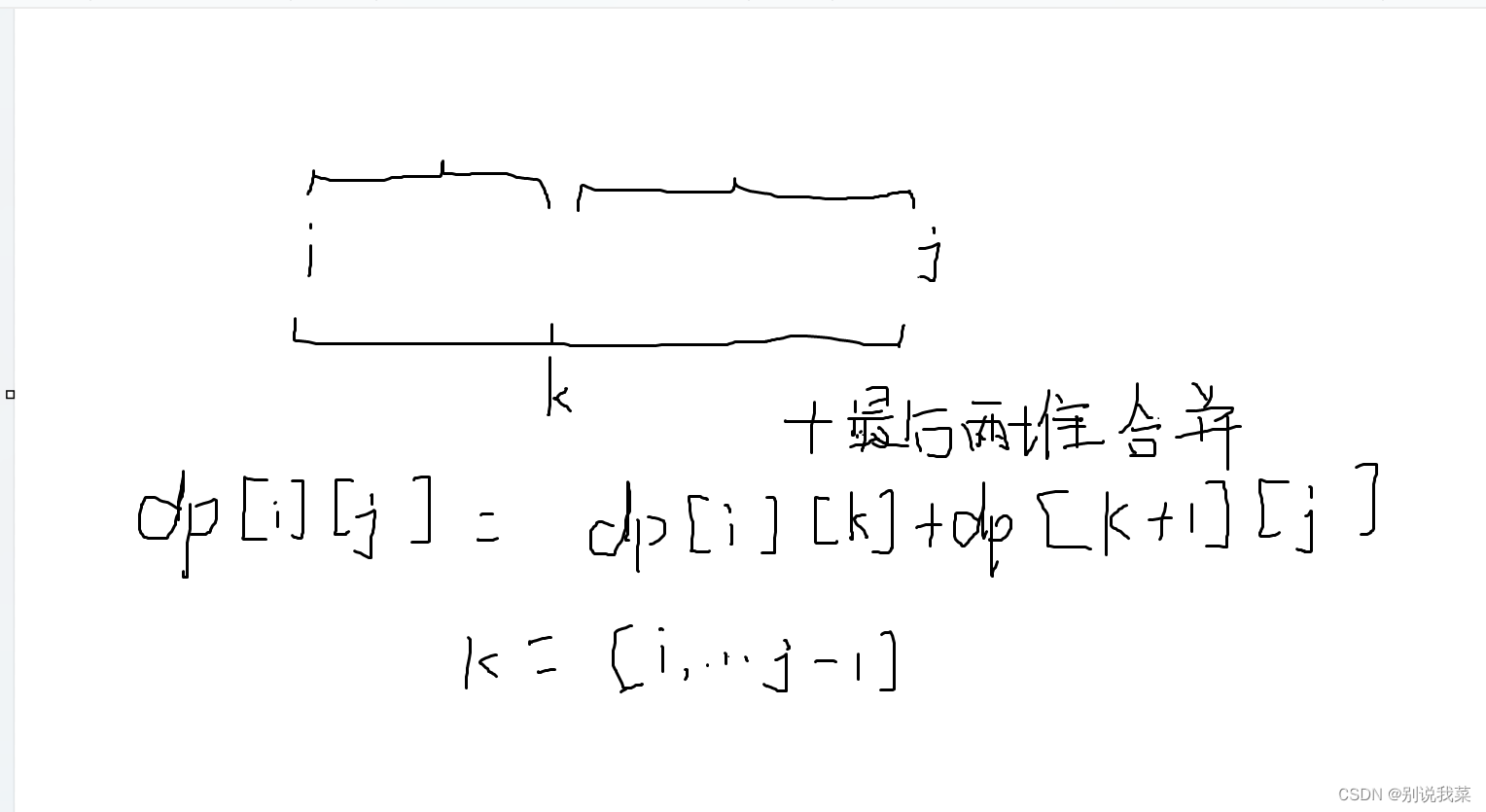
 图1.1思路模拟

 我们可以通过枚举区间长度len，从1枚举n，当然区间长度为1的时候，说明只有一堆石子，就不要合并，代价为0。

然后我们在从1开始枚举左区间的起始端点i，i的值从1枚举到n。我们知道区间长度len，知道左端点i，那么我们就可以得到区间的右端点j=i+len-1。

此时我们再枚举中间端点k，k的值的话从i枚举到j-1，因为我们最后用k将区间分成两堆，分别是i到k堆和k+1到j堆，那么我们k的取值就是从i到j-1。

那么dp[i][j]的值就是从第i堆到第k堆的最小代价数加上第k+1堆到第j堆的最小代价数再加上最后两堆的代价数，我们通过观察可以发现最后两堆的合并一定是第i堆到k堆的连续合并和后面从第k+1堆到第j堆的连续合并之和，那么最后一次就相当于求区间和，我们可以通过前缀和数组的方法来进行处理。

2.状态递推公式

当i=j时，即就一堆：

当 枚举中间端点k时：

 

注：其中一维数组s表示石子质量的前缀和数组，故求第i堆到第j堆石子重量的和为

        

dp数组构建代码如下：

        //区间长度
        for(int len = 2; len <= n;len++){
            //枚举左端端点
            for(int i = 1; i + len - 1 <= n;i++){
                //最右端端点
                int j = i + len -1;
                //初始化
                dp[i][j] = Integer.MAX_VALUE;mei
                //左右端点相等，那么就一堆，不需要进行操作
                if(i == j){
                    dp[i][j] = 0;
                }
                //枚举中间端点
                for(int k = i; k <= j-1;k++){
                    dp[i][j] = Math.min(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);
                }
            }
        }

二、代码如下

代码如下（示例）：

import java.io.*;
import java.util.ArrayList;
import java.util.Scanner;

public class 石子合并 {
    static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    public static void main(String[] args) {
        Scanner  sc = new Scanner(new BufferedReader(new InputStreamReader(System.in)));
        int n = sc.nextInt();
        int[] s = new int[310];
        int[][] dp = new int[310][310];
        for(int i = 1; i <= n;i++){
            s[i] = sc.nextInt();
        }
        for(int i = 1;i <= n;i++){
            s[i] = s[i]+s[i-1];
        }
        //区间长度
        for(int len = 2; len <= n;len++){
            //枚举左端端点
            for(int i = 1; i + len - 1 <= n;i++){
                //最右端端点
                int j = i + len -1;
                //初始化
                dp[i][j] = Integer.MAX_VALUE;
                //左右端点相等，那么就一堆，不需要进行操作
                if(i == j){
                    dp[i][j] = 0;
                }
                //枚举中间端点
                for(int k = i; k <= j-1;k++){
                    dp[i][j] = Math.min(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);
                }
             }
        }
        pw.println(dp[1][n]);
        pw.flush();
    }
}

2.读入数据

代码如下（示例）：

4
1 3 5 2

3.代码运行结果如下：

22

---

总结

石子合并问题是经典的区间dp问题，我们需要枚举中间端点k的情况从而来推出dp数组的值。