想借着这一个题回顾一下动态规划问题的基本解法,让解题方法清晰有条理,希望更多的人可以更轻松的理解动态规划!
目录
【题目】
【本题解题思路】
【DP模版】
总体方针:
具体解题时的套路:
【题目】
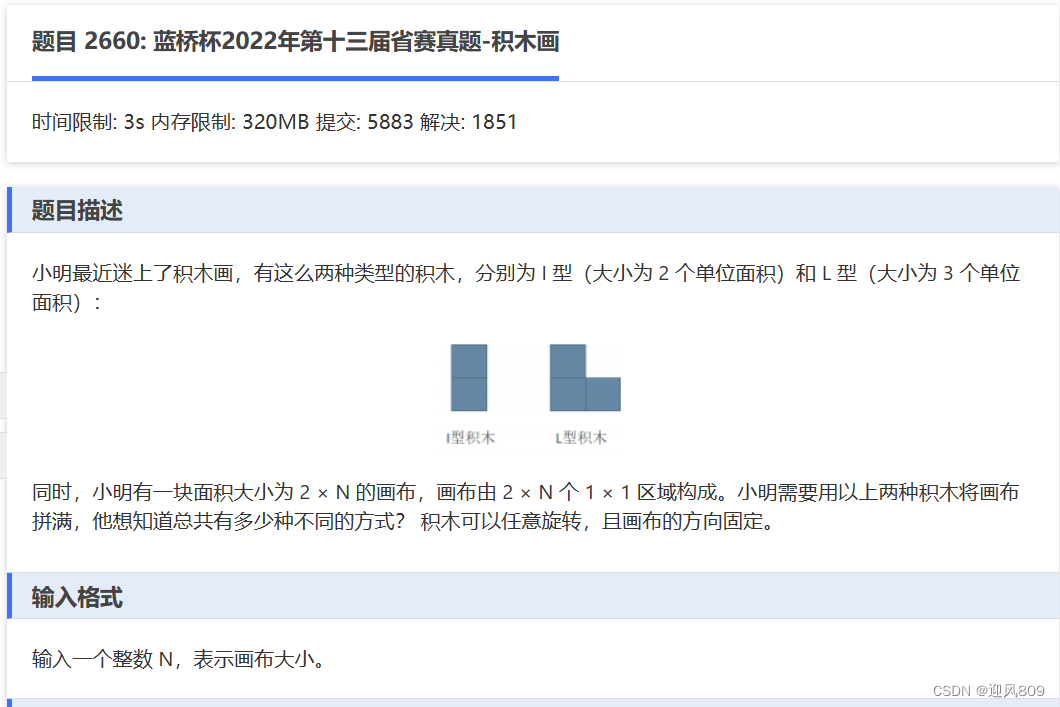
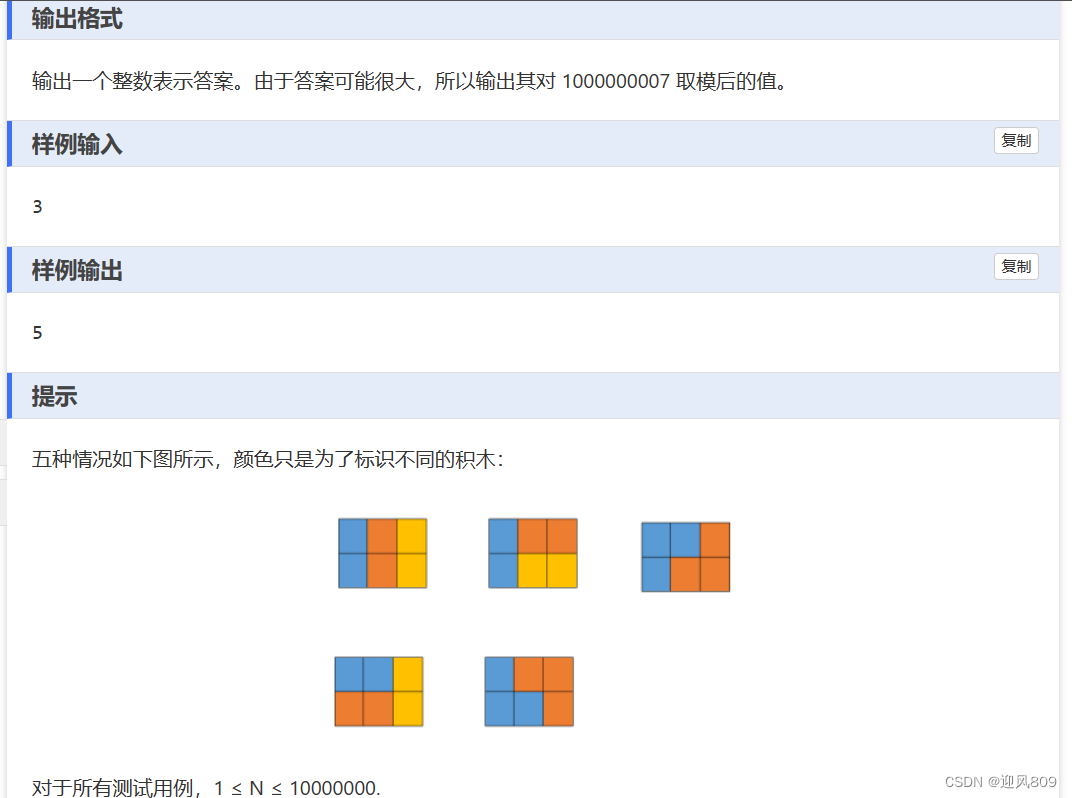
【本题解题思路】
———类似题目:覆盖墙壁 - 洛谷(很多经典题解在里面)
1、确定子状态:
我最终要求解的是:用两种类型的积木将2 x n的画卷填满时有着多少种组合方案。(围绕最终要求解的问题确定子问题)
所以子问题应该是在长度为n的情况下有多少种解法。
所以用一维数组dp[i] 存储长度为i 时的方案数。
2、确定转移的边界情况和初始状态:
这里先正着推,已知n=3时dp[3]=5,那么就可以先明确n=1,n=2时对应的dp[i],即dp[1]=1,dp[2]=2;
然后发现没有什么明显的规律呢,那就再倒着来
3、确定状态转移方式:
为了方便表述,设画卷长度为len;
我想知道画卷长度为len=n时的值,那么我就找他的上一层 len=n-1时的状态,看看有没有什么关联。为了形成填满画卷的状态,我的最后一块位置可以怎么摆放积木呢,从积木的两种类型出发,发现他可以形成四种状态。这里用分类的思想将所有的选择罗列出来,找规律。
如图所示,最后一次有如下选择:
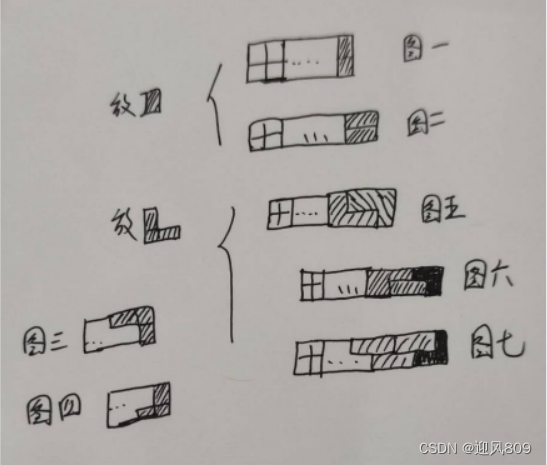
(1)最后一次选竖着的I ,那么dp[n]=dp[n-1]。
因为最后一位固定好了就这一种选择,即1*dp[n-1]。如图1;
(2)最后一次选横着的I ,那么为了填补上画卷,第二行也只能选横着的I 这两个横着的I作为一个整体是一种填补画卷的方式。此时dp[n]=dp[n-2];
如图2所示。
前两种状态都很明显,但是如果选用L形的怎么罗列呢:
(3)L型垂直翻转前后算两种状态,如图3、4. 下面仅根据其中的一种情况来讨论,最后因为翻转所有的结果×2 即可。
A.可以用两个L形成长度为3的整体来填补画卷,dp[n]=dp[n-3],如图5;
B.采用两个L和一个横着的I的方式形成一个整体作为一种方法填补,dp[n]=dp[n-4],如图6;
C.同上,还可以采用在两侧两个L中间包裹多个横着的I的方式来填补,每多一个横着的I相当于这个用于填补的图像整体的长度+1。所以类推得到dp[n]=dp[n-5],dp[n-6],... 如图7;
综上所述,形成填满画卷的前一个整体的状态可以采用如上这些方式,所以他的方案总数就有:
dp[n]=dp[n-1]+dp[n-2]+2*(dp[n-3]+dp[n-4]+...dp[0]);
假如用前缀和sum[n]表示前n个长度的方案总和,dp[n]=sum[n-1]+sum[n-3];
但是我这里只求了n=1---3的情况,n=4时情况虽然有点复杂,但是也还是不好求(哈哈)。
所以有没有什么化简的方式呢,大家记不记得高考时第一个大题考的数组的性质,这里就可以用来变换公式;
dp[n]=sum[n-1]+sum[n-3];
dp[n-1]=sum[n-2]+sum[n-4];
上下相减发现 dp[n]-dp[n-1]=dp[n-1]+dp[n-3];
所以,dp[n]=2*dp[n-1]+dp[n-3]
这就把递推公式推出来了,完美撒花!
【DP模版】
总体方针:
凡是动态规划问题,可以从以下三个角度考虑,确定求解问题的基本思路:
(有时是二维问题或者多维问题时可以考虑用二维或者多维数组)

动态规划问题具有两个性质:
(1)无后效性:每个子问题的解都是基于之前子问题的解,而不受后续子问题解的影响。这意味着我们可以独立地解决每个子问题,然后将这些解组合起来形成一个最优解。即当前状态的解只受此状态之前(就是过去的状态)的影响,一经确定,未来的状态不影响当前状态的结果。
(换成人话就是,当前状态的结果是由之前状态形成的,一旦确定,后续的状态对他没有影响)
(2)子问题重叠性:每个子问题之间类似于嵌套的关系,我想求这个子问题,就必须先解决比他规模更小的、具有同样规律的子问题。
具体解题时的套路:
1、按照题目的求解问题,确定子问题是什么,把存储每个子问题的数据结构定义出来;
2、根据题目中给的信息,自己推理、枚举出来所有的可以获得的关于解的信息,看看是否存在什么规律。这里推倒的方式往往是从边界开始往前推导,观察前后状态之间的联系。或者是从初始状态向后推导,找规律。