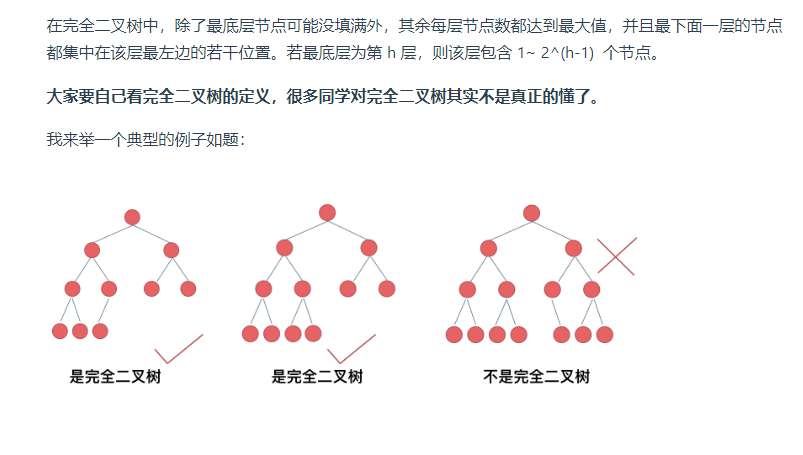
233的字符串

题目描述

读入一个正整数n，代表将字符串"abc"重复n次，形成一个长度为3n的字符串。

例如n=3时，形成的字符串为"abcabcabc"。

请你计算该字符串中有多少个"acb"子序列。答案对10^9+7取模。

输入描述:

一个正整数nn

1<=n<=1e9.

输出描述:

"acb"子序列的数量。答案对10^9+7取模。

示例1

输入

复制

3

输出

复制

4

说明

abcabcabc

abcabcabc

abcabcabc

abcabcabc

如上，四个子序列的位置已标记。

思路：

不难发现的是，如果把每个abc当做一个位置，那么acb要么分别位于三个位置，要么ac在一个位置，b在一个位置，所以答案为C(n,3)+C(n,2)，是一个阶乘级别的数。

如果直接去算的话，非常不好算，因为有阶乘，用高中的数学知识可以求出：

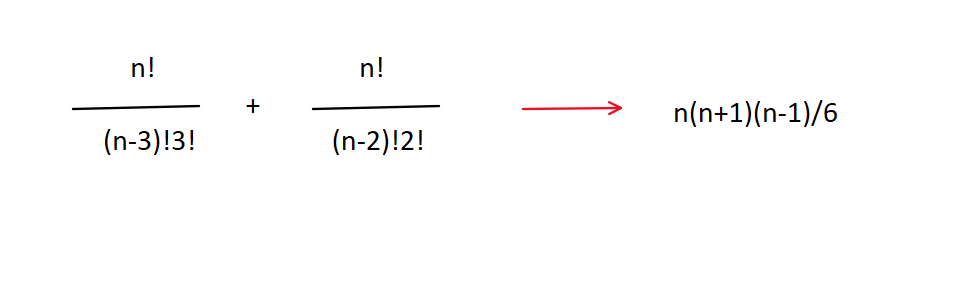
如果这就完了的话，那真的是小看这一题了。

看似简单，实际上有一个很大的坑！

因为再求解的过程中，如果每一步不先模1e9+7的话，会导致数据溢出，因为题目中的数据n是1e9,加上结果相当于n的3次方，是一个很大的数，肯定会爆long long,这时候就需要把式子进行拆开求解，拆成两个数相乘，每个数分别先模1e9+7,然后相乘。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long ll;
const ll M=1e9+7;
ll n,ans;
int main()
{
    cin>>n;
    ans=((n*(n-1)/2)%M*(n+1)/3)%M;
    cout<<ans<<endl;
    return 0;
}

牛客真的是有坑。