【Day2】977有序数组的平方、209长度最小的子数组、59螺旋矩阵Ⅱ
- 977有序数组的平方
- 暴力排序
- 双指针法
- 209长度最小的子数组
- 暴力解法
- 滑动窗口法
- 59螺旋矩阵Ⅱ
977有序数组的平方
题目链接:977
题目:给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
暴力排序
每个数平方之后,排序。
class Solution {
public:
vector<int> sortedSquares(vector<int>& A) {
for(int i=0;i<A.size();i++){
A[i]*=A[i];
}
sort(A.begin(),A.end());//快速排序
return A;
}
};
//时间复杂度是 O(n + nlogn)
双指针法
数组是有序的,负数平方后会变大,那么数组平方后的新数组中的最大值可能就在最左端或最右端,不会在中间(数组是有序的),考虑双指针法,i指向起始位置,j指向终止位置。
定义一个新数组result,和A数组一样的大小,让k指向result数组终止位置。
如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。
如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。
class Solution {
public:
vector<int> sortedSquares(vector<int>& A) {
int k=A.size()-1; //k是新数组的下标
vector<int> result(A.size(), 0);
for(int i=0,j=A.size()-1;i<=j;){
if(A[i]*A[i]<A[j]*A[j]){
result[k--]=A[j]*A[j];
j--;
}else{
result[k--]=A[i]*A[i];
i++;
}
}
return result;
}
};
//时间复杂度为O(n)
209长度最小的子数组
题目链接:209
题目:
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
暴力解法
两个for循环,一个for循环是区间的起始位置,一个for循环是区间的终止位置,然后不断的寻找符合条件的子序列,时间复杂度很明显是O(n^2)。
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int result = INT32_MAX; // 最终的结果
int sum = 0; // 子序列的数值之和
int subLength = 0; // 子序列的长度
for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
sum = 0;
for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
sum += nums[j];
if (sum >= s) { // 一旦发现子序列和超过了s,更新result
subLength = j - i + 1; // 取子序列的长度
result = result < subLength ? result : subLength;
break; // 因为我们是找符合条件最短的子序列,所以一旦符合条件就break
}
}
}
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == INT32_MAX ? 0 : result;
}
};
//时间复杂度:O(n^2)
//空间复杂度:O(1)
滑动窗口法
滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
滑动窗口只用一个for循环,循环的索引是滑动窗口的终止位置。
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int result=INT32_MAX;
int sum=0; //滑动窗口数值之和
int i=0; //滑动窗口起始位置
int subLength=0; //滑动窗口的长度
for(int j=0;j<nums.size();j++){
sum+=nums[j];
while( sum >= target){
subLength = (j-i+1); //新数组的长度
result = result < subLength ? result : subLength;
sum -= nums[i++]; //初始下标i向后移,sum减去前面i的值
}
}
return result == INT32_MAX ? 0 : result;
}
};
//时间复杂度:O(n)
//空间复杂度:O(1)
【注意】INT32_MAX
//INT_MAX是一个很大的数,
INT32_MAX=2^31-1
INT32_MIN=-2^31
59螺旋矩阵Ⅱ
【面试高频题】
题目链接:59
题目:
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
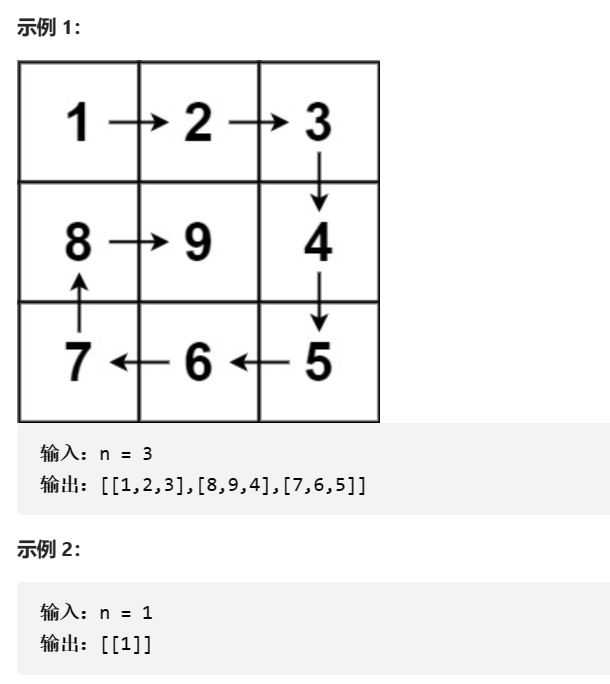
求解本题要坚持循环不变量原则。
模拟顺时针画矩阵的过程:
填充上行从左到右
填充右列从上到下
填充下行从右到左
填充左列从下到上
由外向内一圈一圈这么画下去。
每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
视频讲解:59螺旋矩阵
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定义一个二维数组
int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
int loop = n / 2; // 每个圈循环几次,例如n为奇数3,那么loop = 1 只是循环一圈,矩阵中间的值需要单独处理
int mid = n / 2; // 矩阵中间的位置,例如:n为3, 中间的位置就是(1,1),n为5,中间位置为(2, 2)
int count = 1; // 用来给矩阵中每一个空格赋值
int offset = 1; // 需要控制每一条边遍历的长度,每次循环右边界收缩一位
int i,j;
while (loop --) {
i = startx;
j = starty;
// 下面开始的四个for就是模拟转了一圈
// 模拟填充上行从左到右(左闭右开)
for (j = starty; j < n - offset; j++) {
res[startx][j] = count++;
}
// 模拟填充右列从上到下(左闭右开)
for (i = startx; i < n - offset; i++) {
res[i][j] = count++;
}
// 模拟填充下行从右到左(左闭右开)
for (; j > starty; j--) {
res[i][j] = count++;
}
// 模拟填充左列从下到上(左闭右开)
for (; i > startx; i--) {
res[i][j] = count++;
}
// 第二圈开始的时候,起始位置要各自加1, 例如:第一圈起始位置是(0, 0),第二圈起始位置是(1, 1)
startx++;
starty++;
// offset 控制每一圈里每一条边遍历的长度
offset += 1;
}
// 如果n为奇数的话,需要单独给矩阵最中间的位置赋值
if (n % 2) {
res[mid][mid] = count;
}
return res;
}
};```