LeetCode 热题 100 | 多维动态规划（二）

news2024/12/23 7:39:31

1 5. 最长回文子串

2 1143. 最长公共子序列

菜鸟做题，语言是 C++

1 5. 最长回文子串

核心思想：把总问题拆解为若干子问题。

总问题：从第 i 个字母到第 j 个字母是回文串
子问题：从第 i + 1 个字母到第 j - 1 个字母是回文串、第 i 个字母等于第 j 个字母
总问题 = 子问题 1 + 子问题 2

思路说明图：如下图所示，要使 “从第 i 个字母到第 j 个字母是回文串”，必须满足 “从第 i + 1 个字母到第 j - 1 个字母是回文串” 和 “第 i 个字母等于第 j 个字母” 这两个条件。

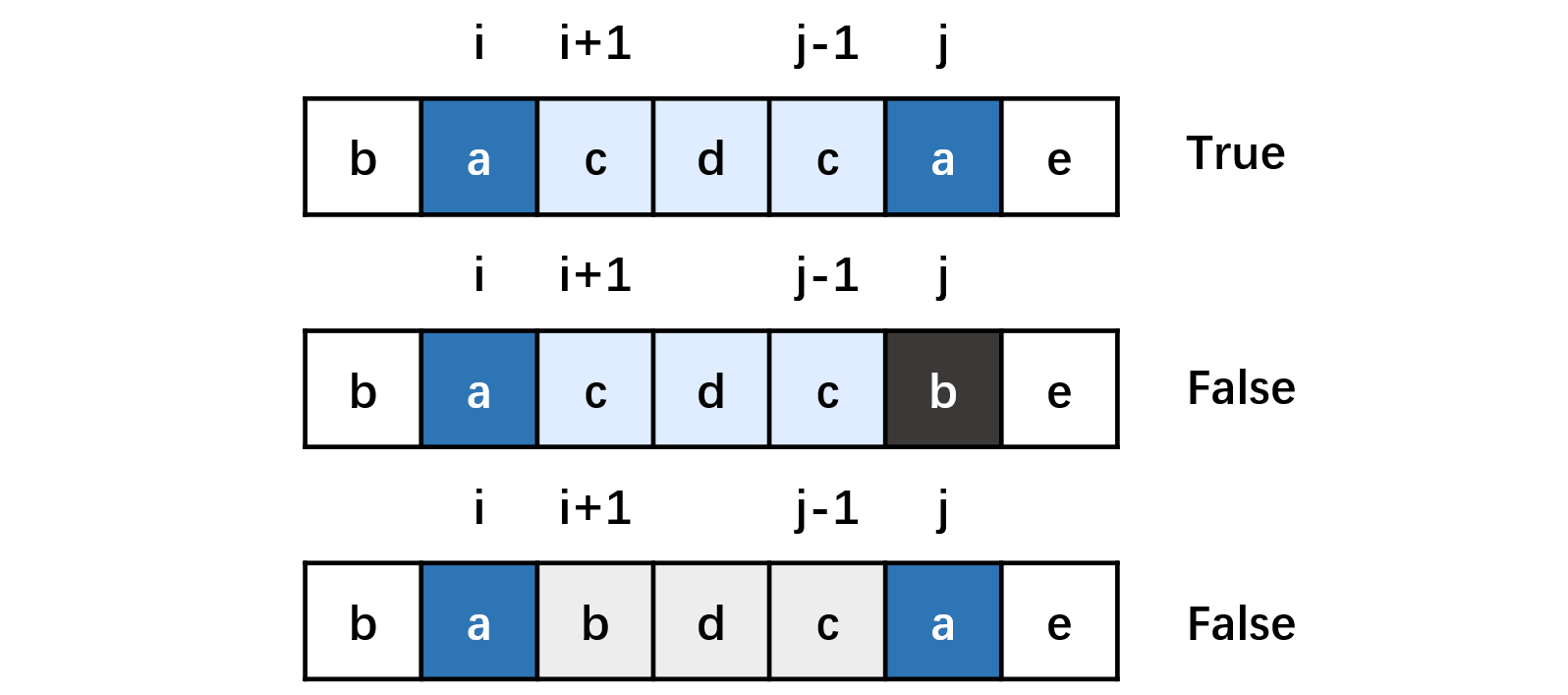
很自然地想到设置一个 dp 二维数组，其中的 dp[i][j] 用于记录 “从第 i 个字母到第 j 个字母” 是否是回文串。如果是，则 dp[i][j] = 1；否则，dp[i][j] = 0 。

最初可能会想到这样写循环：

for (int i = 0; i < n; ++i) {
    for (int j = i; j < n; ++j) {
        dp[i][j] = dp[i + 1][j - 1] && s[i] == s[j];
    }
}

但问题在于，当我们计算 dp[i][j] 的时候，dp[i + 1][j - 1] 还没有被算出来。

因此，我们把 “从前往后” 遍历改为 “从后往前” 遍历：

for (int i = n - 1; i >= 0; ++i) {
    for (int j = i; j < n; ++j) {
        dp[i][j] = dp[i + 1][j - 1] && s[i] == s[j];
    }
}

由于 i = n - 1 会导致 dp[i + 1][j - 1] 访问越界，因此我们还会加入一些判断条件。

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        if (n < 2) return s;

        vector<vector<int>> dp(n, vector<int>(n, 0));
        string ans;
        for (int i = n - 1; i >= 0; --i) {
            for (int j = i; j < n; ++j) {
                if (i + 1 <= j - 1) {
                    dp[i][j] = dp[i + 1][j - 1] && s[i] == s[j];
                } else {
                    dp[i][j] = s[i] == s[j];
                }
                
                if (dp[i][j] && s.substr(i, j - i + 1).size() > ans.size())
                    ans = s.substr(i, j - i + 1);
            }
        }

        return ans;
    }
};

说明：if (i + 1 <= j - 1) 是在判断什么？

上图给出了 “i 和 j 之间没有夹子串” 的两种情况，我们直接判断 s[i] 和 s[j] 是否相等即可。

2 1143. 最长公共子序列

核心思想：把总问题拆解为若干子问题。

总问题：text1 前 i 个字母和 text2 前 j 个字母有多少个相同
子问题：text1 前 i/i-1 个字母和 text2 前 j-1/j 个字母有多少个相同
总问题 = 子问题 1 + 子问题 2

思路说明图：设置一个 dp 二维数组，其中 dp[i][j] 代表 text1 前 i 个字母和 text2 前 j 个字母的相同个数。假设 text1[i] 和 text2[j] 不同，那么 dp[i][j] 只能从 dp[i][j - 1] 和 dp[i - 1][j] 中继承一个，由于是在求最长，因此继承二者中的较大者。

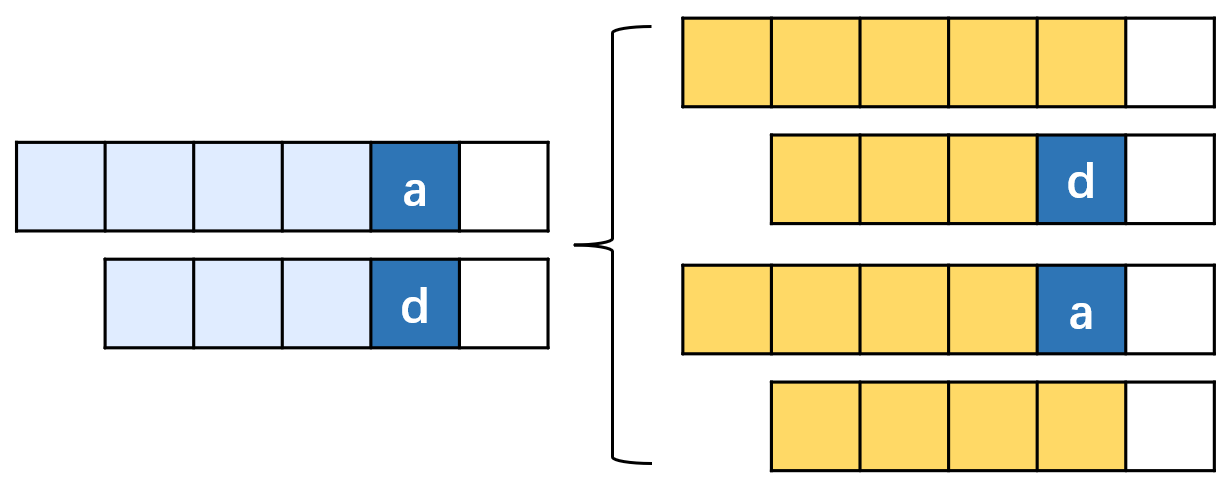
如果 text1[i] 和 text2[j] 相同，则 dp[i][j] = dp[i - 1][j - 1] + 1，而不能从 dp[i][j - 1] 和 dp[i - 1][j] 中继承，否则会导致 text1[i] 或 text2[j] 被重复使用。

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m = text1.size();
        int n = text2.size();

        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (text1[i - 1] == text2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
                }
            }
        }

        return dp[m][n];
    }
};