💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤
📃个人主页 ：阿然成长日记 👈点击可跳转
📆 个人专栏： 🔹数据结构与算法🔹C语言进阶🔹C++
🚩 不能则学，不知则问，耻于问人，决无长进
🍭 🍯 🍎 🍏 🍊 🍋 🍒 🍇 🍉 🍓 🍑 🍈 🍌 🍐 🍍

一、问题引入

看下幅图：执行了四次make，有时会执行依赖方法，重新编译了，有时又不会变化。

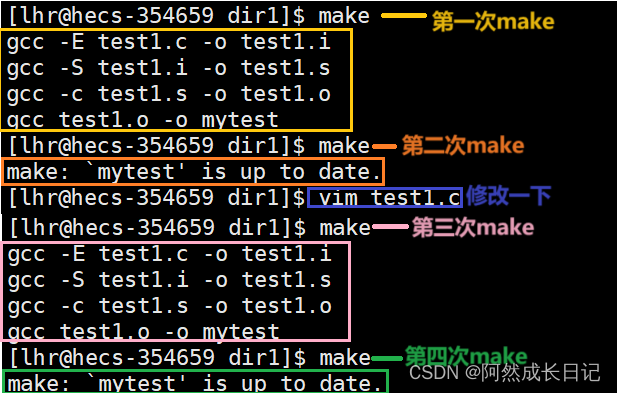
首先我们应该清楚，make的这种机制是很好的，因为每编译一次，都会消耗资源与时间。所以，如果依赖文件内容如果没有发生变化的话，就应该保留上次的编译结果，不在重复执行，增加消耗。

二、ACM时间

首先，了解一下ACM时间是什么：
每一个文件都会有它的ACM时间，去记录它的时间信息。

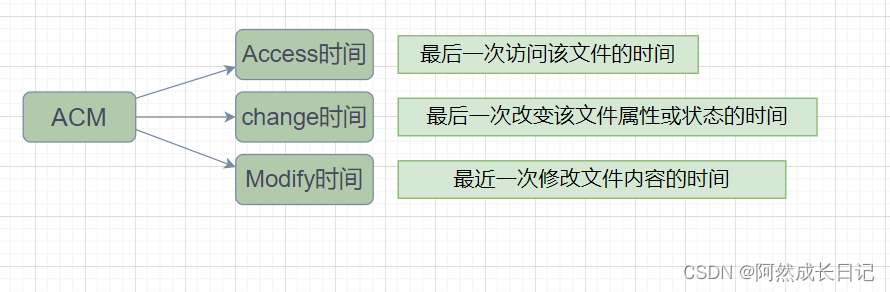
make指令通过这个Modify时间来进行对比才能判断出是否需要重新编译。

三、make如何判断的呢？

演示一下：

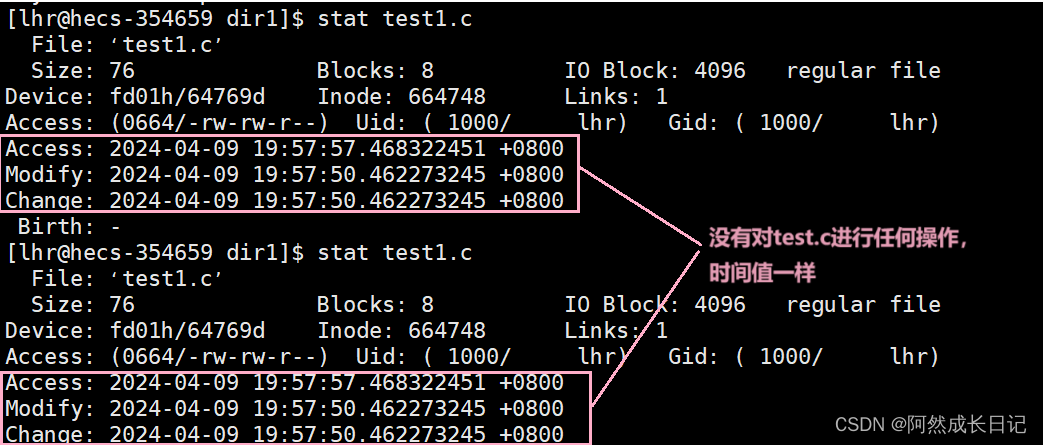
此时使用make就会，显示make: `mytest’ is up to date.。不会重新编译。

接下来，修改一下test1.c.

1.只是进行cat查看，修改了Access时间。不重新编译。

2.使用vim修改。改动了Modify时间。重新编译。

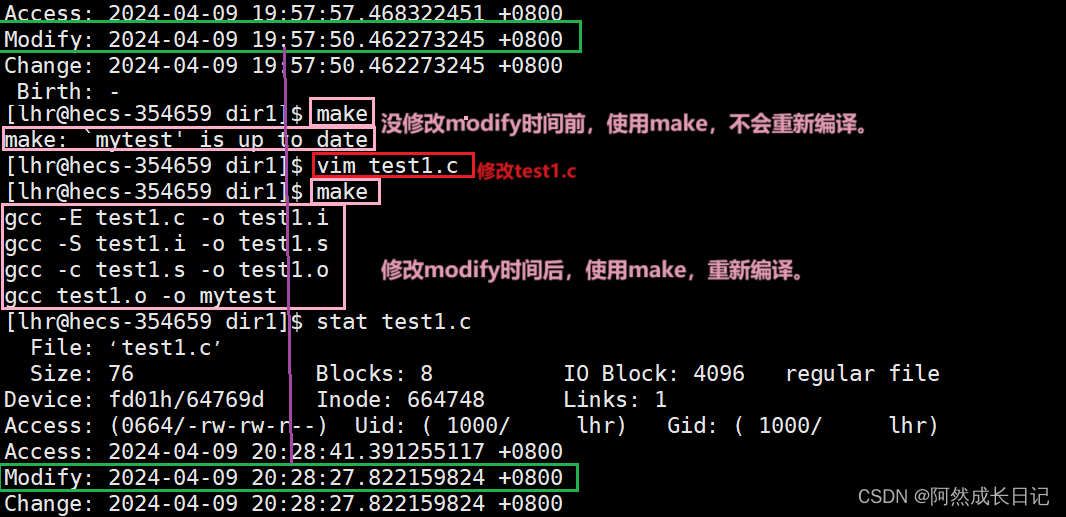
四、总结

make是根据【modify时间是否变化】判断可执行文件是否需要重新编译。