前言
大家好,我是jiantaoyab,开始刷动态规划的回文串类型相关的题目
动态规划5个步骤
- 状态表示 :dp数组中每一个下标对应值的含义是什么>dp[i]表示什么
- 状态转移方程: dp[i] 等于什么
- 1 和 2 是动态规划的核心步骤,第三步是初始化,保证填表的时候不越界
- 填表顺序:为了保证填写当前状态的时候,所需要的状态已经计算过
- 返回值
回文子串

题目分析
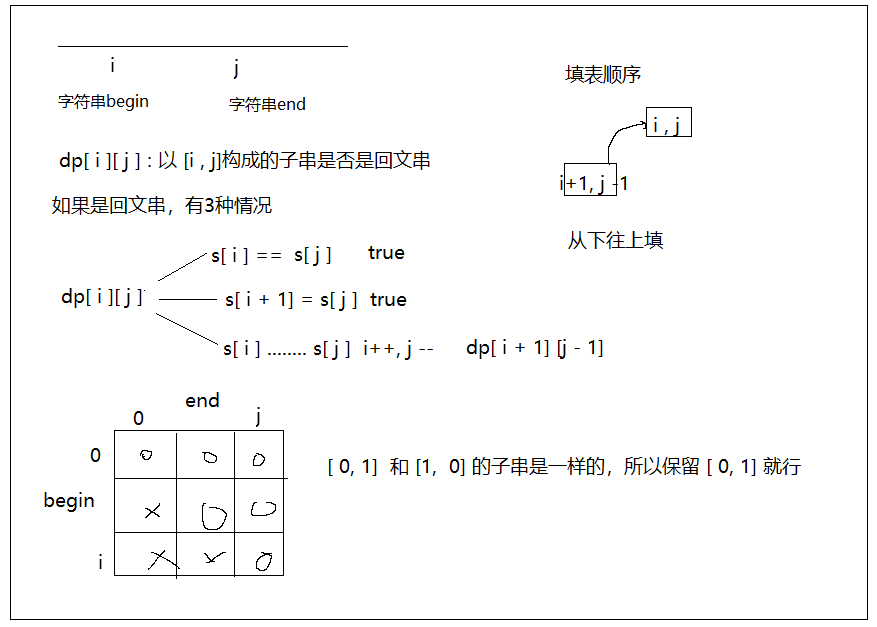
代码
class Solution {
public:
int countSubstrings(string s) {
int n = s.size();
int ret = 0;
vector<vector<bool>> dp(n, vector<bool>(n));
for(int i = n - 1; i >= 0; i--)
{
for(int j = i; j < n; j++) // i <= j
{
if(s[i] == s[j])
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
if(dp[i][j]) ret++;
}
}
return ret;
}
};
最长回文子串

代码
动态规划版本
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n));
int len = 1, begin = 0;
for(int i = n - 1; i >= 0; i--)
{
for(int j = i; j < n; j++)
{
if(s[i] == s[j]) dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
if(dp[i][j] && j - i + 1 > len)
{
len = j - i + 1;
begin = i;
}
}
}
return s.substr(begin, len);
}
};
中心探测法

class Solution {
public:
string longestPalindrome(string s) {
string RetStr="";
for(int i=0;i<s.size();i++)
{
//回文串为奇数
int left=i-1;
int right=i+1;
while(left>=0&&right<s.size()&&s[left]==s[right])
{
left--;
right++;
}
if(RetStr.size()<right-left-1)
{
//babad
//01234 letf=-1 i=1 right=3
RetStr=s.substr(left+1,right-left-1);
}
//回文串为偶数
left=i;
right=i+1;
while(left>=0&&right<s.size()&&s[left]==s[right])
{
left--;
right++;
}
if(RetStr.size()<right-left-1)
{
RetStr=s.substr(left+1,right-left-1);
}
}
return RetStr;
}
};
分割回文串 IV

代码
class Solution {
public:
bool checkPartitioning(string s) {
int n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n));
int count = 0;
for(int i = n - 1; i>= 0; i--)
{
for(int j = i; j < n; j++)
{
if(s[i] == s[j] ) dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
}
}
//枚举第二个字符串的起始位置和结束位置
for(int i = 1; i < n - 1; i++) //前后留一个字符给第一个字符串
{
for(int j = i; j < n - 1; j++)//结束位置从i开始到n - 1
{
if(dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1] ) return true;
}
}
return false;
}
};
分割回文串 II

题目分析

代码
class Solution {
public:
int minCut(string s) {
int n = s.size();
vector<vector<bool>> is_pal(n, vector<bool>(n));
int ret = 0;
//把所有子串是不是回文串放到is_pal中
for(int i = n - 1; i >= 0; i--)
{
for(int j = i; j < n; j++)
{
if(s[i] == s[j]) is_pal[i][j] = i + 1 < j ? is_pal[i + 1][j - 1] : true;
}
}
vector<int> dp(n, INT_MAX);
for(int i = 0; i < n; i++)
{
if(is_pal[0][i]) dp[i] = 0;
// [0, i] 不是回文串
else
{
for(int j = 1; j <= i; j++)
{
if(is_pal[j][i]) dp[i] = min(dp[i], dp[j - 1] + 1);
}
}
}
return dp[n - 1];
}
};
最长回文子序列

题目分析

代码
class Solution {
public:
int longestPalindromeSubseq(string s) {
int n = s.size();
vector<vector<int>> dp(n, vector<int>(n));
//填表从下到上,左到右填
for(int i = n - 1; i >= 0; i--)
{
dp[i][i] = 1; // i == j
for(int j = i + 1; j < n; j++)
{
if(s[i] == s[j])
{
if(i + 1 == j) dp[i][j] = 2;
else if(i + 1 < j) dp[i][j] = dp[i + 1][j - 1] + 2;
}
else
{
dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]);
}
}
}
return dp[0][n - 1];
}
};
让字符串成为回文串的最少插入次数

题目分析

class Solution {
public:
int minInsertions(string s) {
int n = s.size();
vector<vector<int>> dp(n, vector<int>(n));
for(int i = n - 1; i >=0; i--)
{
for(int j = i + 1; j < n; j++)
{
if(s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1];
else
{
dp[i][j] = min(dp[i + 1][j] + 1, dp[i][j - 1] + 1);
}
}
}
return dp[0][n - 1];
}
};