参数估计是推断统计的重要内容之一。它是在抽样及抽样分布的基础上，根据样本统计量来推断所关心的总体参数。说白了，就是用样本信息来代替总体信息

• 例如：现在要调查某大学大学生的一个消费情况，假设全校大学生的平均消费金额为$\mu$，那么我们随机抽取一个样本，这个样本的平均消费水平为$\overline{x}$，理论上，可以用$\overline{x}$代替$\mu$。
    参数估计主要分为点估计和区间估计。下面就讲一下这两种估计。

1.点估计

  点估计——用样本的估计量的某个取值直接作为总体参数的估计值

• 例如：用样本均值直接作为总体均值的估计；用两个样本均值之差直接作为总体均值之差的估计

**注意：**点估计无法给出估计值接近总体参数程度的信息
由于样本是随机的，抽出一个具体的样本得到的估计值很可能不同于总体真值。一个点估计量的可靠性是由它的标准误来衡量的，这表明一个具体的点估计值无法给出估计的可靠性的度量。

1.1 矩估计

  用样本的K阶原点矩替代总体的K阶原点矩, 这样得到的未知参数θ的估计量称为θ的矩估计量

具体步骤如下：

• 就是用${\mu }_k=A_k$，题目有n个未知参数，就列出n个等式，就可以了，再根据方程解出未知参数。

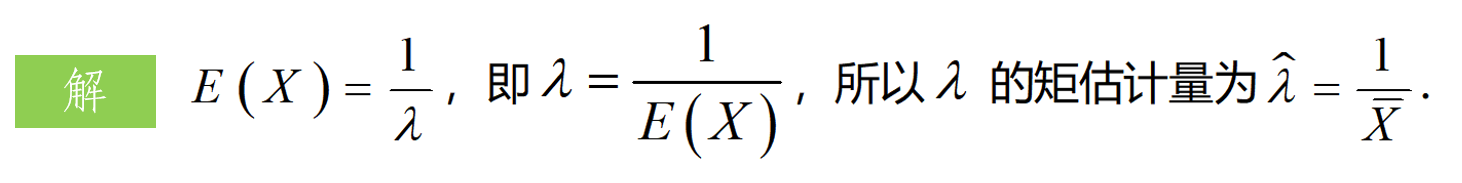
1.2 极大似然估计

  有些教材称为最大似然估计，说白了，就是依据最大的概率进行估计。

  很明显，白球应该有99个，黑球只有1个。若白球只有1个，那么白球在一次抽取中被抽中的概率是0.01，那么连续两次抽中白球的概率是$0.01^2$,这个概率很小，是一个小概率事件。一般来说，小概率事件不可能在一次事件中发生的。所以，就认为黑球只有1个。

注意:
  (1)似然函数就是这个样本被抽中的概率，由于各个样本是独立的，所以联合概率就等于各个概率相乘；
  (2)既然这个样本被抽中了，就说明这个样本被抽中的概率很大，例如，我从A班抽中了一个人的分数在（60，70）之间，就说明这个班（60，70）段的人数很多，我才能在这次抽样中抽中；
  (3)我们只关心使得这个似然函数取得极大值的极大值点（也就是待估计参数）的取值，不管这个极大的概率具体是多少，所以可以取对数，因为取对数不改变原函数极大值点的位置。

对于评价估计量的标准中的无偏性、有效性和相合性，经常考的是无偏性和有效性。因为由点估计可知，一个参数的点估计量有很多个，那么选择哪个估计量就是我们要考虑的事情了。这里首要考虑无偏性，再就是有效性了。

1.3 评价估计量的标准

1.3.1 无偏性

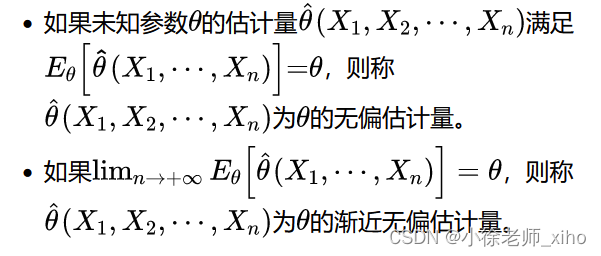
无偏性——估计量抽样分布的数学期望等于被估计的总体参数

1.3.3 有效性

有效性——对同一总体参数的两个无偏点估计量，标准差小的估计量更有效

1.3.2 相合性

相合性（一致性）——随着样本量的增大，估计量的值越来越接近被估计的总体参数

• 例如，总体有100个，我取的样本量依次为1,3,6,20,50,60，那么这个样本量增大就会导致这个样本均值越来越进行总体均值。