贪心算法的理论基础
主要的思路就是通过想局部最优解然后看能不能推导出全局最优,但是贪心算法没有统一的套路,每一个问题的贪心思路都可以非常不一样
Leetcode 455. 分发饼干
讲解前:
这时第一道贪心算法的题目,所以很简单,然后我也没有想太多莫名其妙的就写出来了,大致思路就是孩子的数量是这道题的首要目标,那么为了能让更多的孩子满足,我们要避免浪费饼干的情况,也就是说如果有孩子1,3和饼干1,3,我们不能把3喂给1,导致孩子3只剩下饼干1不能饱,最合理的思路就是尽可能的把小饼干给小孩子,所以我就把饼干和孩子都从大到小排序了之后然后一个一个对比,能给就给
class Solution:
def findContentChildren(self, g: List[int], s: List[int]) -> int:
g.sort()
s.sort()
res = 0
i = 0
for cookie in s:
if i < len(g) and cookie >= g[i]:
res = res + 1
i = i + 1
return res讲解后:
卡哥的思路和我的一样,并且我觉得我这个思路其实更好理解一点,通过用小饼干满足小的小孩,这样不用嵌套for和while循环
Leetcode 376. 摆动序列
讲解前:
完全没什么思路,感觉这道题好难,子序列可以不用连续,而且还有多个需要找
讲解后:
这道题的关键其实就在于理解透彻贪心的点,因为你会发现当你写代码的时候,这道题就好像是一个普通的通过一次遍历就能解决的问题,不容易看出我们的局部解是什么,其实这道题的核心思路是,如果要找到一个从一个数组中找一个最长的子序列并且保证都是摆动序列,可以反过来想
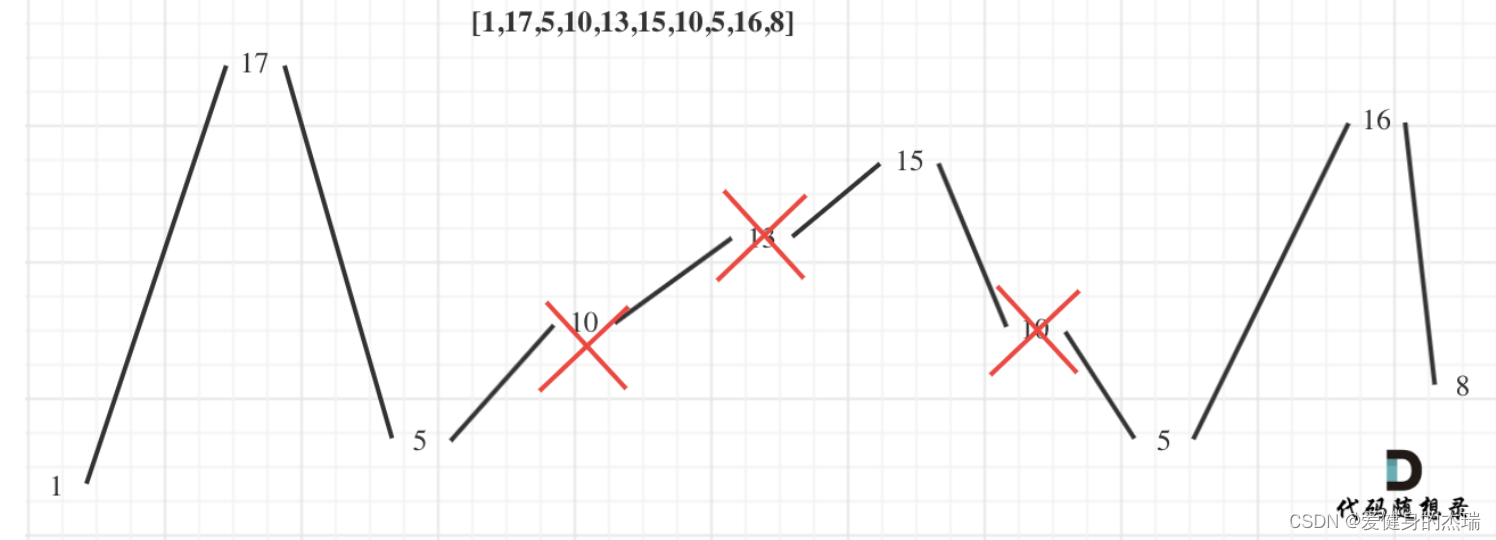
摆动序列把图画出来,你会发现每一个峰值的点都是一个可以加入到摇摆序列中的数字,那我们贪心贪的就应该是这些峰值的值,局部的最优解就是但凡我们当前的数字满足作为一个峰值的条件,那么我们就应该把他算上,然后呢只要我们确保了没有落下一个峰值,在遍历整个数组的情况下,就能收集到最长的摇摆序列
class Solution:
def wiggleMaxLength(self, nums: List[int]) -> int:
res = 1
pre_diff = 0
for i in range(0, len(nums) - 1):
cur_diff = nums[i + 1] - nums[i]
if (cur_diff > 0 and pre_diff <= 0) or (cur_diff < 0 and pre_diff >= 0):
res = res + 1
pre_diff = cur_diff
return res这里为了方便我们的代码不用处理edge case,做两个处理,第一就是把pre_diff先设成0,这样从第一个数字遍历的时候我们可以确保res会加1,然后把res一开始就初始化为1可以确保最后一个数字也会直接算加入到了res中,因为题目说了只有一个元素或者只有两个不等的元素也算作摇摆序列,这里还需要注意的是我们的pre_diff只需要在我们发现了一个新的要加入摇摆序列的值的时候再更新到旧的那里去避免出现这种情况
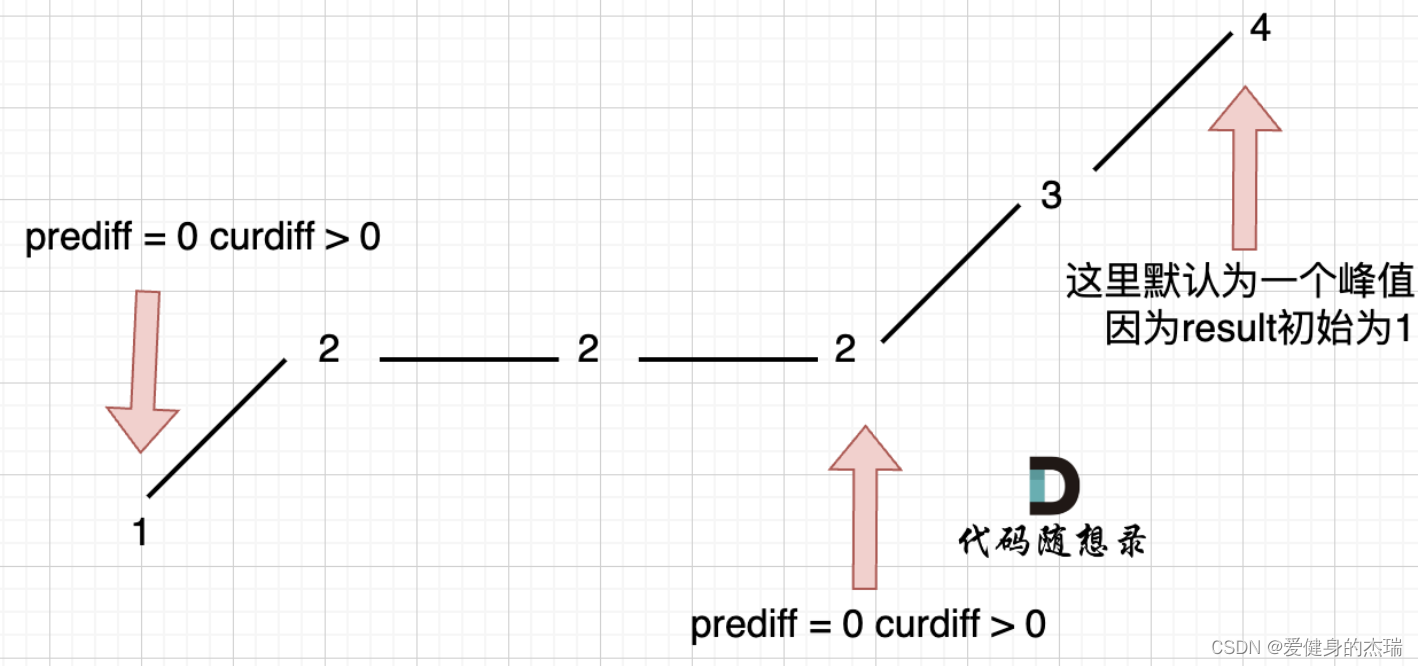
也就是当一开始我们把1算入答案后,pre_diff更新成2-1=1,这时候,按理来说除非再出现一个cur_diff的值小于0也就是折线图往下走的峰值,才能把2算入到答案中去,所以这意味着当我们更新完pre_diff之后,需要让他保持在1,而不是像上图这样在for循环的每一个循环中都让pre_diff = cur_diff,这样会出现错误,导致加入不该加的元素
Leetcode 53. 最大子数组和
讲解前:
这道题主要的思路是明白局部的最优解其实就是当前的子序列中能够得到的最大和是多少,如果我们遍历整个数组并且一个一个扩大我们的这个子序列,直到和数组一样大,我们就能找到所有的possible 子数组,同时我们又一直在计算子数组中最大的值是多少,这样就可以得到整体最优解了
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
res = float('-inf')
cur_sum = 0
for num in nums:
if cur_sum < 0:
cur_sum = num
else:
cur_sum = cur_sum + num
res = max(res, cur_sum)
return res然后呢做到这一点需要明白一个道理就是我们在遍历的时候,如果发现了当前的子数组和已经变成了负数,就是if statement 中的情况,那就要注意了,这意味着当遍历到下一个数字的时候,如果这个数字是负数,那只会让我们的连续和变得更小,如果这个数是正数,那么算上他还不如直接把他作为新的子数组的开始,还不用被拖累变小,所以无论正数还是负数,当我们目前的子数组连续和已经小于0了之后,就应该在下一个数字直接开启一个新的子数组,这就是局部的最优解,保证目前记录的子数组是包括当前数字的最大值
讲解后:
卡哥的讲解和我的一样,一样的思路