排序算法—快速排序

news2024/11/24 8:32:57

文章目录

  • 快速排序
    • 一、递归实现
    • 二、非递归实现
    • 总结

快速排序

以下均以排升序为最终目的。

一、递归实现

有一个排序能解决所有问题吗？没有！不过，快速排序这种排序适用于大多数情况。

我们前面讨论排序算法一般都是先讨论一趟的情况，对于快速排序，也是可以这么讨论的，特别的是，快速排序的每一趟的代码实现有三种不同的思路：挖坑法、左右指针法、前后指针法。

不管采用哪种思路，其目的都是：将某个选定的key值排到正确位置，然后使得key位置左边的所有值都小于key值，这个位置右边的所有值都大于key值，不过，key位置的左右并不是有序的。key值元素已经排好序了，不需要再参与后续的排序，因而将原序列分割成两个子区间（以排升序为例）。通常key选择序列中的最左边或最右边的元素。

在这里插入图片描述

挖坑法

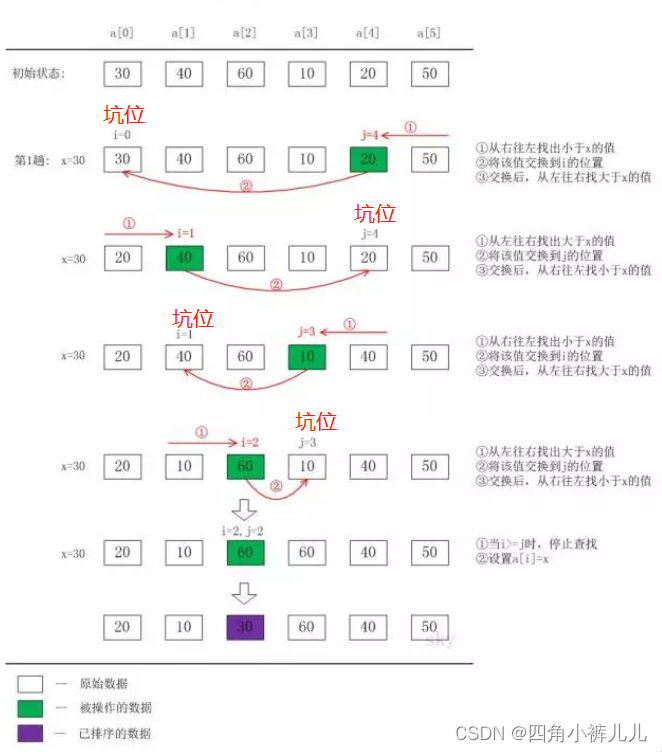
挖坑法选择一个值，放到变量key中，相当于备份了这个值，意味着这个值所在的位置可以被覆盖，称这样一个位置为 “坑”。假设key中存储的是序列最左边的元素，坑在左边，目的是实现升序排列。我们需要从最右边的元素开始遍历，寻找到比key值小的一个元素，用这个元素填坑，填坑后，填坑元素被备份，那么填坑元素的原位置成为新的坑。由于我们开始是从右开始遍历的，所以坑位更新后在右边，所以我们需要从左边开始遍历，寻找比key值大的元素，填坑，更新坑位，以此类推，当从左右遍历的指针相遇时，将它们指向的位置放上key值，此时一趟挖坑法结束。（推荐的思路）
在这里插入图片描述

左右指针法

左右指针法与挖坑法类似，选定一个key值，定义两个变量，起始指向序列最左边和最右边，两个指针开始向中间遍历，当左边的指针找到一个大于key的值，右边的指针找到一个小于key的值，则交换这两个位置的值，依次类推，最后将key值放到指定位置。（此方法不推荐，需要注意的细节太多了，很容易写错，掌握思路就好）

前后指针法

前后指针法较为抽象，选定最左边的元素为key，定义两个变量，假设cur、prev，prev初始指向key的的位置，cur初始指向key值后面一个元素，cur负责向右找比key小的值，如果找到了，prev++，然后交换prev和cur指向的两个位置的值，一直重复此过程，当cur要越界的时候停止，将prev指向的位置的值与key位置的值交换。(首推挖坑法，其次就是前后指针法）

以下是三种思路（每趟）的代码实现：

//挖坑法
int PartSort1(int* a, int left, int right)
{
    int begin = left;//从左遍历的下标
    int end = right;//从右遍历的下标
    int pivot = begin;//坑位下标
    int key = a[begin];//备份key值，初始坑位（这里选的是序列最左边元素）
    while (begin < end)
    {
        while (begin < end && a[end] >= key)
        {
            --end;
        }
        a[pivot] = a[end];
        pivot = end;
        while (begin < end && a[begin] <= key)//注意&&左边的语句，如果没有的话，可能会出现将一趟排序结果打乱的情况
        {
            ++begin;
        }
        a[pivot] = a[begin];
        pivot = begin;
    }
    a[pivot] = key;
    return pivot;
}



//左右指针法
int PartSort2(int* a, int left, int right)
{
    int begin = left;//左指针
    int end = right;//右指针
    int key = begin;
    while (begin < end)
    {
        while (begin < end && a[end] >= a[key])
        {
            --end;
        }
        while (begin < end && a[begin] <= a[key])
        {
            ++begin;
        }
        Swap(&a[begin], &a[end]);//交换函数
    }
    Swap(&a[begin], &a[key]);
    return begin;
}



//前后指针法
int PartSort3(int* a, int left, int right)
{
    int cur = left + 1;
    int prev = left;
    int key = left;
    while (cur <= right)
    {
        if (a[cur] < a[key] && ++prev != cur)
        {
            Swap(&a[prev], &a[cur]);
        }
        cur++;
    }
    Swap(&a[prev], &a[key]);
    return prev;
}

当结束一趟排好一个元素后，这个位置将序列分为了两个子区间，我们只要将这两个子区间排好序，那么就排序完毕。

对于每个子区间，采用相同的方式（挖坑法、前后指针法、左右指针法）排序，再将此子区间分割成两个新的子区间，基于这一特点，我们可以采用分治递归的方式解决。

以下每趟排序采用的是挖坑法。

void QuickSort(int* a, int left, int right)
{
    if (left >= right)
        return;
    int begin = left;
    int end = right;
    int key = a[begin];
    int pivot = begin;
    while (begin < end)
    {
        while (begin < end && a[end] >= key)
        {
            --end;
        }
        a[pivot] = a[end];
        pivot = end;
        while (begin < end && a[begin] <= key)
        {
            ++begin;
        }
        a[pivot] = a[begin];
        pivot = begin;
    }
    a[pivot] = key;
    QuickSort(a, left, pivot - 1);
    QuickSort(a, pivot + 1, right);
}

快速排序什么情况下最坏？时间复杂度是多少？

有序的情况下最差，这种情况下，每趟挖坑认为只能排好一个元素。

最坏的时间复杂度为O(N^2)

假如我们每次挖坑选择第一个元素为key，那么有序情况下，一趟挖坑分割的左子区间为空，所以只对右子区间执行挖坑法，每趟挖坑分割后的左子区间都是空，如果是排升序，那么从右找比key小的数要一直从右遍历到左边（因为原序列已经有序）。

针对这样的情况，采用三数取中
三数取中就是拿出序列中位置最左、最右和中间的三个元素，比较它们的大小，选出大小排序后为中间的元素。

这个元素将在后面被选定为key。

三数取中优化后的快速排序：

//三树取中
int GetmidIndex(int* a, int left, int right)
{
    int mid = (left + right) >> 1;
    if (a[left] > a[mid])
    {
        if (a[mid] > a[right])
        {
            return mid;
        }
        else if (a[left] > a[right])
        {
            return right;
        }
        else
            return left;
    }
    else//a[mid] > a[left]
    {
        if (a[mid] < a[right])
        {
            return mid;
        }
        else if (a[left] > a[right])
        {
            return left;
        }
        else
            return right;
    }
}
void QuickSort(int* a, int left, int right)
{
    if (left >= right)
    {
        return;
    }
    int index = GetmidIndex(a, left, right);/拿到中间大的元素的下标
    Swap(&a[left], &a[index]);//为了不影响后续最左边元素为key的逻辑，我们将三数取中得到的下标位置的值和序列最左边的值交换
    int begin = left;
    int end = right;
    int pivot = begin;
    int key = a[begin];
    while (begin < end)
    {
        while (begin < end && a[end] >= key)
        {
            --end;
        }
        a[pivot] = a[end];
        pivot = end;
        while (begin < end && a[begin] <= key)
        {
            ++begin;
        }
        a[pivot] = a[begin];
        pivot = begin;
    }
    a[pivot] = key;
    QuickSort(a, left, pivot - 1);
    QuickSort(a, pivot + 1, right);
}

我们还能继续优化吗？

对于数据总量庞大的情况，从头到尾递归快速排序，需要大量的递归调用，栈区空间占用较多。

不考虑其他情况，第一次挖坑为第一层；之后会出现两个子区间，这是第二层；接着4个子区间，第三层……我们发现越到后面，子区间越多，递归调用越多。

假如现在有100w（约等于2 ^ 20个数据，说明有20层，从后往前数2 ^ 19（50w）、2 ^ 18（25w）……我们发现大多数的函数调用都发生在后面的几层，而后面的几层处理的每个子区间的元素个数相对数据总量很少。

基于此，我们采用小区间优化消除后面几层的递归调用。

对小区间采用其他的排序方式，而不是继续递归调用，一般采用直接插入排序。

不过，小区间优化的效果并不明显，且要注意的是，到什么程度不递归，需要结合数据总量考虑，下面代码给的10。

三数取中、小区间优化后的快速排序：

int GetmidIndex(int* a, int left, int right)
{
    int mid = (left + right) >> 1;
    if (a[left] > a[mid])
    {
        if (a[mid] > a[right])
        {
            return mid;
        }
        else if (a[left] > a[right])
        {
            return right;
        }
        else
            return left;
    }
    else//a[mid] > a[left]
    {
        if (a[mid] < a[right])
        {
            return mid;
        }
        else if (a[left] > a[right])
        {
            return left;
        }
        else
            return right;
    }
}
void QuickSort(int* a, int left, int right)
{
    if (left >= right)
    {
        return;
    }
    int index = GetmidIndex(a, left, right);
    Swap(&a[left], &a[index]);
    int begin = left;
    int end = right;
    int pivot = begin;
    int key = a[begin];
    while (begin < end)
    {
        while (begin < end && a[end] >= key)
        {
            --end;
        }
        a[pivot] = a[end];
        pivot = end;
        while (begin < end && a[begin] <= key)
        {
            ++begin;
        }
        a[pivot] = a[begin];
        pivot = begin;
    }
    a[pivot] = key;
    
    if (pivot - 1 - left < 10)//判断区间是否为小区间
    {
        InsertSort(a + left, pivot - 1 - left + 1);//插入排序
    }
    else
        QuickSort(a, left, pivot - 1);//递归
    if (right - pivot - 1 < 10)
    {
        InsertSort(a + pivot + 1, right - pivot - 1 + 1);
    }
    else
        QuickSort(a, pivot + 1, right);
}

二、非递归实现

递归的缺陷： 栈帧深度太深，栈空间不够用，可能会溢出

递归改非递归：

  • 直接改循环
  • 借助数据结构栈模拟递归过程

非递归实现快速排序需要用到栈。

想清楚，递归建立栈帧，栈帧存储局部变量，我们函数调用时存储的是区间，也就是 left 和 right，我们考虑用栈来模拟递归，存储left和right的值。

思路

每次将区间的左右下标入栈，每趟排序从栈顶拿取，这一过程要考虑栈的先入后出属性。

由于C语言限制，其库函数没有现成的栈，我们需要独立去实现一个栈。

独立实现的栈：

//Stack.h
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

typedef int STDataType;
typedef struct StackNode
{
    STDataType* a;
    int top;
    int capacity;
}ST;

void StackInit(ST* ps);
void StackPush(ST* ps, STDataType x);
void StackPop(ST* ps);
void StackDestory(ST* ps);
STDataType StackTop(ST* ps);
bool StackEmpty(ST* ps);
int StackSize(ST* ps);

//Stack.c
#include "Stack.h"

void StackInit(ST* ps)
{
    assert(ps);
    STDataType* tmp = (STDataType*)malloc(sizeof(STDataType) * 4);
    if(NULL == tmp)
    {
        printf("malloc fail\n");
        exit(-1);
    }
    else
    {
        ps->a tmp;
        ps->capacity = 4;
        ps->top = 0;
    }
}


void StackPush(ST* ps, STDataType x)
{
    assert(ps);
    if(ps->capacity == ps->top)
    {
        STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * ps->capacity * 2);
        if(NULL == tmp)
        {
            printf("realloc fail\n");
            exit(-1);
        }
        else
        {
            ps->a = tmp;
            ps->capacity *= 2;
            ps->a[ps->top] = x;
            ps->top++;
        }
    }
}


void StackPop(ST* ps)
{
    assert(ps);
    assert(ps->top > 0);
    ps->top--;
}


void StackDestory(ST* ps)
{
    assert(ps);
    free(ps->a);
    ps->a = NULL;
    ps->top = ps->capacity = 0;
}


STDataType StackTop(ST* ps)
{
    assert(ps);
    assert(ps->top > 0);
    return ps->a[ps->top-1];
}


bool StackEmpty(ST* ps)
{
    assert(ps);
    return ps->top == 0;
}


int StackSize(ST* ps)
{
    assert(ps);
    return ps->top;
}

基于上面栈的实现，我们实现一下非递归快速排序。

void QuickSortNonr(int* a, int len)
{
    ST st;
    StackInit(&st);
    StackPush(&st, len - 1);//第一趟排序区间入栈
    StackPush(&st, 0);
    while (!StackEmpty(&st))//栈为空则排序证明所有子区间排序完毕
    {
        int left = StackTop(&st);
        StackPop(&st);
        int right = StackTop(&st);
        StackPop(&st);
        
        int index = GetmidIndex(a, left, right);
        Swap(&a[left], &a[index]);
        
        int end = right;
        int begin = left;
        int pivot = begin;
        int key = a[begin];
        
        while (begin < end)
        {
            while (begin < end && a[end] >= key)
            {
                --end;
            }
            a[pivot] = a[end];
            pivot = end;
            while (begin < end && a[begin] <= key)
            {
                ++begin;
            }
            a[pivot] = a[begin];
            pivot = begin;
        }
        a[pivot] = key;
        
        if (right > pivot + 1)//子区间不存在或只有一个元素不入栈
        {
            StackPush(&st, right);
            StackPush(&st, pivot + 1);
        }
        
        if (left < pivot - 1)
        {
            StackPush(&st, pivot - 1);
            StackPush(&st, left);
        }
    }
    StackDestory(&st);
}

总结

1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序。

2. 时间复杂度：O(N*logN)
最坏情况下：O(N^2)
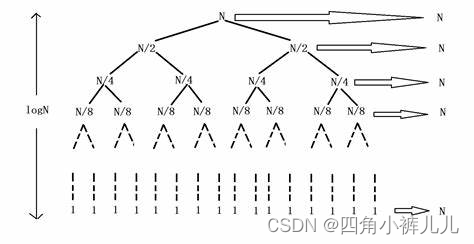
在这里插入图片描述

3. 空间复杂度：O(logN)

4. 稳定性：不稳定

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1580913.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

传输层 --- TCP (上篇)

传输层 --- TCP (上篇)

目录 1. TCP 1.1. TCP协议段格式 1.2. TCP的两个问题 1.3. 如何理解可靠性 1.4. 理解确认应答机制 2. TCP 报头中字段的分析 2.1. 序号和确认序号 2.1.1. 序号和确认序号的初步认识 2.1.2. 如何正确理解序号和确认序号 2.2. TCP是如何做到全双工的 2.3. 16位窗口大小…
阅读更多...
TypeScript系列之-理解TypeScript类型系统画图讲解

TypeScript系列之-理解TypeScript类型系统画图讲解

TypeScript的输入输出 如果我们把 Typescript 编译器看成一个黑盒的话。其输入则是使用 TypeScript 语法书写的文本或者文本集合。 输出是编译之后的 JS 文件 和 .d.ts 的声明文件 其中 JS 是将来需要运行的文件(里面是没有ts语法&#xff0c;有一个类型擦除的操作)&#xff0…
阅读更多...
Shopee虾皮100%有效提高广告效果的案例分享

Shopee虾皮100%有效提高广告效果的案例分享

Shopee 店铺运营中存在三种广告类型&#xff0c;分别是:关键词广告、关联广告和店铺广告。其中使用最为普遍&#xff0c;主控权最为直接的就是关键词广告&#xff0c;TA的适用范围最广&#xff0c;起效最快&#xff0c;并且可根据自身运营的能力去调控投入产出比&#xff0c;深…
阅读更多...
【Python】基础（专版提升1）

【Python】基础（专版提升1）

Python基础 1. 导学1.1 学习理念1.1.1 弱语法&#xff0c;重本质1.1.2 是技术&#xff0c;更艺术 1.2 学习方法1.2.1 当天知识必须理解 2. Python 简介2.1 计算机基础结构2.1.1 硬件2.1.2 软件 2.2 基础知识2.2.1 Python介绍2.2.1.1定义2.2.1.2优势2.2.1.3从业岗位 2.2.2 Pytho…
阅读更多...
数学基础：常见函数图像

数学基础：常见函数图像

来自&#xff1a; https://www.desmos.com/calculator/l3u8133jwj?langzh-CN 推荐: https://www.shuxuele.com/index.html 一、三角函数 1.1 正弦 sin(x) 1.2 余弦 cos(x) 1.3 正切 tan(x) 1.4 余切 cot(x) 1.5 正弦余弦综合 1.6 正切余切综合 二、指数对数
阅读更多...
[C语言]——柔性数组

[C语言]——柔性数组

目录 一.柔性数组的特点 二.柔性数组的使用 三.柔性数组的优势 C99中&#xff0c;结构体中的最后⼀个元素允许是未知大小的数组&#xff0c;这就叫做『柔性数组』成员。 typedef struct st_type //typedef可以不写 { int i;int a[0];//柔性数组成员 }type_a; 有些编译器会…
阅读更多...
14：00面试，15：00才出来，直接给我问麻了。。

14：00面试，15：00才出来，直接给我问麻了。。

从小厂出来&#xff0c;没想到在另一家公司又寄了。 到这家公司开始上班&#xff0c;加班是每天必不可少的&#xff0c;看在钱给的比较多的份上&#xff0c;就不太计较了。没想到3月一纸通知&#xff0c;所有人不准加班&#xff0c;加班费不仅没有了&#xff0c;薪资还要降40%…
阅读更多...
基础语法复习

基础语法复习

常用的定义&#xff1a; 读取数据加速&#xff1a; input sys.stdin.readline 设置递归深度&#xff1a; sys.setrecursionlimit(100000) 记忆化搜索&#xff1a; from functools import lru_cache lru_cache(maxsizeNone) 计数器&#xff1a; Counter 类是一个非常有…
阅读更多...
Spring Cloud微服务入门（五）

Spring Cloud微服务入门（五）

Sentinel的安装与使用 安装部署Sentinel 下载Sentinel&#xff1a; https://github.com/alibaba/Sentinel/releases Sentinel控制台 https://localhost:8080 用户和密码为sentinel 使用Sentinel 加依赖&#xff1a; 写配置&#xff1a; 输入&#xff1a; java -Dserver.po…
阅读更多...
【React】React hooks 清除定时器并验证效果

【React】React hooks 清除定时器并验证效果

React hooks 清除定时器并验证效果 目录结构如下useTime hookClock.tsx使用useTime hookApp.tsx显示Clock组件显示时间&#xff08;开启定时器&#xff09;隐藏时间&#xff08;清除定时器&#xff09; 总结参考 目录结构如下 useTime hook // src/hooks/common.ts import { u…
阅读更多...
lora微调过程

lora微调过程

import os import pickle from transformers import AutoModelForCausalLM from peft import get_peft_config, get_peft_model, get_peft_model_state_dict, LoraConfig, TaskTypedevice "cuda:0"#1.创建lora微调基本的配置 peft_config LoraConfig(task_typeTask…
阅读更多...
CAN和LIN的DB9接口定义

CAN和LIN的DB9接口定义

文章目录 前言一、DB9实物及引脚二、LIN DB9三、CAN DB9总结前言 在日常汽车总线测试中，最主要的通信网络就是CAN网络，小伙伴们在测试时，经常会遇到使用DB9插头来测试、录取CAN总线报文，但是DB9插头内有9个插针，哪2个才是CAN-H和CAN-L呢？ 一、DB9实物及引脚 DB9 接口是…
阅读更多...
杨辉三角形（蓝桥杯，acwing）

杨辉三角形（蓝桥杯，acwing）

题目描述&#xff1a; 下面的图形是著名的杨辉三角形&#xff1a; 如果我们按从上到下、从左到右的顺序把所有数排成一列&#xff0c;可以得到如下数列&#xff1a; 1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ... 给定一个正整数 N&#xff0c;请你输出数列中第一次出现…
阅读更多...
实验：基于Red Hat Enterprise Linux系统建立逻辑卷并进行划分

实验：基于Red Hat Enterprise Linux系统建立逻辑卷并进行划分

目录 一. 实验目的 二. 实验内容 三. 实验设计描述及实验结果 1. 为虚拟机添加三块大小为5GB的磁盘nvme0n2 nvme0n3 nvme0n4 2. 将三块硬盘转换为物理卷&#xff0c;并将nvme0n2 nvme0n3两pv建立成名为"自己名字_vg“的卷组&#xff0c;并将nvme0n4扩展进该卷组。 LVM管…
阅读更多...
os.listdir()bug总结

os.listdir()bug总结

今天测试出一个神奇的bug&#xff0c;算是教训吧&#xff0c;找了两天不知道问题在哪&#xff0c;最后才发现问题出现在这 原始文件夹显示 os.listdir()结果乱序 import os base_path "./file/"files os.listdir(base_path)print(files)问题原因 解决办法(排序) …
阅读更多...
【论文解读】大模型事实性调查（上）

【论文解读】大模型事实性调查（上）

一、简要介绍 本调查探讨了大型语言模型&#xff08;llm&#xff09;中的事实性的关键问题。随着llm在不同领域的应用&#xff0c;其输出的可靠性和准确性变得至关重要。论文将“事实性问题”定义为llm产生与既定事实不一致的内容的概率。论文首先深入研究了这些不准确性的含义…
阅读更多...
IO-DAY8

IO-DAY8

使用消息队列去实现2个终端之间的互相聊天 要求:千万不要做出来2个终端之间的消息发送是读一写的&#xff0c;一定要能够做到&#xff0c;一个终端发送n条消息&#xff0c;另一个终端一条消息都不回复 A终端&#xff1a; #include<myhead.h> typedef struct msgbuf {lon…
阅读更多...
B02、执行引擎-5

B02、执行引擎-5

1、前言 1.1、什么是机器码 各种用二进制编码方式表示的指令&#xff0c;叫做机器指令码。开始&#xff0c;人们就用它采编写程序&#xff0c;这就是机器语言。机器语言虽然能够被计算机理解和接受&#xff0c;但和人们的语言差别太大&#xff0c;不易被人们理解和记忆&#x…
阅读更多...
基于SSM框架实现的在线心理评测与咨询系统(技术栈 spring+springmvc+mybatis+jsp+jquery+css)

基于SSM框架实现的在线心理评测与咨询系统(技术栈 spring+springmvc+mybatis+jsp+jquery+css)

一、项目简介 本项目是一套基于SSM框架实现的在线心理评测与咨询系统&#xff0c;主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的Java学习者。 包含&#xff1a;项目源码、数据库脚本等&#xff0c;该项目附带全部源码可作为毕设使用。 项目都经过严格调试&am…
阅读更多...
小白学Java成长日记特别篇

小白学Java成长日记特别篇

晚上好&#xff0c;各位小伙伴。今天给大家带来的是Java的输出补充篇&#xff0c;前两篇说了输出和输入的大概&#xff0c;但我没有详细讲它俩&#xff0c;因此这篇文章来详细的聊一聊它俩。那么废话不多说&#xff0c;我们赶紧进入正题。 首先讲一讲这个Java的输出吧。 输出格…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023