题目描述:
下面的图形是著名的杨辉三角形:
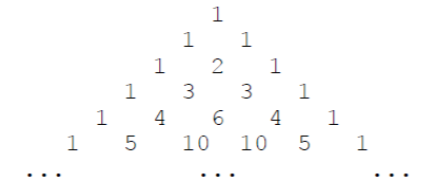
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列:
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...
给定一个正整数 N,请你输出数列中第一次出现 N 是在第几个数?
输入格式:
输入一个整数 N。
输出格式:
输出一个整数代表答案。
数据范围:
对于 20% 的评测用例,1≤N≤10;
对于所有评测用例,1≤N≤1e9。
输入样例:
6
输出样例:
13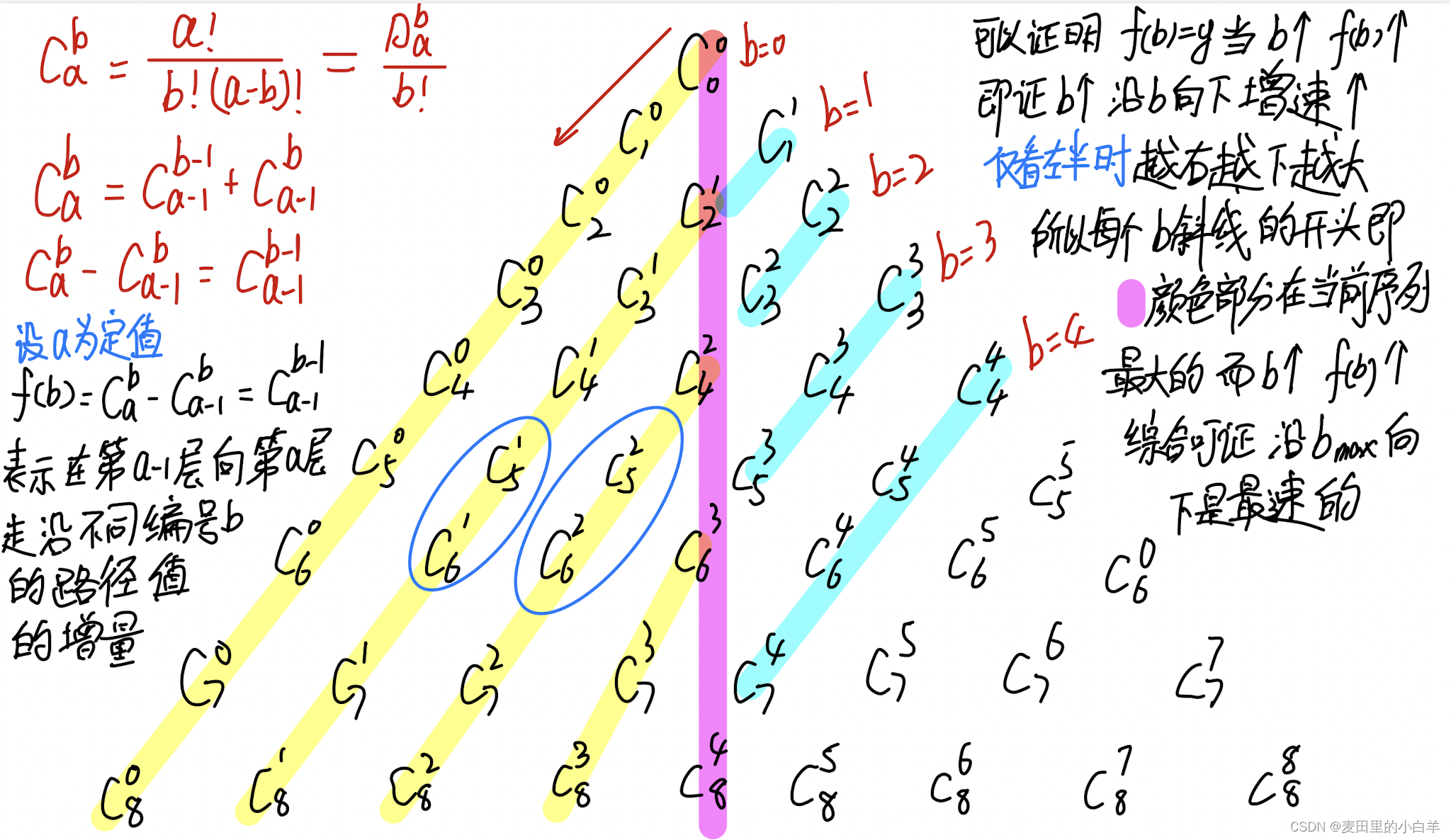
这个图是来自acwing的东风祝酒的图片
分析步骤:
第一:理清思路:
-
众所周知,杨辉三角中华瑰宝,他这个三角型是对称的,如果我们要求出哪个点是第一次出现的,那么一定是在这个三角形的左边!我们可以把右半部分删掉,完全不用考虑。这是本题目第一个特点。
-
现在我们再斜着看一看,把斜着的看做一个序列。第一行数坐标就是(0,0),第二行从左到右就是(1,0),(1,1).....以此类推。我们再看到中间紫色的这一列数值永远就是C2k^k并且永远是这个数最大,我们就可以从这个数开始找起。而且题目中说到了N最大就是1e9,那么C34^17>1e9 ; C32^16<1e9。所以我只需要找前面16个斜行就行了。这是本题的第二个特点。
-
我们现在想想,如果一个一个去找的话速度太慢了。因为序列的单调的这一眼就能看出来,而且我们需要找一个特定的,在这个值的左边就会太小了,在这个值的右边就会太大了,就可以将其分为两个部分。这就符合了我们二分的特点,因此我们直接从中间对称轴倒序二分找起即可!这就是本题的第三个特点。
-
大家一定要好好看看这图,仔细去理解!!
第二:书写主函数,构建整体框架:
-
因为我们分析过了我们只需要枚举前16行就可以了,那么我们倒序枚举,检查一下这一行是不是我们想要的,是的话就代表找到了,就break退出。
int main()
{
cin >> n;
for (int k = 16; ; k -- )
if (check(k))
break;
return 0;
}第三:书写check函数:
-
现在我们就入了其中的一个序列进行检查,运用二分的方法去查找。
-
首先我们要确定二分的左节点和右节点,所以我们定义LL l = k * 2, r = n;为什么这么定义呢?因为:在一个序列之中我们最小的值是上图中紫色的那一些数,这些数的特点是C2k^k,所以定义他们为最小的左边界节点,那么右边界节点就应该是最大的那个数字了,但是我们的杨辉三角是无穷的所以我们应该只需要找到题目给出的那个数字就可以了,那么这个数一定会在Cn^1的这个地方出现,因为这个值就是N。所以我们把右边界定义为n。
-
如果l比r都要大就直接返回false不可能在这一行。因为这个数一定比这一序列的第一个数要小,就代表答案的位置在更靠前的序列之中。
-
进入while循环,计算我们的mid值计算我们的Cmid^k让这个数和n比较大小。如果这个数比n要大或等于的话就代表答案有可能在mid左边也就是更小的那一边,所以我们把r赋值给mid。反之答案比n更小的话,那么答案一定在mid的右边也就是更大的一边,就让mid+1赋值给l。
-
经过了一轮的while循环判断之后,再去计算一下Cr^k看看和答案是否一致,如果不一致就是错
-
最终输出位置即可。
bool check(int k)
{
LL l = k * 2, r = n;
if (l > r) return false;
while (l < r)
{
LL mid = l + r >> 1;
if (C(mid, k) >= n) r = mid;
else l = mid + 1;
}
if (C(r, k) != n) return false;
cout << r * (r + 1) / 2 + k + 1 << endl;
return true;
}第四:书写计算组合数的函数:
-
我们计算组合数直接暴力做就可以,利用双指针一起去求解。
LL C(int a, int b)
{
LL res = 1;
for (int i = a, j = 1; j <= b; i --, j ++ )
{
res = res * i / j;
if (res > n) return res;
}
return res;
}代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
int n;
LL C(int a, int b)
{
LL res = 1;
for (int i = a, j = 1; j <= b; i --, j ++ )
{
res = res * i / j;
if (res > n) return res;
}
return res;
}
bool check(int k)
{
LL l = k * 2, r = n;
if (l > r) return false;
while (l < r)
{
LL mid = l + r >> 1;
if (C(mid, k) >= n) r = mid;
else l = mid + 1;
}
if (C(r, k) != n) return false;
cout << r * (r + 1) / 2 + k + 1 << endl;
return true;
}
int main()
{
cin >> n;
for (int k = 16; ; k -- )
if (check(k))
break;
return 0;
}