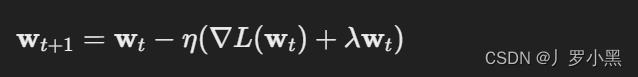机器学习模型——GBDT和Xgboost

GBDT基本概念：

GBDT（Gradient Boosting Decision Tree，简称GBDT）梯度提升决策树，是Gradient Boost 框架下使用较多的一种模型，且在GBDT中，其基学习器是分类回归树也就是CART，且使用的是CART树中的回归树。

GBDT这个算法还有一些其他的名字, MART（Multiple Additive Regression Tree)，GBRT（Gradient Boost Regression Tree)，Tree Net，Treelink等。

GBDT算法原理以及实例理解（含Python代码简单实现版）-CSDN博客

GBDT算法原理以及实例理解_gbdt算法实例 csdn-CSDN博客

https://blog.csdn.net/lgh1700/article/details/100093316 回归问题

https://blog.csdn.net/RuDing/article/details/78332192 参数

https://www.cnblogs.com/always-fight/p/9400346.html 平方损失计算

决策树：

决策树分为两大类：回归树和分类树。前者用于预测实数值，如明天的温度、用户的年龄、网页的相关程度；后者用于分类标签值，如晴天/阴天/雾/雨、用户性别、网页是否是垃圾页面。这里要强调的是，前者的结果加减是有意义的，如10岁+5岁-3岁=12岁，后者则无意义，如男+男+女=到底是男是女？

GBDT的核心在于累加所有树的结果作为最终结果，就像前面对年龄的累加（-3是加负3），而分类树的结果显然是没办法累加的，所以GBDT中的树都是回归树，不是分类树，这点对理解GBDT相当重要（尽管GBDT调整后也可用于分类但不代表GBDT的树是分类树）。GBDT很适用二分类

GBDT算法原理：

GBDT也是继承了Boosing的思想，利用加法模型与前向分布算法实现学习的优化过程。每个基学习器在上一轮学习器的基础上进行训练。对弱学习器（弱分类器）的要求一般足够简单，并且是低方差和高偏差的（欠拟合）。因为训练的过程就是通过降低偏差不断提高最终学习器的精度。

加法模型：本质就是我们要得到的最终预测结果是由前面M个弱学习器拟合的结果相加得到。如果我们用 T(x；θ_m)表示第m棵决策树；θ_m表示决策树的参数；M为树的个数。强分类器f_M(x)可以由多个弱分类器T(x;θ_m)线性相加而成。则加法模型可表述为：

前项分步算法：第m步的模型可以写成：

可以理解为当前树模型等于前一棵树的模型加上刚生成树的模型（递归）

GBDT的核心：

GBDT的核心就在于，每一棵树学习的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。

比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁。如果我们的迭代轮数还没有完，可以继续迭代下面每一轮迭代，拟合的岁数误差都会减小。

GBDT的目标函数：

模型一共训练M轮，每轮产生一个弱学习器T（x;θ_m)。弱学习器的目标函数可以表示为：

F_m−1(x_i)为当前的模型，GBDT通过经验风险极小化来确定下一个弱学习器的参数。具体使用到的损失函数的选择也就是这里的L（)，主要有平方损失函数，0-1损失函数，对数损失函数等等。如果我们选择平方损失函数，那么这个差值其实就是我们平常所说的残差。目标：第一个是希望我们的损失函数能够不断减小；第二个是希望我们的损失函数能够尽可能快地减小。

https://blog.csdn.net/qq_35269774/article/details/88593661 回归树

目标函数的优化：

让损失函数沿着负梯度方向的下降，是GBDT的GB另外一个核心。利用损失函数的负梯度在当前模型的值，作为回归提升树算法中的残差的近似值去拟合一个回归树。GBDT每轮迭代的时候，都去拟合损失函数在当前模型下的负梯度。

这样每轮训练的时候都能够让损失函数尽可能快的减小，尽快地收敛达到局部最优或者全局最优。

GBDT代码实现：

from sklearn.datasets import load_iris
iris = load_iris()

from sklearn.ensemble import GradientBoostingClassifier,GradientBoostingRegressor
# 既可以做分类，也可以做回归
GBDT = GradientBoostingClassifier()

X = iris['data']
y = iris['target']

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)

GBDT.fit(X_train,y_train)

print(GBDT.score(X_test,y_test))

0.9555555555555556

准确率还是很高的

由于GBDT不经常用于回归，因此我就不演示了

Xgboost基本概念：

XGBoost本质上还是GBDT，但是把速度和效率做到了极致；

不同于传统的GBDT方式，只利用了一阶的导数信息，XGBoost对损失函数做了二阶的求导（泰勒展开），并在目标函数之外加入了正则项整体求最优解，用以权衡目标函数的下降和模型的复杂程度，避免过拟合。

https://www.jianshu.com/p/ac1c12f3fba1 详解

https://www.cnblogs.com/mantch/p/11164221.html

XGboost的目标函数：

XGBoost继承了GBDT，模型也是CART, 但不仅限于回归树。因此还是沿用了加法模型，但是在目标函数上有所区别。

目标函数：XGboost的目标函数包含了两个部分，第一部分还是损失函数，第二部分就是正则项。而且这里的正则化项是由K颗树的正则化项相加而来。

正则项的作用主要是为了防止过拟合，提高准确率。

XGboost的损失函数：

XGboost在损失函数项采用的是二阶求导，损失函数也就可以表示为如下：

其中g_i和ℎ_i分别是泰勒展开的一次式和二次式的系数。而且g_i和ℎ_i是不依赖于损失函数的形式的，只要这个损失函数满足二次可微即可。也就是说，XGboost是可以支持自定义损失函数的。

在迭代更新的过程中g_i和ℎ_i 是可以并行计算的，因此，XGboost可以在提高准确率的同时还可以提高运算速度。

XGboost的正则化项：

XGboost的应用：

近年来，在电子商务网站进行在线购物逐渐成为人们新的购物习惯。在线购物过程中，人们在最终决定购买某种商品前，通常会在电子商务平台留下大量的信息，这些信息通常反映了用户购物的行为模式。通过数据挖掘方法来分析用户的行为模式数据，有利于更好地了解用户的购物习惯和倾向性，从而为预测用户的购买行为提供可能。

将XGBoost引入到电子商务的商品推荐算法中，挖掘用户在电子商务平台的行为数据信息，建立分类预测模型，从而个性化地向用户推荐商品。结果表明，与传统机器学习算法相比，XGBoost具有速度快、准确度高等优势。

XGboost和GBDT的不同：

传统GBDT以CART作为基分类器，XGboost还支持线性分类器，这个时候XGboost相当于带L1和L2正则化项的逻辑回归（分类问题）或者线性回归（回归问题）。

传统GBDT在优化时只用到一阶导数信息，XGboost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。

XGboost在代价函数里加入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。正则项降低了模型的复杂度，使学习出来的模型更加简单，防止过拟合，这也是XGboost优于传统GBDT的一个特性。

Shrinkage（缩减），相当于学习速率（XGboost中的eta）。XGboost在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间。实际应用中，一般把eta设置得小一点，然后迭代次数设置得大一点。

列抽样（column subsampling)。XGboost借鉴了随机森林的做法，支持列抽样，不仅能降低过拟合，还能减少计算，这也是XGboost异于传统GBDT的一个特性。

XGboost代码实现：

from sklearn.datasets import load_iris
iris = load_iris()

from xgboost.sklearn import XGBClassifier
xgb = XGBClassifier()

X = iris['data']
y = iris['target']

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)

xgb.fit(X_train,y_train)

print(xgb.score(X_test,y_test))

0.9333333333333333