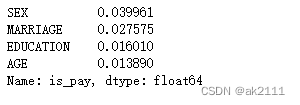
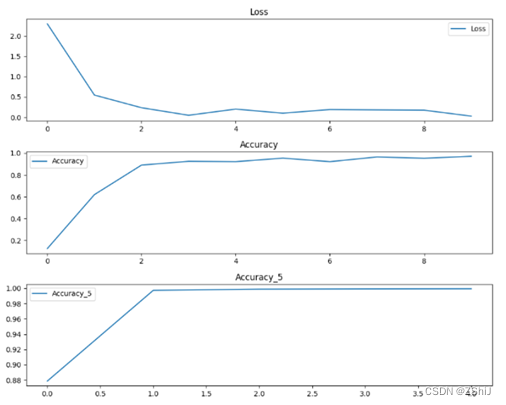
题目：一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。现求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

题目分析：

• 当 n 等于 1 时，青蛙只能跳一级台阶到达，因此只有一种跳法，直接返回 1。
• 当 n 等于 2 时，青蛙可以选择跳一级或跳两级来到达，因此有两种跳法，直接返回 2。
• 对于 n 大于 2 的情况，青蛙可以跳一级到第 n-1 级台阶，或者青蛙可以跳两级到第 n-2 级台阶，此时跳1级的跳法剩下1级台阶，跳2级的跳法剩下2级台阶，对于剩下1级台阶时，正好符合n == 1的情况，当剩下2级台阶时，正好符合n == 2的情况。
• 因此，n > 2时，就是分别计算n-1与n-2的可能次数，相对应的就是跳1级台阶的跳法与跳2级台阶的跳法。为什么要进行n-1与n-2呢？因为跳1级台阶跳到n-1时，只剩1级台阶，程序就会走n == 1的情况，跳2级台阶跳到n-2时，只剩2级台阶，程序就会走n == 2的情况。
• 最后将两种情况相加。
• 看看代码吧：

//青蛙跳台阶问题
//类似于斐波那契数
int frogJump(int n)
{
	//当台阶数为1时，只有1种跳法
	if (1 == n)
		return 1;
	//当台阶数为2时，只有2种跳法
	if (2 == n)
		return 2;
	//forgJump(n - 1)的作用为所有跳1层台阶的可能次数
	//forgJump(n - 2)的作用为所有跳2层台阶的可能次数
	//最后相加 == 总可能次数
	//n-1与n-2的意思为，从n直到剩下1层台阶，从n直到剩下2层台阶，然后就会进入n==1或n==2
	//进行返回
	return frogJump(n - 1) + frogJump(n - 2);
}
int main()
{
	int n = 0; //台阶数
	scanf("%d", &n);
	int count = frogJump(n);
	printf("跳法:%d\n", count);
	return 0;
}

如果您还理解不了，来看看代码图解吧：

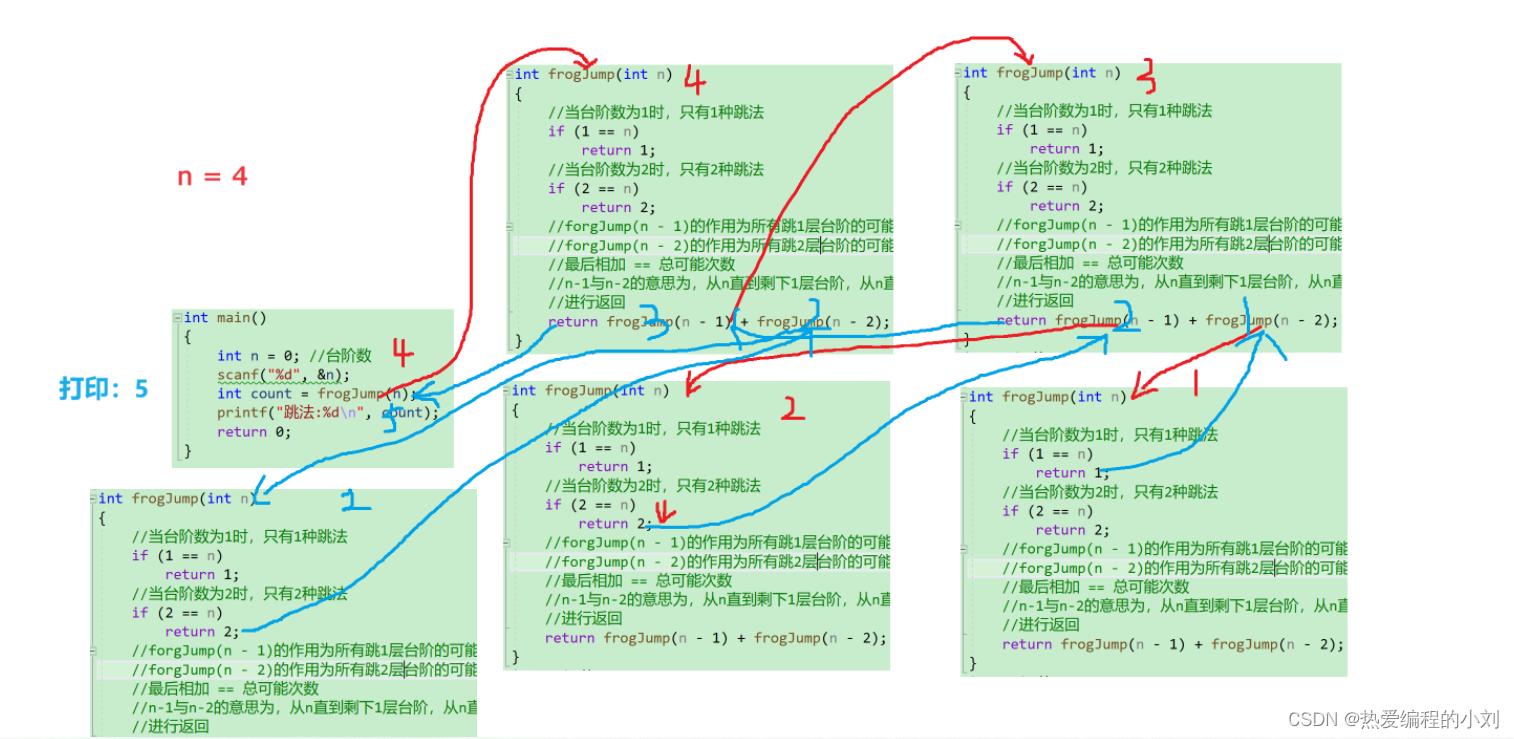
这种递归方法虽然直观易懂，但是对于较大的n值，会导致大量的重复计算，效率较低。在实际应用中，我们通常会使用动态规划方法来避免这种重复计算，提高算法的效率。

---