代码随想录算法训练营第8天 344.反转字符串、541. 反转字符串II、剑指Offer58-II.左旋转字符串
反转字符串
力扣题目链接(opens new window)
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
对于字符串,我们定义两个指针(也可以说是索引下标),一个从字符串前面,一个从字符串后面,两个指针同时向中间移动,并交换元素。
以字符串hello为例,过程如下:

swap可以有两种实现。
一种就是常见的交换数值:
int tmp = s[i];
s[i] = s[j];
s[j] = tmp;
一种就是通过位运算:
s[i] ^= s[j];
s[j] ^= s[i];
s[i] ^= s[j];
/**
* @description: 反转字符串
* @author: 刘宇浩
* @date: 2023/1/10 1:02
*/
public class ReverseString {
public void reverseString(char[] s) {
int left = 0;
int right = s.length - 1;
char temp = ' ';
while (left < right) {
temp = s[left];
s[left] = s[right];
s[right] = temp;
left++;
right--;
}
}
}
反转字符串II
力扣题目链接(opens new window)
给定一个字符串 s 和一个整数 k,从字符串开头算起, 每计数至 2k 个字符,就反转这 2k 个字符中的前 k 个字符。
如果剩余字符少于 k 个,则将剩余字符全部反转。
如果剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样。
其实在遍历字符串的过程中,只要让 i += (2 * k),i 每次移动 2 * k 就可以了,然后判断是否需要有反转的区间。
因为要找的也就是每2 * k 区间的起点,这样写,程序会高效很多。
/**
* @description: 反转字符串 II
* @author: 刘宇浩
* @date: 2023/1/10 1:05
*/
public class ReverseStr {
public String reverseStr(String s, int k) {
char[] ch = s.toCharArray();
for (int i = 0; i < ch.length; i += 2 * k) {
int start = i;
// 判断尾数够不够k个来取决end指针的位置
int end = Math.min(ch.length - 1, start + k - 1);
while (start < end) {
char temp = ch[start];
ch[start] = ch[end];
ch[end] = temp;
start++;
end--;
}
}
return new String(ch);
}
}
左旋转字符串
力扣题目链接(opens new window)
字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如,输入字符串"abcdefg"和数字2,该函数将返回左旋转两位得到的结果"cdefgab"。
这道题目也非常类似,依然可以通过局部反转+整体反转 达到左旋转的目的。
具体步骤为:
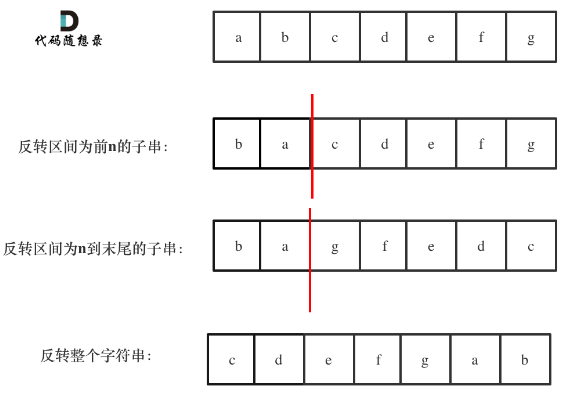
- 反转区间为前n的子串
- 反转区间为n到末尾的子串
- 反转整个字符串
最后就可以达到左旋n的目的,而不用定义新的字符串,完全在本串上操作。
例如 :示例1中 输入:字符串abcdefg,n=2
如图:
/**
* @description: 左旋转字符串
* @author: 刘宇浩
* @date: 2023/1/10 14:07
*/
public class ReverseLeftWords {
public String reverseLeftWords(String s, int n) {
int len = s.length();
StringBuilder str = new StringBuilder(s);
reverse(str,0,n-1);
reverse(str,n,len-1);
return str.reverse().toString();
}
public void reverse(StringBuilder sb, int start, int end) {
while (start < end) {
char temp = sb.charAt(start);
sb.setCharAt(start, sb.charAt(end));
sb.setCharAt(end, temp);
start++;
end--;
}
}
}