几道基础的二叉树、树的题
- LeetCode144.二叉树的前序遍历
- 思路及实现
- 方法一:递归
- 方法二:迭代
- LeetCode145.二叉树的后序遍历
- 思路及实现
- 方法一:递归
- 方法二:迭代
- LeetCode94.二叉树的中序遍历
- 思路及实现
- 方法一:递归
- 方法二:迭代
- LeetCode559. N 叉树的最大深度
- 题目描述
- 思路及实现
- 方法一:DFS
- 方法二:BFS
- LeetCode589. N 叉树的前序遍历
- 思路及实现
- 方法一:递归
- 方法二:迭代
- LeetCode590. N 叉树的后序遍历
- 思路及实现
- 方法一:递归
- 方法二:迭代
递归方法很简单,要学学迭代方法呃
LeetCode144.二叉树的前序遍历
题源 👉 144. 二叉树的前序遍历 - 力扣(LeetCode)
思路及实现
方法一:递归
class Solution {
List<Integer> ans = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
dfs(root);
return ans;
}
public void dfs(TreeNode root){
if(root == null) return;
ans.add(root.val);
dfs(root.left);
dfs(root.right);
}
}
方法二:迭代
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> ans = new ArrayList<>();
if(root == null) return ans;
Deque<TreeNode> d = new ArrayDeque<>();
d.addLast(root);
while(!d.isEmpty()){
TreeNode node = d.pollLast();
ans.add(node.val);
if(node.right != null) d.addLast(node.right);
if(node.left != null) d.addLast(node.left);
}
return ans;
}
}
LeetCode145.二叉树的后序遍历
题源 👉 144. 二叉树的前序遍历 - 力扣(LeetCode)
思路及实现
方法一:递归
class Solution {
List<Integer> ans = new ArrayList<>();
public List<Integer> postorderTraversal(TreeNode root) {
dfs(root);
return ans;
}
public void dfs(TreeNode node){
if(node == null) return;
dfs(node.left);
dfs(node.right);
ans.add(node.val);
}
}
方法二:迭代
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> ans = new ArrayList<>();
if(root == null) return ans;
Deque<TreeNode> d = new ArrayDeque<>();
d.addLast(root);
while(!d.isEmpty()){
TreeNode node = d.pollLast();
ans.add(node.val); // 按中右左输入list,最后再将list翻转,实现后序遍历
if(node.left != null) d.addLast(node.left);
if(node.right != null) d.addLast(node.right);
}
Collections.reverse(ans); // list翻转
return ans;
}
}
LeetCode94.二叉树的中序遍历
题源 👉 144. 二叉树的前序遍历 - 力扣(LeetCode)
思路及实现
方法一:递归
class Solution {
List<Integer> ans = new ArrayList<>();
public List<Integer> inorderTraversal(TreeNode root) {
dfs(root);
return ans;
}
public void dfs(TreeNode root){
if(root == null) return;
dfs(root.left);
ans.add(root.val);
dfs(root.right);
}
}
方法二:迭代
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> ans = new ArrayList<>();
if(root == null) return ans;
Deque<TreeNode> d = new ArrayDeque<>();
while(!d.isEmpty() || root != null){
if(root != null){
d.addLast(root); // 将当前结点存入栈中
root = root.left; // 往左子树方向探 左
}else{ // 左边到尽头处了
TreeNode temp = d.pollLast();
ans.add(temp.val); // 中
root = temp.right; // 右
}
}
return ans;
}
}
LeetCode559. N 叉树的最大深度
题源 👉 559. N 叉树的最大深度
题目描述
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示,每组子节点由空值分隔(请参见示例)。
示例:
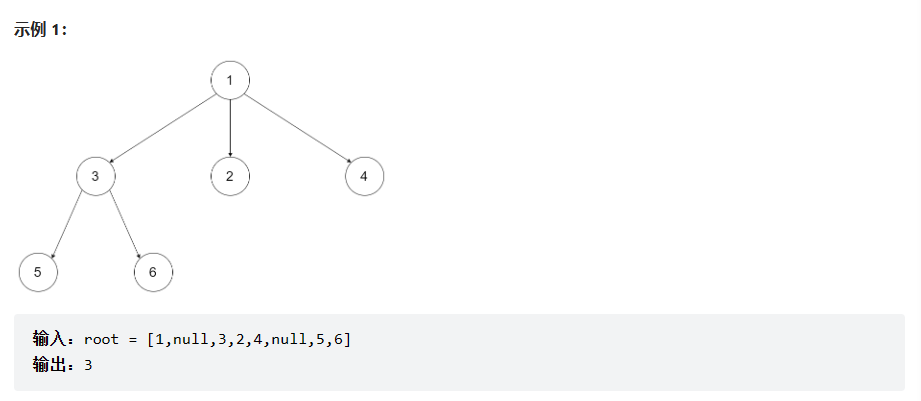
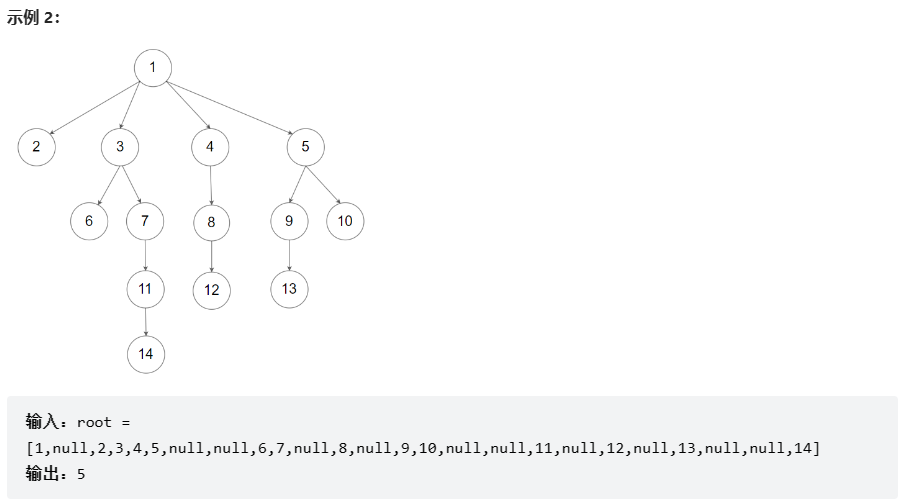
提示:
- 树的深度不会超过
1000。- 树的节点数目位于
[0, 104]之间。
思路及实现
方法一:DFS
具体实现:
class Solution {
public int maxDepth(Node root) {
if(root == null) return 0;
int ans = 0;
for(Node node : root.children){
ans = Math.max(ans, maxDepth(node)); // 求当前结点各子树最大深度
}
// 加上当前结点的一个深度
// 即从当前结点出发的最大深度
return ans + 1;
}
}
时间复杂度:O(n)
空间复杂度:O(h),h为深度
方法二:BFS
相当于多叉树的层次遍历。
多叉树的层数即最大深度。
具体实现:
class Solution {
public int maxDepth(Node root) {
if(root == null) return 0;
int ans = 0;
Deque<Node> d = new ArrayDeque<>();
d.addLast(root);
while(!d.isEmpty()){
int size = d.size(); // 一层结点数
while(size-- > 0){ // 遍历该层结点
Node t = d.pollFirst(); // 取出当前层结点
for(Node node : t.children) // 将结点的子结点入队
d.addLast(node);
}
ans++; // 层数(深度)+ 1
}
return ans;
}
}
时间复杂度:O(n)
空间复杂度:O(n)
LeetCode589. N 叉树的前序遍历
题源 👉 589. N 叉树的前序遍历
## 题目描述
给定一个 n 叉树的根节点 root ,返回 其节点值的 前序遍历 。
n 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。
示例:
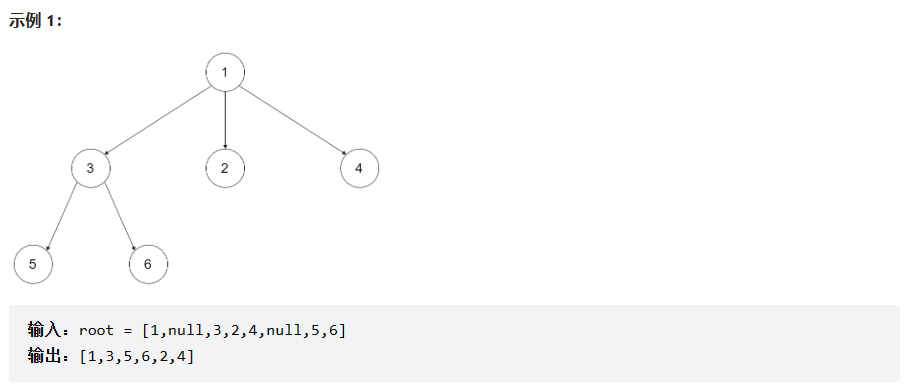
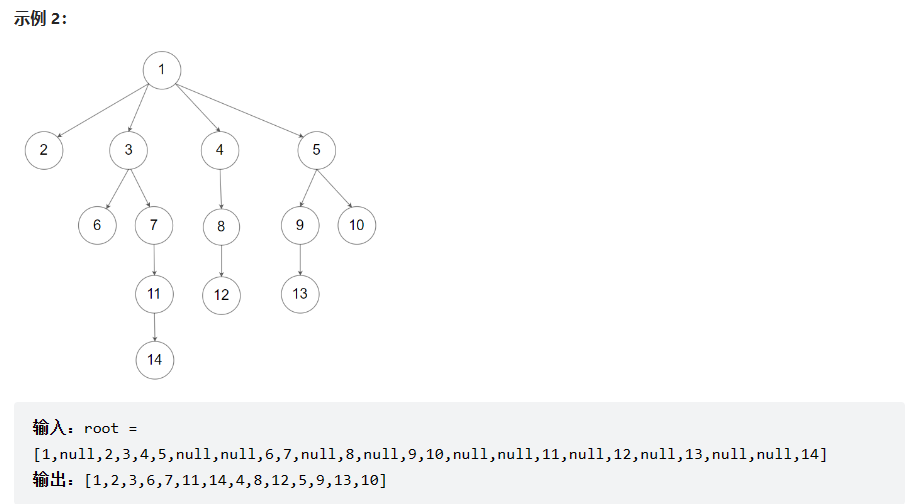
提示:
- 节点总数在范围
[0, 104]内0 <= Node.val <= 104- n 叉树的高度小于或等于
1000
思路及实现
方法一:递归
具体实现:
class Solution {
List<Integer> ans = new ArrayList<>();
public List<Integer> preorder(Node root){
dfs(root);
return ans;
}
public void dfs(Node root){
if(root == null) return;
ans.add(root.val);
for(Node node : root.children)
dfs(node);
}
}
方法二:迭代
具体实现:
class Solution {
public List<Integer> preorder(Node root){
List<Integer> ans = new ArrayList<>();
if(root == null) return ans;
Deque<Object[]> d = new ArrayDeque<>(); // 使用栈进行前序遍历
d.addLast(new Object[]{root, 0}); // 存入当前结点,及当前结点遍历过的子结点数
while(!d.isEmpty()){
Object[] p = d.pollLast();
Node t = (Node)p[0]; Integer cnt = (Integer)p[1];
if(t == null) continue;
if(cnt == 0) ans.add(t.val); // 前序遍历,将根值存入
if(cnt < t.children.size()){ // 当前结点遍历过的子结点数<当前结点子结点数
d.addLast(new Object[]{t, cnt+1}); // 再次将当前结点入栈
d.addLast(new Object[]{t.children.get(cnt), 0}); // 当前结点的第cnt+1个子结点入栈
}
}
return ans;
}
}
LeetCode590. N 叉树的后序遍历
题源 👉 590. N 叉树的后序遍历
## 题目描述
给定一个 n 叉树的根节点 root ,返回 其节点值的 后序遍历 。
n 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。
示例:
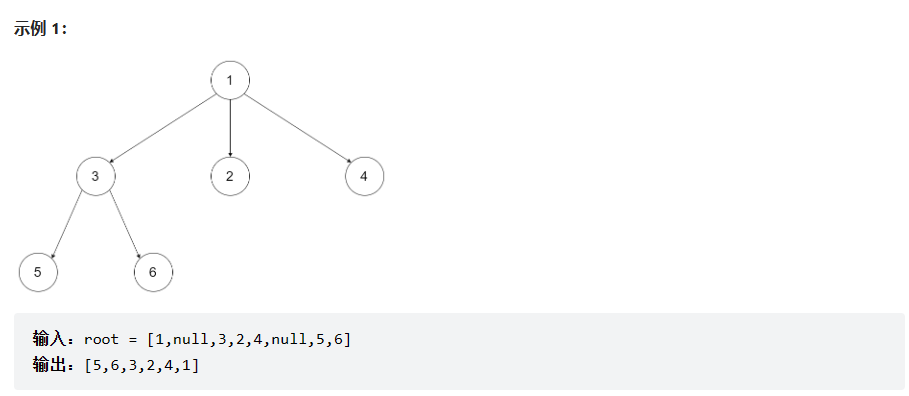
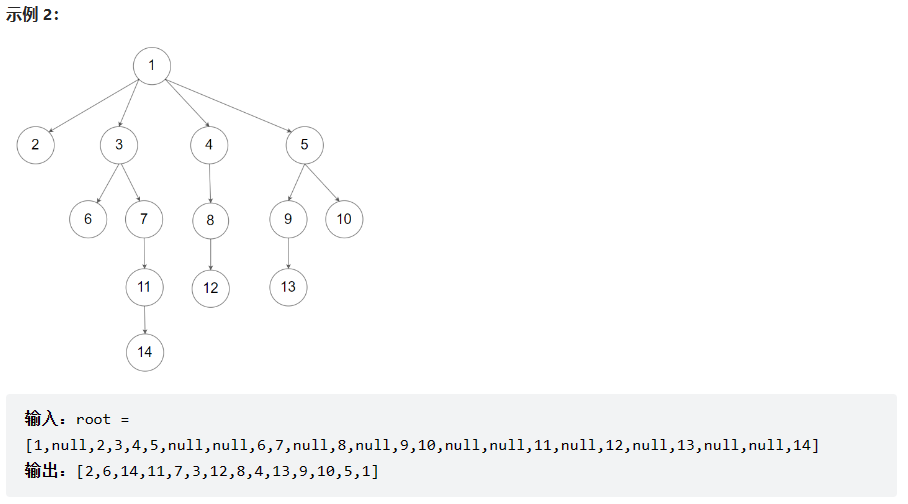
提示:
- 节点总数在范围
[0, 104]内0 <= Node.val <= 104- n 叉树的高度小于或等于
1000
思路及实现
方法一:递归
具体实现:
class Solution {
List<Integer> ans = new ArrayList<>();
public List<Integer> postorder(Node root) {
dfs(root);
return ans;
}
public void dfs(Node root){
if(root == null) return;
for(Node node : root.children)
dfs(node);
ans.add(root.val);
}
}
方法二:迭代
class Solution {
public List<Integer> postorder(Node root) {
List<Integer> ans = new ArrayList<>();
if(root == null) return ans;
Deque<Object[]> d = new ArrayDeque<>();
d.addLast(new Object[]{root, 0});
while(!d.isEmpty()){
Object[] p = d.pollLast();
Node t = (Node)p[0]; Integer cnt = (Integer)p[1];
if(t == null) continue;
if(cnt == t.children.size()) ans.add(t.val);
if(cnt < t.children.size()){
d.addLast(new Object[]{t, cnt + 1});
d.addLast(new Object[]{t.children.get(cnt), 0});
}
}
return ans;
}
}








![[强网杯 2019]随便注](https://img-blog.csdnimg.cn/af45b93cd5da43ef8ff837ead73ef514.png)