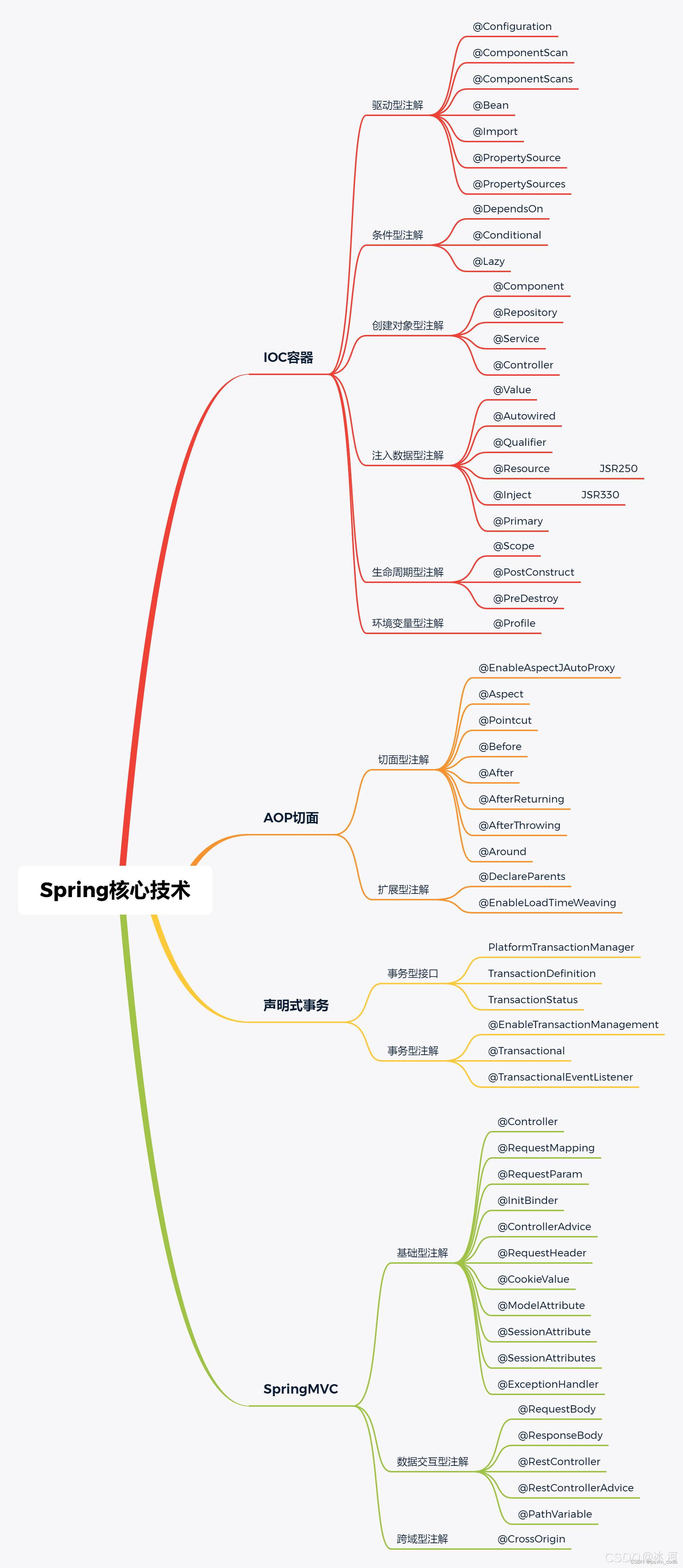
随机森林模型的基本原理和代码实现
集成模型简介
集成学习模型是机器学习非常重要的一部分。
集成学习是使用一系列的弱学习器(或称之为基础模型)进行学习,并将各个弱学习器的结果进行整合从而获得比单个学习器更好的学习效果的一种机器学习方法。
集成学习模型有两种常见的算法:
- Bagging算法的典型机器学习模型为本次的随机森林模型
- Boosting算法的典型机器学习模型为之后的AdaBoost、GBDT、XGBoost和LightGBM模型。
随机森林模型的基本原理
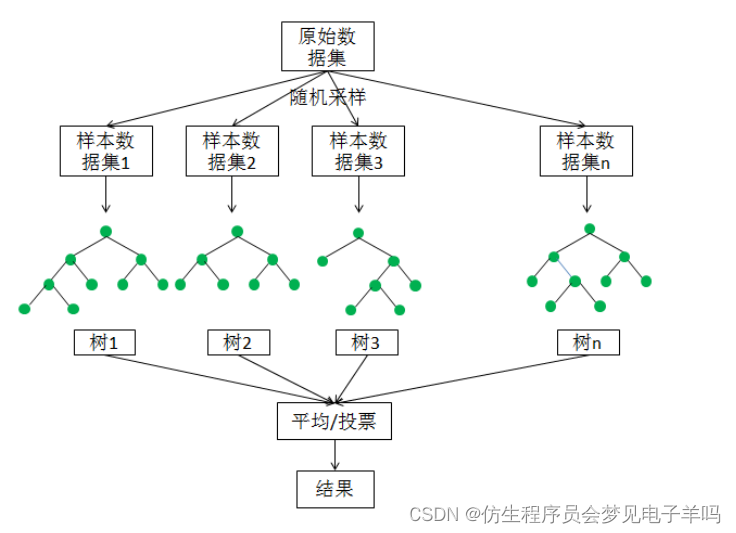
如下如所示,随机森林模型会在原始数据集中随机抽样,构成n个不同的样本数据集,然后根据这些数据集搭建n个不同的决策树模型,最后根据这些决策树模型的平均值(针对回归模型)或者投票(针对分类模型)情况来获取最终结果。
为了保证模型的泛化能力,随机森林在建立每棵树的时候,往往会遵循两个基本原则:
- 数据随机:随机地从所有数据中有放回地抽取数据作为其中一棵决策树的数据进行训练。举例来说,有1000个原始数据,有放回地抽取1000次,构成一组新的数据(因为是有放回抽取,有些数据可能被选中多次,有些数据可能不被选上),作为某一个决策树的数据来进行模型的训练。
- 特征随机:如果每个样本的特征维度为M,指定一个常数k<M,随机地从M个特征中选取k个特征,在使用Python构造随机森林模型时,默认取特征的个数k是M的平方根: M \sqrt M M
随机森林和决策树模型一样,可以做分类分析,也可以做回归分析。
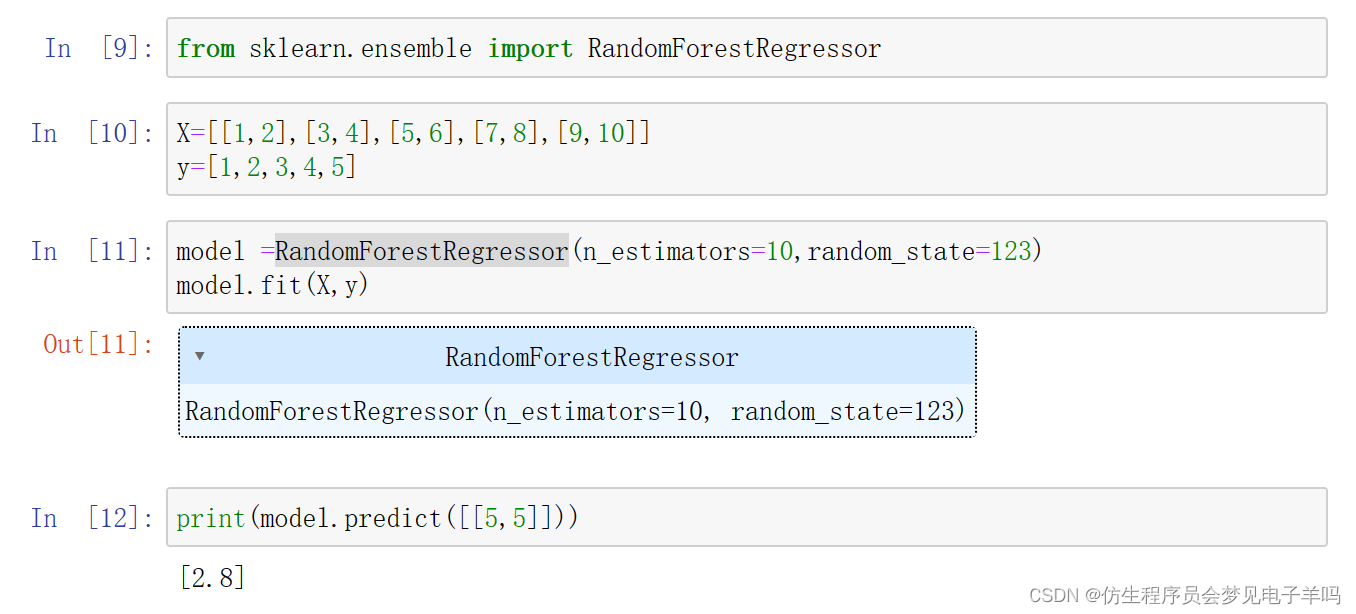
代码实现
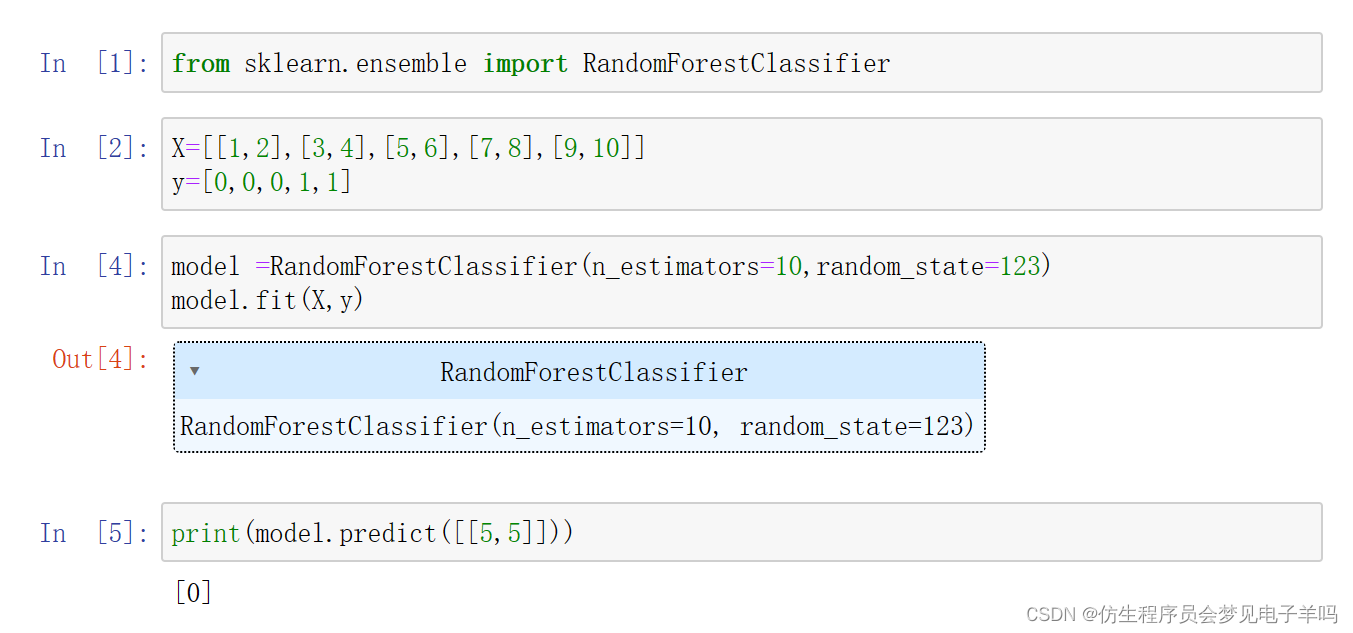
随机森林分类模型:
随机森林回归模型:
量化金融-股票数据获取
tushare库基本介绍
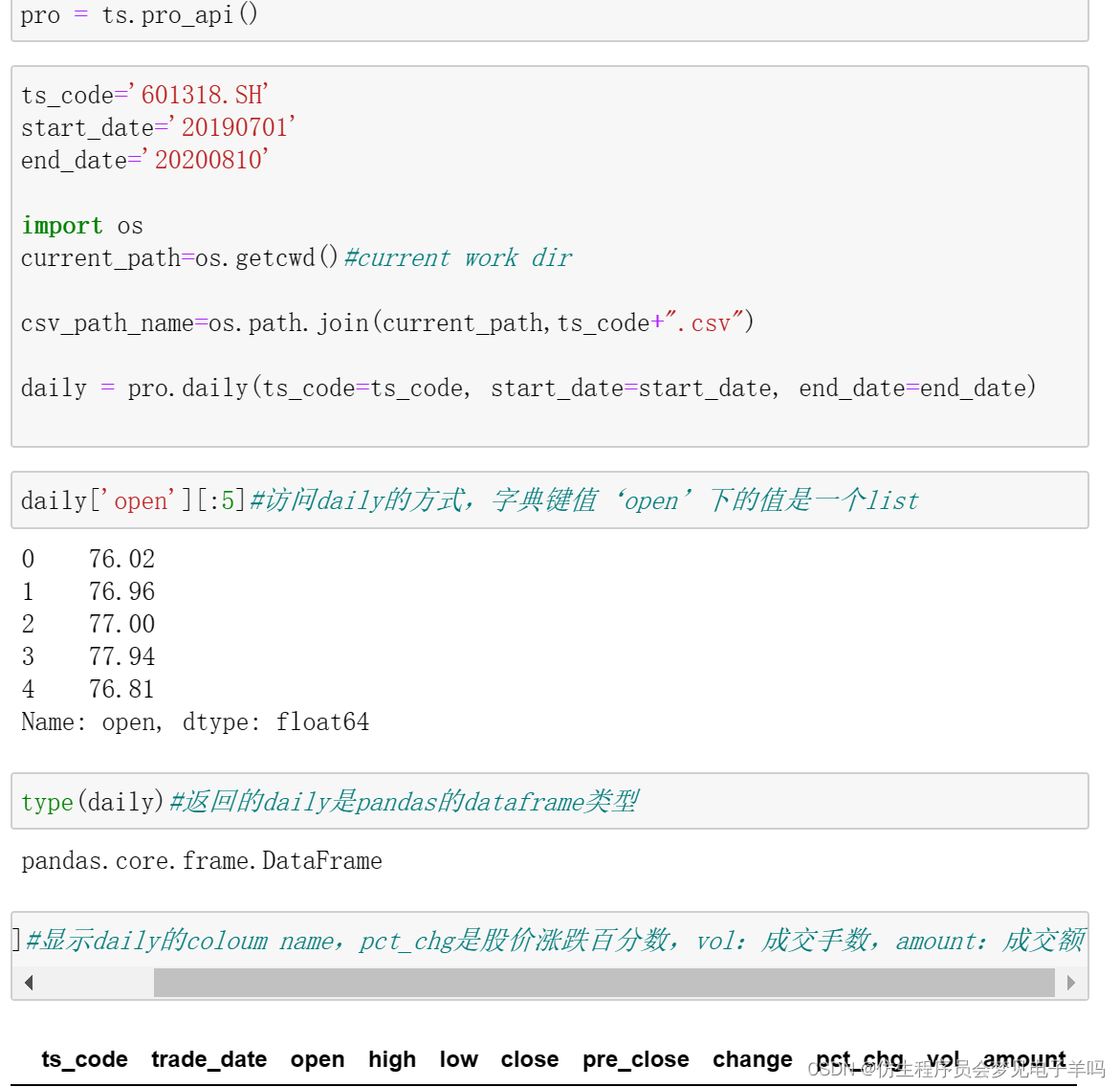
通过日期取历史某一天的全部历史
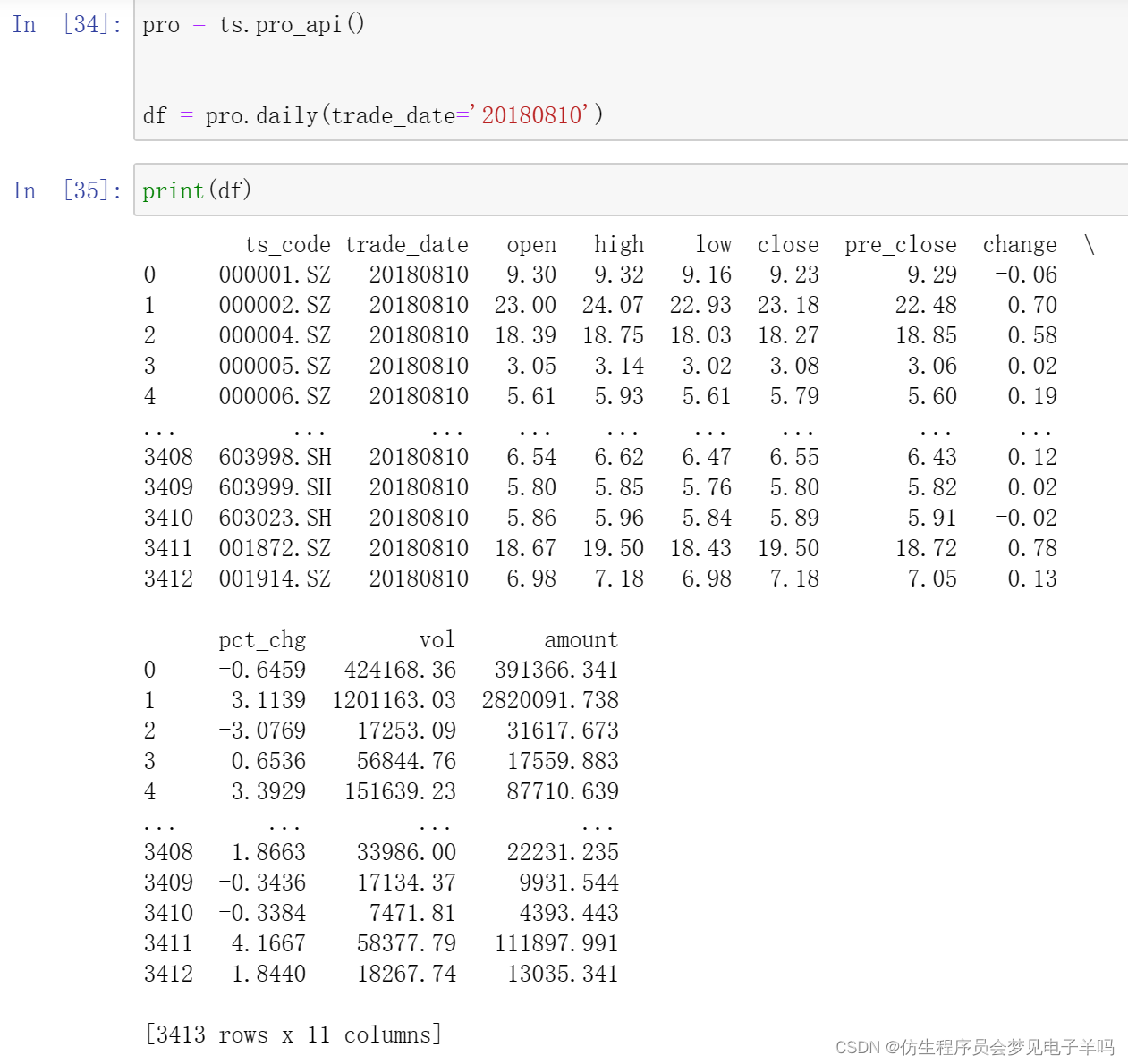
单只股票某日:
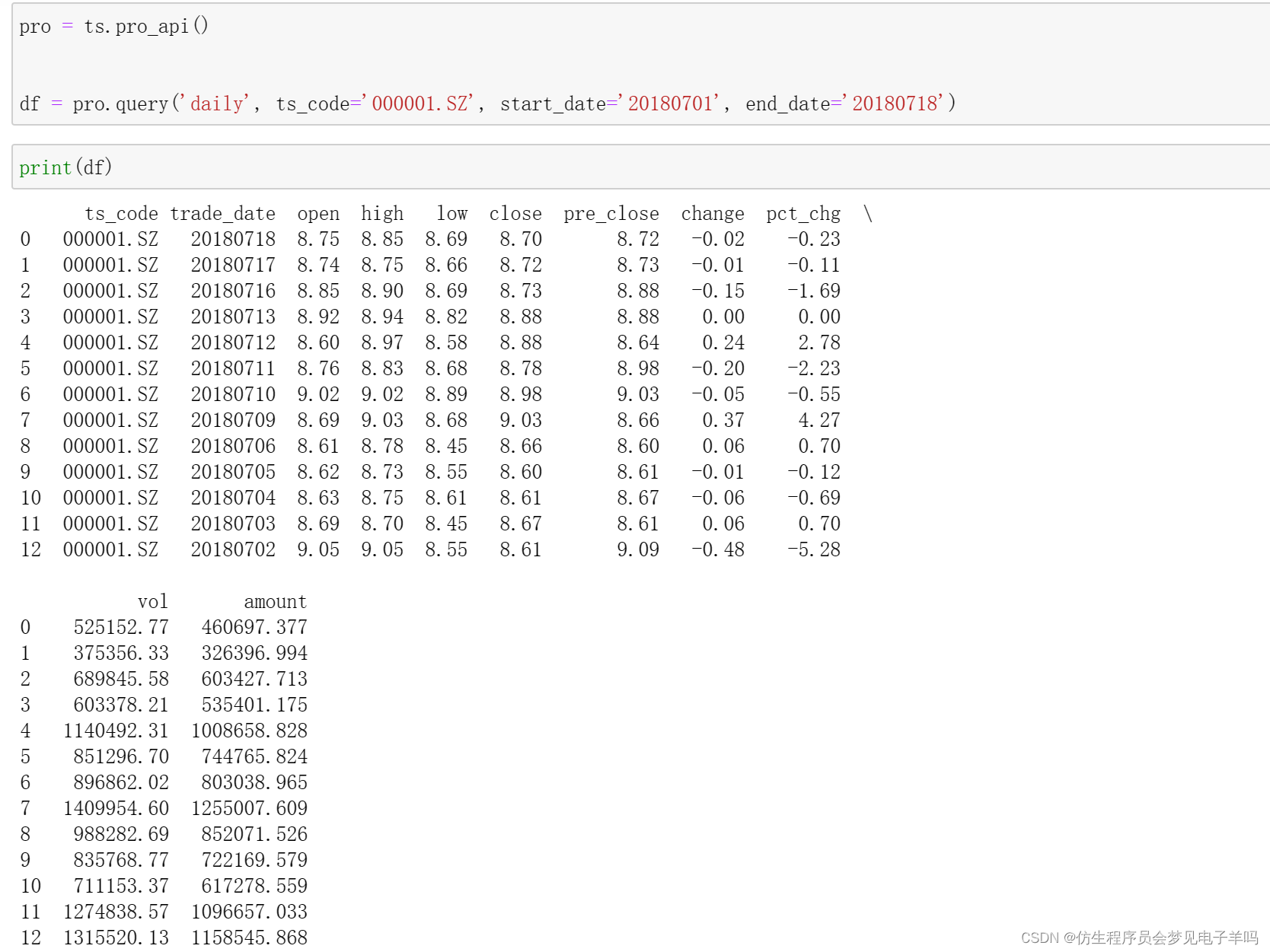
#多个股票
df = pro.daily(ts_code='000001.SZ,600000.SH', start_date='20180701', end_date='20180718')
ts_code trade_date open high low close pre_close change pct_chg \
0 600000.SH 20180718 9.51 9.64 9.48 9.51 9.44 0.07 0.74
1 000001.SZ 20180718 8.75 8.85 8.69 8.70 8.72 -0.02 -0.23
2 000001.SZ 20180717 8.74 8.75 8.66 8.72 8.73 -0.01 -0.11
3 600000.SH 20180717 9.41 9.48 9.38 9.44 9.41 0.03 0.32
4 000001.SZ 20180716 8.85 8.90 8.69 8.73 8.88 -0.15 -1.69
5 600000.SH 20180716 9.50 9.54 9.34 9.41 9.49 -0.08 -0.84
6 600000.SH 20180713 9.57 9.58 9.46 9.49 9.47 0.02 0.21
7 000001.SZ 20180713 8.92 8.94 8.82 8.88 8.88 0.00 0.00
8 000001.SZ 20180712 8.60 8.97 8.58 8.88 8.64 0.24 2.78
9 600000.SH 20180712 9.41 9.61 9.39 9.57 9.38 0.19 2.03
10 000001.SZ 20180711 8.76 8.83 8.68 8.78 8.98 -0.20 -2.23
11 600000.SH 20180711 9.37 9.44 9.32 9.38 9.57 -0.19 -1.99
12 000001.SZ 20180710 9.02 9.02 8.89 8.98 9.03 -0.05 -0.55
13 600000.SH 20180710 9.61 9.65 9.50 9.57 9.60 -0.03 -0.31
14 000001.SZ 20180709 8.69 9.03 8.68 9.03 8.66 0.37 4.27
15 600000.SH 20180709 9.37 9.63 9.37 9.60 9.37 0.23 2.45
16 600000.SH 20180706 9.31 9.43 9.17 9.37 9.26 0.11 1.19
17 000001.SZ 20180706 8.61 8.78 8.45 8.66 8.60 0.06 0.70
18 600000.SH 20180705 9.26 9.35 9.22 9.26 9.31 -0.05 -0.54
19 000001.SZ 20180705 8.62 8.73 8.55 8.60 8.61 -0.01 -0.12
20 600000.SH 20180704 9.34 9.42 9.28 9.31 9.35 -0.04 -0.43
21 000001.SZ 20180704 8.63 8.75 8.61 8.61 8.67 -0.06 -0.69
22 000001.SZ 20180703 8.69 8.70 8.45 8.67 8.61 0.06 0.70
23 600000.SH 20180703 9.29 9.38 9.20 9.35 9.29 0.06 0.65
24 600000.SH 20180702 9.55 9.55 9.23 9.29 9.56 -0.27 -2.82
25 000001.SZ 20180702 9.05 9.05 8.55 8.61 9.09 -0.48 -5.28
vol amount
0 189227.00 180858.003
1 525152.77 460697.377
2 375356.33 326396.994
3 137134.95 129512.091
4 689845.58 603427.713
5 144141.19 135697.106
6 150263.39 142708.347
7 603378.21 535401.175
8 1140492.31 1008658.828
9 197048.37 188206.858
10 851296.70 744765.824
11 152039.33 142450.919
12 896862.02 803038.965
13 124028.37 118668.133
14 1409954.60 1255007.609
15 221725.65 212109.327
16 225944.43 210564.106
17 988282.69 852071.526
18 164954.38 152978.661
19 835768.77 722169.579
20 144647.77 135000.876
21 711153.37 617278.559
22 1274838.57 1096657.033
23 241235.51 224816.757
24 226690.89 212743.905
25 1315520.13 1158545.868
股票衍生变量生成
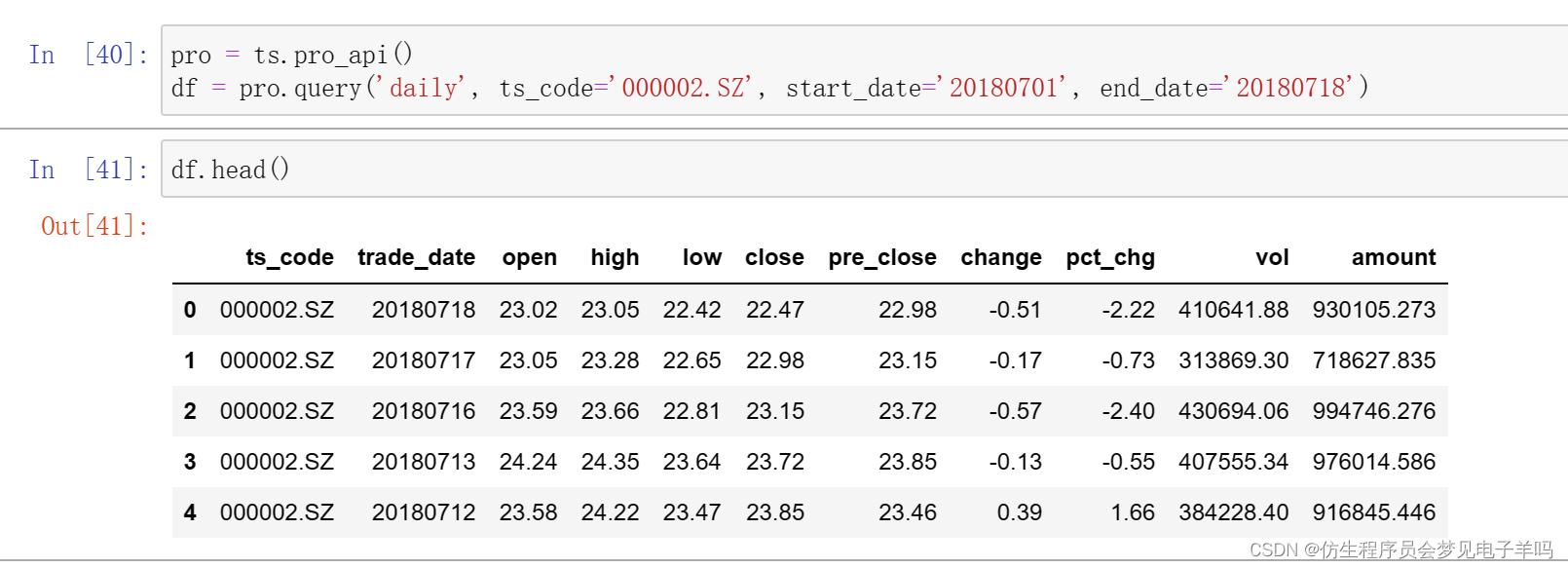
pro = ts.pro_api()
df = pro.query('daily', ts_code='000002.SZ', start_date='20180701', end_date='20180718')
简单衍生变量的计算:

通过如下代码可以先构造一些简单的衍生变量:
df['close-open']=(df['close']-df['open'])/df['open']
df['high-low']=(df['high']-df['low'])/df['low']
df['pre_close']=df['close'].shift(1)#该列所以往下移一行形成昨日收盘价
df['price-change']=(df['close']-df['pre_close'])
df['p_change']=(df['close']-df['pre_close'])/df['pre_close']*100
股票衍生变量生成
移动平均线指标MA值
通过如下代码可以获得股价5日移动平均值和10日移动平均值:
df['MA5']=df['close'].rolling(5).mean()
df['MA10']=df['close'].rolling(10).mean()
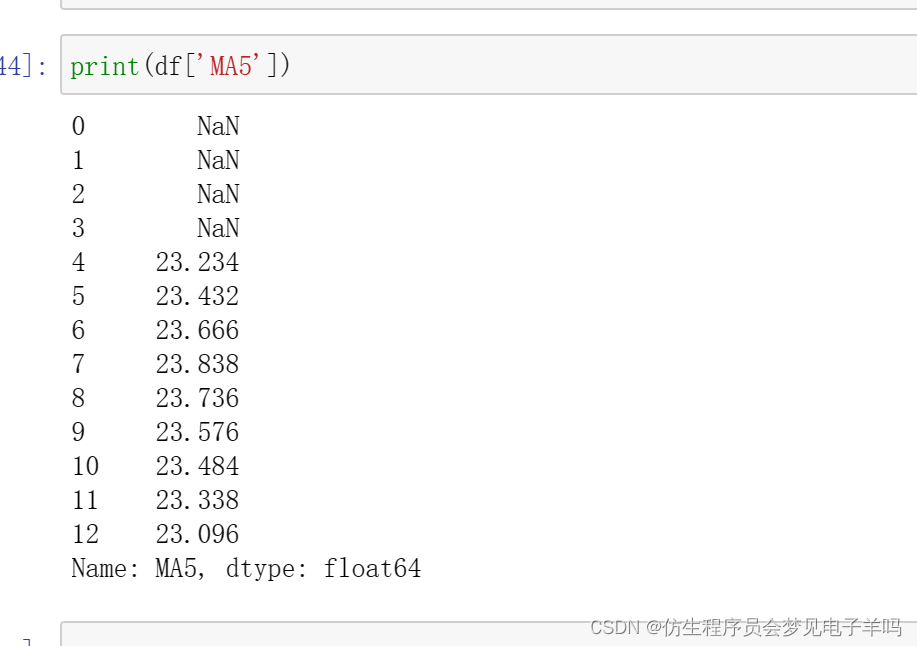
由于当我们在计算像MA5这样的数据时,数据前四天对应的平均值是无法计算出来的(因为最开始四天数据量不够去计算5日均值),所以会产生空值,通常会通过dropna()函数删除空值,以免在后续计算中出现空值造成的问题。
代码如下:
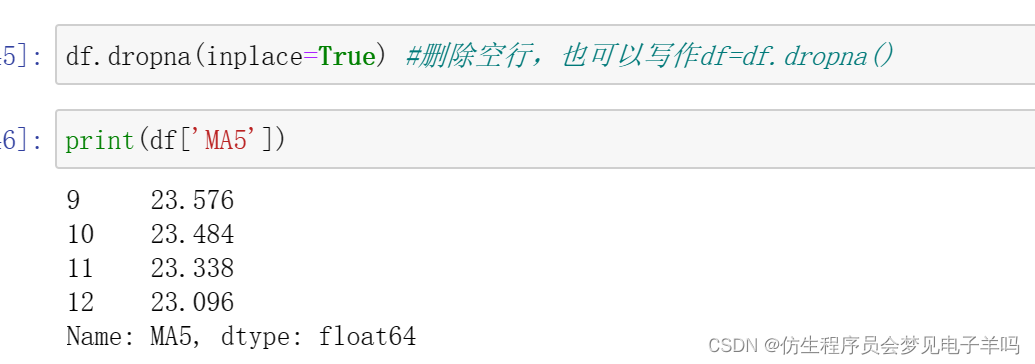
df.dropna(inplace=True) #删除空行,也可以写作df=df.dropna()



![[强网杯 2019]随便注](https://img-blog.csdnimg.cn/af45b93cd5da43ef8ff837ead73ef514.png)