数据结构与算法4

数据结构与算法4—队列

news2024/12/23 23:21:14

队列

队列的定义

队列(Queue)也是一种运算受限的线性表。它只允许在表的一端进行插入，而在另一端进行删除。允许删除的一端称为队头(front)，允许插入的一端称为队尾(rear)。
队列的修改是依先进先出的原则进行的。

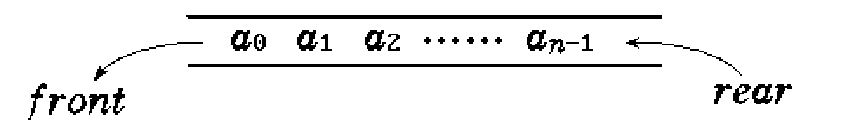
队列的基本操作

1．初始化队列 InitQueue(&Q) 将队列Q设置成一个空队列。

2．入队列 EnQueue(&Q,X) 将元素X插入到队尾中，也称“进队” ，“插入”。

3．出队列 OutQueue(&Q,&e) 将队列Q的队头元素删除，并用e返回其值，也称“退队”、“删除”。

4．取队头元素 GetHead(Q,&e) 得到队列Q的队头元素之值，并用e返回其值。 5．判队空 QueueEmpty(Q) 判断队列Q是否为空，若为空返回1，否则返回0。

队列的顺序实现

在非空队列里，头指针始终指向队头元素，而尾指针始终指向队尾元素的下一位置。

#define MaxSize  100
typedef int DataType;
typedef struct{
   DataType data[MaxSize];
   int front,rear;
 }Queue;

顺序队列（ MaxSize=4 ）的几种状态：

（1）表示空队列， rear==front==0。（4）A出队后，rear==front==3。再插入元素时，会出现假溢出的情况。

克服假溢出的方法：

（1）将队列中的所有元素均向最前端的位置移动；

（2）采用循环队列。

循环队列

循环队列的物理存储未发生任何改变，其只是充分利用数组空间，想象将数组的首尾连接起来，形成一个循环队列。

（a）表示空队列， rear==front==0。

（b）元素A入队后， rear==1， front==0。

（c）B，C依次入队后， rear==3， front==0。

（d）A,B,C出队后, front==3 ,rear==3。队列又为空

所以，循环队列为空的判定条件为：front==rear;

基本实现

#include"stdio.h"
#include"stdlib.h"

#define Maxsize 100
typedef int DataType;

typedef struct {
    DataType data[Maxsize];
    int front,rear;
}Queue;

//初始化队列
void InitQueue(Queue *Q)
{
    Q->front=Q->rear=0;
}
//入队
int InQueue(Queue *Q,DataType x)
{
    if((Q->rear+1)%Maxsize==Q->front)
        return 0;
    Q->rear=(Q->rear+1)%Maxsize; //if (Q->rear+1)==Maxsize,Q->rear=0
    Q->data[Q->rear]=x;
    return 1;
}
//判断空队列
int EmptyQueue(Queue *Q)
{
    if(Q->rear==Q->front)
        return 1;
    else
        return 0;
}
//出队
int OutQueue(Queue *Q,DataType *x)
{
    if(EmptyQueue(Q))
        return 0;
    Q->front=(Q->front+1)%Maxsize;
    *x=Q->data[Q->front];
    return 1;
}
//取队头元素
int GetHead(Queue *pQ,DataType *px)
{ 
    if(EmptyQueue(pQ))
      {    printf("\n Queue is free");
            return 0;
      }
      *px=pQ->data[(pQ->front+1)%MaxSize];
          return 1;
}

循环队列中的常用判断语句

（1）队列判空条件：rear==front;

（2）队列判满条件：(rear+1)%MaxSize==front;

（3）入队操作：

第①步，先判断队列是否已满；

第②步，rear=(rear+1)%MaxSize；

第③步：尾指针位置赋值相应元素；

（4）出队操作：

第①步，先判断队列是否已空；

第②步，front=(front+1)%MaxSize；

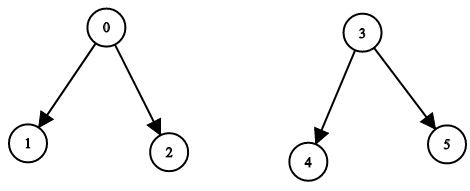
（5）计算循环队列中元素的个数：分两种情况讨论，如图所示：

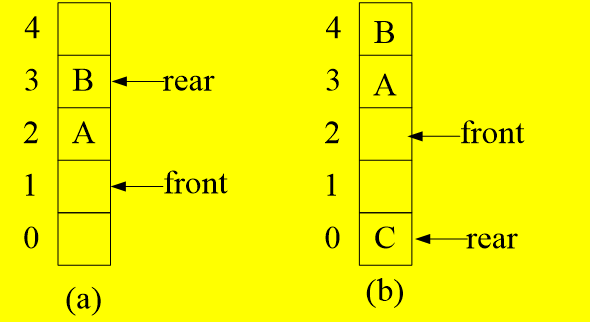
所以：(rear-front+MaxSize)%MaxSize。

队列的链式表示和实现

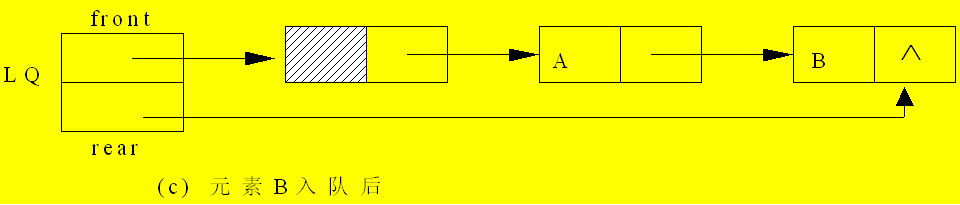
队列的链式存储结构简称为链队。它实际上是一个同时带有首指针和尾指针的单链表。头指针指向表头结点，而尾指针则指向队尾元素。

链队结构示意图：

链队的数据类型定义如下：

typedef int DataType;
typedef struct qnode{
    DataType data;
    struct qnode *next;
}Qtype;
typedef struct qptr{
    Qtype *front,*rear;
}LinkQueue;
LinkQueue LQ;

链队运算指针变化情况：

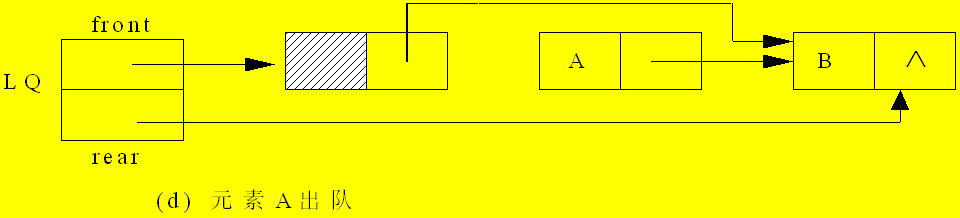
c语言实现：

#include"stdio.h"
#include"malloc.h"
typedef int DataType; //定义队列类型
//定义队结点
typedef struct node
{
    DataType data;
    struct node *next;
}qnode; //链队结点类型
 
typedef struct
{
    qnode *front; //定义qnode *类型的指针成员
    qnode *rear;
}LinkQueue;
 
//初始化队
int InitQueue(LinkQueue *Q)
{
    Q->front=Q->rear=(qnode *)malloc(sizeof(qnode)); //申请空间作头结点，头结点不存放数据
    if(!Q->front)  //if Q->front NULL
        return 0;
    Q->front->next=NULL; //使队头结点的指针域为NULL
    return 1;
}
//判断队空
int EmptyQueue(LinkQueue *Q)
{
    if(Q->front==Q->rear)
        return 1;
    else
        return 0;
}
//进队
void InQueue(LinkQueue *Q,DataType x)
{
    qnode *s;
    s=(qnode *)malloc(sizeof(qnode)); //申请一结点空间
    s->data=x;
    s->next=NULL; 
    Q->rear->next=s; //使s结点连上前一个结点
    Q->rear=s;  //尾指针指向结点，即最后一个结点
}
//出队
int OutQueue(LinkQueue *Q,DataType *e)
{
    qnode *q;
    if(EmptyQueue(Q))
        return 0;
    q=Q->front->next; //取头结点地址
    *e=q->data;  //返回头结点数据
    Q->front->next=q->next;  //头结点指针域存原第二结点地址
     if(Q->rear==q)  //if(Q->front->next==NULL) 若队列中只有1个元素，则出队后队列为空
         Q->rear=Q->front; 
     free(q); //释放q指向的结点，即队头结点 
    return 1;
}

队列的应用：