代码随想录算法训练营第48天|198.打家劫舍|213.打家劫舍II| 337.打家劫舍III

今天就是打家劫舍的一天，这个系列不算难，大家可以一口气拿下。

198.打家劫舍

视频讲解：https://www.bilibili.com/video/BV1Te411N7SX
https://programmercarl.com/0198.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8D.html

class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size()==0) return 0;
        if(nums.size()==1) return nums[0];
        vector<int> dp(nums.size());
        dp[0]=nums[0];
        dp[1]=max(nums[0],nums[1]);

        for(int i=2;i<nums.size();i++)
        {
            dp[i]=max(dp[i-2]+nums[i],dp[i-1]);
        }
        return dp[nums.size()-1];
    }
};

总结
比背包问题好理解，就是对先前的元素进行比较，最后得出最优。

213.打家劫舍II

视频讲解：https://www.bilibili.com/video/BV1oM411B7xq
https://programmercarl.com/0213.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8DII.html

class Solution {
public:
// 注意注释中的情况二情况三，以及把198.打家劫舍的代码抽离出来了
    int rob(vector<int>& nums) {
        if(nums.size()==0) return 0;
        if(nums.size()==1) return nums[0];

        int result1=robrange(nums,0,nums.size()-2); // 情况二
        int result2=robrange(nums,1,nums.size()-1); // 情况三

        return max(result1,result2);
    }
    // 198.打家劫舍的逻辑
    int robrange(vector<int>& nums,int start,int end)
    {
        if(end==start) return nums[start];
        vector<int>dp(nums.size());
        dp[start]=nums[start];
        dp[start+1]=max(nums[start],nums[start+1]);

        for(int i=start+2;i<=end;i++)
        {
            dp[i]=max(dp[i-2]+nums[i],dp[i-1]);
        }

        return dp[end];

    }
};

总结
同理上题，但是从环变情况，要考虑3种情况，最后精简到2种，

最后还是套打家劫舍的算法。

** 337.打家劫舍III**

视频讲解：https://www.bilibili.com/video/BV1H24y1Q7sY
https://programmercarl.com/0337.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8DIII.html

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int rob(TreeNode* root) {
        vector<int> result=robtree(root);
        return max(result[0],result[1]);
    }
    // 长度为2的数组，0：不偷，1：偷
    vector<int> robtree(TreeNode *cur)
    {
        if(cur==NULL) return vector<int> {0,0};
        vector<int>left=robtree(cur->left);
        vector<int>right=robtree(cur->right);
        // 偷cur，那么就不能偷左右节点。
        int val1=cur->val+left[0]+right[0];
        // 不偷cur，那么可以偷也可以不偷左右节点，则取较大的情况
        int val2=max(left[0],left[1])+max(right[0],right[1]);

        return {val2,val1};//返回的数据一定要小心
    }
};

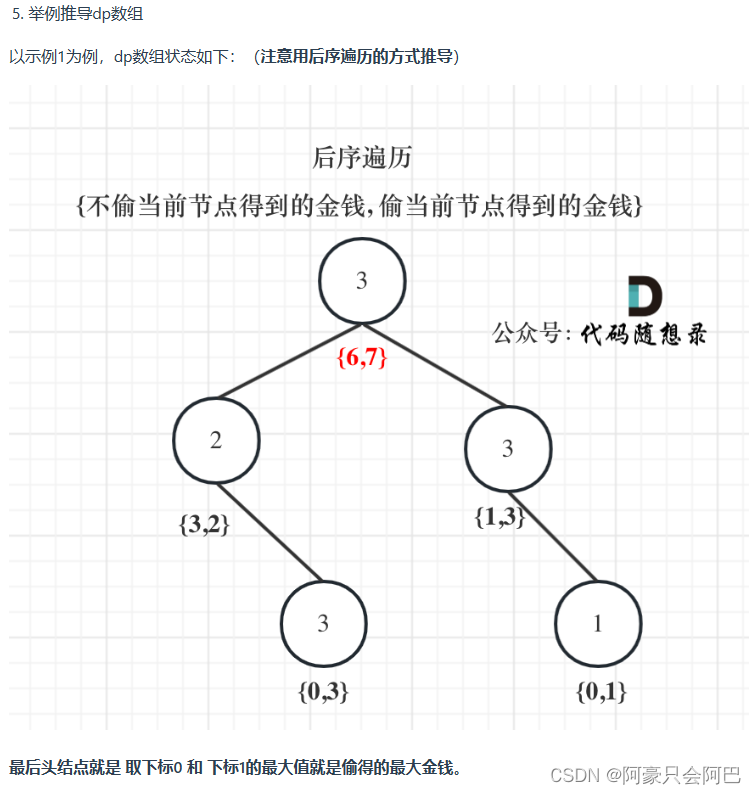
总结
是树与动态规划的结合，再后序遍历的方面上套打家劫舍算法来解决这个问题。