题目
LCR 178. 训练计划 VI
教学过程中,教练示范一次,学员跟做三次。该过程被混乱剪辑后,记录于数组
actions,其中actions[i]表示做出该动作的人员编号。请返回教练的编号。
- 示例 1:
输入:
actions = [5, 7, 5, 5]
输出:7
- 示例 2:
输入:
actions = [12, 1, 6, 12, 6, 12, 6]
输出:1
- 提示:
节点总数 <= 10000
思考
- 不同于LCR177,这道题的数字出现的次数不是偶数次,所以不能用异或来解决
解法1——统计所有位上 “1” 出现的次数
- 可以观察到,非目标数字出现的次数是相同的,因此我们可以选择遍历整个数组,统计每个位上 1 出现的次数,然后这个次数对非目标数字的出现次数求余,如果那一位上有目标数字的 1,则求余后应该为 1,否则求余后应该为 0,此为解法1
class Solution {
public:
int trainingPlan(vector<int>& actions) {
vector<int> count(32, 0);
for(auto &ele:actions){
for(int i=31; i>=0; --i){
if(ele & 1) count[i]++;
ele>>=1;
}
}
int ans=0;
for(int i=0; i<32; ++i){
ans <<= 1;
ans += count[i]%3;
}
return ans;
}
};
解法2——有限状态自动机
思想来源于https://leetcode.cn/leetbook/read/illustration-of-algorithm/9hctss/,以下是个人对这个解法的笔记
- 解法1是比较容易想到的,但是有一个缺点,就是遍历数组时,每个数字都要进行 32 次统计,且最终统计完成后又要遍历统计结果进行答案的还原
- 能否有一种方式,可以在遍历数组的时候一次性记录完成,无需对每个数字进行 32 次统计,且最后也不需要进行答案的还原呢?
- 对数组中每个元素进行位操作?通过对一位数字的统计,直接扩展到 32 位数字一次性统计?
- 我们可以很简单的得出,当对数组中的一个数字的操作结束后,单独某一位上 1 的个数对 3 取余后只有 3种状态:0、1、2
- 0、1、2 应该如何记录呢,我们考虑使用 2 位二进制数进行记录,即00、01、10
- 但是我们的最终目的是通过位运算一次操作就得到本轮遍历到的数字的统计结果,所以我们不能简单的用连续的两位二进制数进行统计,而是使用两个 32 位数进行统计,ones记录00、01、10的第一位数,twos记录00、01、10的第二位数。即:
| 第一个32位数ones | 0 | 0 | 0 | 0 | …… | 0 | 1 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| 第二个32位数twos | 0 | 0 | 0 | 0 | …… | 0 | 0 | 1 | 0 |
| 表示(这轮遍历后的情况) | 0 | 0 | 0 | 0 | …… | 0 | 2 | 1 | 0 |
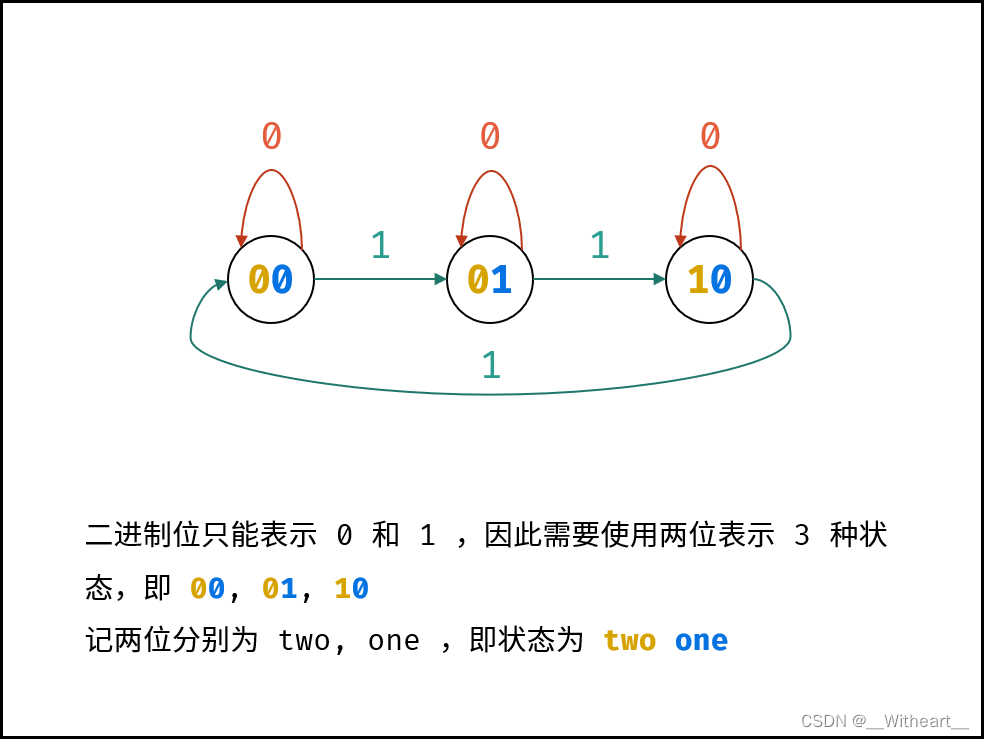
图片来自:https://leetcode.cn/leetbook/read/illustration-of-algorithm/9hctss/
- 知道了这个统计思想,那下一步就是思考选择什么样的位运算可以得到正确的结果
- 对ones有:
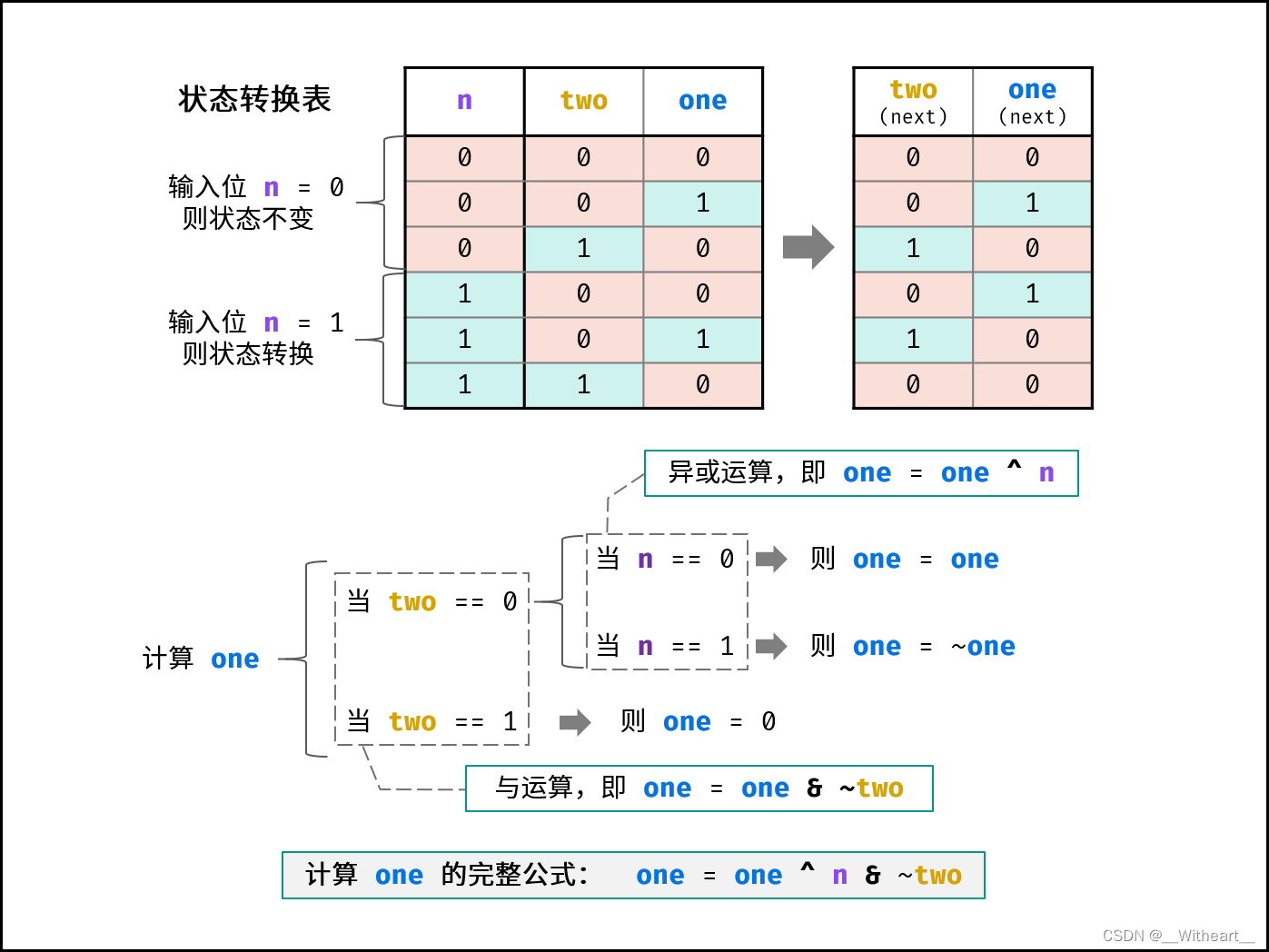
图片来自:https://leetcode.cn/leetbook/read/illustration-of-algorithm/9hctss/
这里有一个重点就是,当位运算出现了嵌套的条件,如当two满足什么,再n满足什么等等等等这种条件,可以使用 & 来保证其中一个条件的满足,而又不影响这个要去进一步判断是否 n 满足的这个数字的值,在这里就表现为
one = one & ~two;
在这样操作后,确保 one 已经满足了 two 这个条件,然后这个结果再去与 n 异或
one = one & ~two ^ n;
- 而 twos 的更新只需要注意当我们先更新 ones 后,twos 应该在新的 ones 上进行计算,选择位运算的方式同上
class Solution {
public:
// 计算训练计划
int trainingPlan(vector<int>& actions) {
// 初始化变量 ones 和 twos 为 0
int ones=0, twos=0;
// 对于 actions 中的每一个元素 ele
for(auto &ele:actions){
// 计算 ones 的状态转移
ones = ones ^ ele & ~twos; // 根据当前的 ele 更新 ones 的状态
// 计算 twos 的状态转移
twos = twos ^ ele & ~ones; // 根据当前的 ele 更新 twos 的状态
}
// 返回最终计算得到的 ones,它记录了“只出现一次的数字”的情况
return ones;
}
};