1多项式积分的解析解
本示例显示如何使用 polyint
函数对多项式求解析积分。使用此函数来计算多项式的不定积分。
1.1定义问题
考虑实数不定积分,

其中 k
是积分常量。由于没有指定积分限值,
integral
函数族不太适合求解这个问题。
1.2用向量表示多项式
创建一个向量,其元素代表各 x 降幂的系数。
p = [4 0 -2 0 1 4];1.3对多项式求解析积分
使用 polyint
函数求多项式的解析积分。指定第二输入参数的积分常量。
k = 2;
I = polyint(p,k)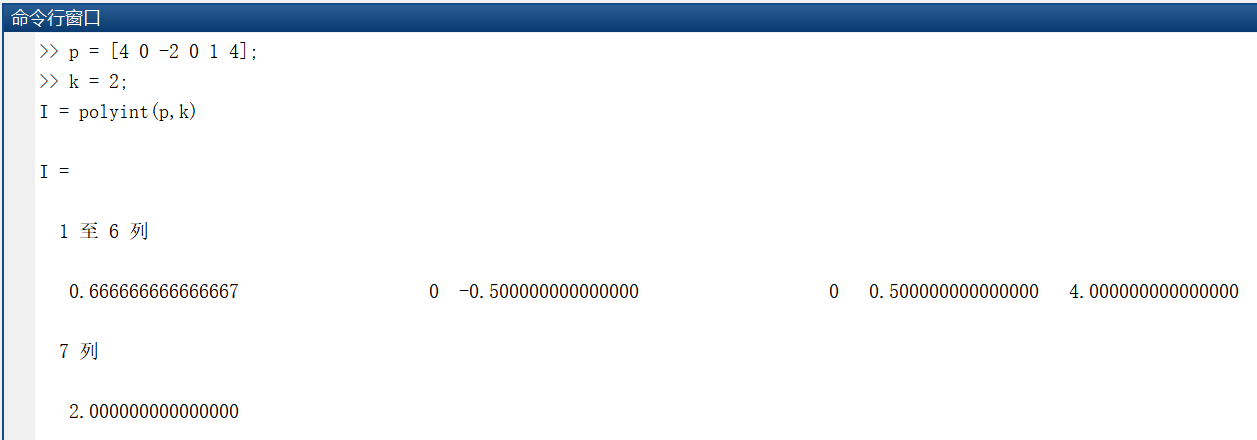
输出是一个 x 降幂系数向量。这一结果与上述解析解相匹配,但有积分常量
k = 2
。
2数值数据的积分
此示例显示如何对一组离散速度数据进行数值积分以逼近行驶距离。integral 族仅接受函数句柄输入,所以这些函数不能用于离散数据集。当函数表达式不能用于积分时,使用
trapz
或
cumtrapz
。
2.1查看速度数据
考虑以下速度数据和相应的时间数据。
vel = [0 .45 1.79 4.02 7.15 11.18 16.09 21.90 29.05 29.05 ...
29.05 29.05 29.05 22.42 17.9 17.9 17.9 17.9 14.34 11.01 ...
8.9 6.54 2.03 0.55 0];
time = 0:24;
这些数据代表汽车的速度(米/秒),间隔为 1 秒,时间超过 24 秒。
绘制速度数据点并将各点用直线连接。
figure
plot(time,vel,'-*')
grid on
title('Automobile Velocity')
xlabel('Time (s)')
ylabel('Velocity (m/s)')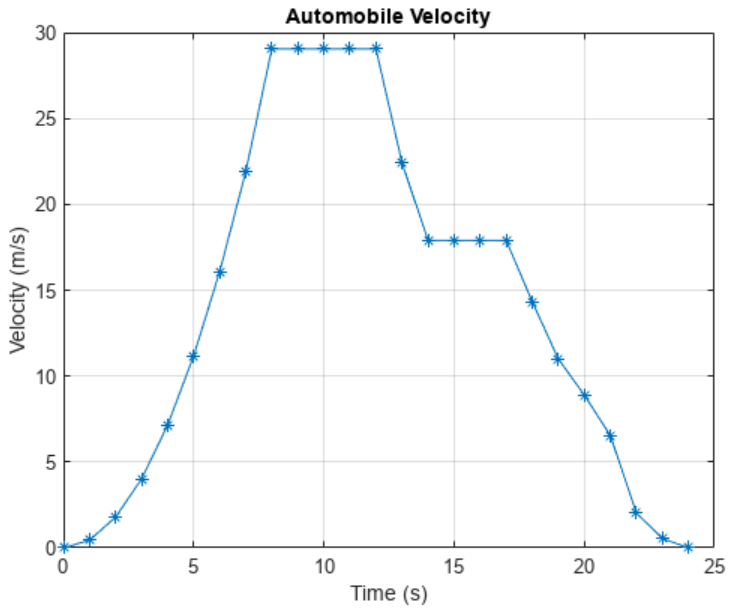
斜率在加速时为正,恒速时为零,减速时为负。在 t = 0
的时间点,车辆处于静止,速度为
vel(1) = 0 米/秒。然后车辆以
vel(9) = 29.05
米/秒的速度加速,并在
t = 8 秒内达到最大速度,并保持这种速度 4 秒的时间。然后车辆在 3 秒之内减速到
vel(14) = 17.9 米/秒并最终静止。由于这个速度曲线有多处不连续,此不能用单一连续函数来描述。

2.2计算总行驶距离
trapz 使用数据点进行离散积分以创建梯形,所以它非常适合处理不连续的数据集。这种方法假设在数据点之间为线性行为,当数据点之间的行为是非线性时,精度可能会降低。为了说明这一点,可将数据点作为顶点在图表上画出梯形。
xverts = [time(1:end-1); time(1:end-1); time(2:end); time(2:end)];
yverts = [zeros(1,24); vel(1:end-1); vel(2:end); zeros(1,24)];
p = patch(xverts,yverts,'b','LineWidth',1.5);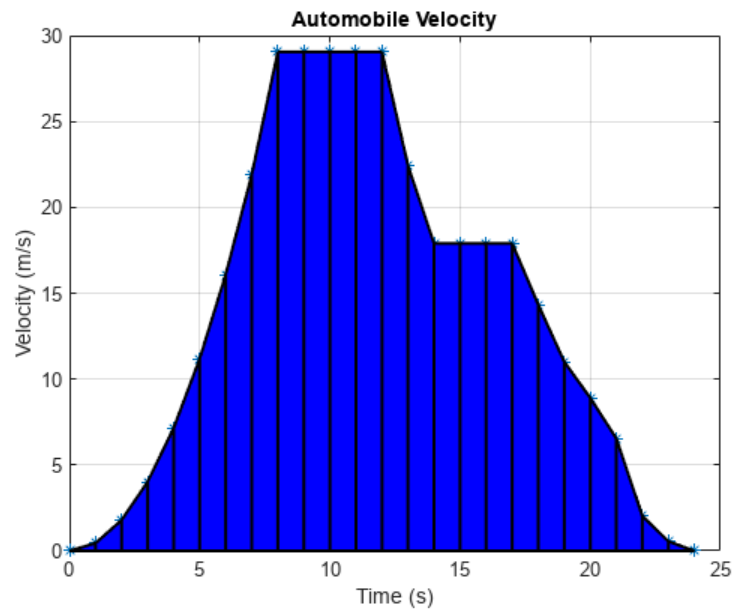
trapz 可通过将区域分解成梯形来计算离散数据集下的面积。然后,函数将每个梯形面积累加来计算总面积。
通过使用 trapz 求速度数据积分来计算汽车的总行驶距离(对应的着色区域)。默认情况下,如果使用语法
trapz(Y)
,则假定点之间的间距为
1
。但是,您可以使用语法
trapz(X,Y) 指定不同的均匀或非均匀间距
X
。在这种情况下,
time
向量中读数之间的间距是
1
,因此可以使用默认间距。
distance = trapz(vel)
distance = 345.2200
汽车在
t = 24
秒内行驶的距离约为 345.22 米。
2.3绘制累积行驶距离
cumtrapz 函数与
trapz
密切相关。
trapz
仅返回最终的积分值,而 cumtrapz 还在向量中返回中间值。计算累积行驶距离并绘制结果。
cdistance = cumtrapz(vel);
T = table(time',cdistance','VariableNames',{'Time','CumulativeDistance'})
结果为:
T=25×2 table
Time CumulativeDistance
____ __________________
0 0
1 0.225
2 1.345
3 4.25
4 9.835
5 19
6 32.635
7 51.63
8 77.105
9 106.15
10 135.2
11 164.25
12 193.31
13 219.04
14 239.2
15 257.1
plot(cdistance)
title('Cumulative Distance Traveled Per Second')
xlabel('Time (s)')
ylabel('Distance (m)')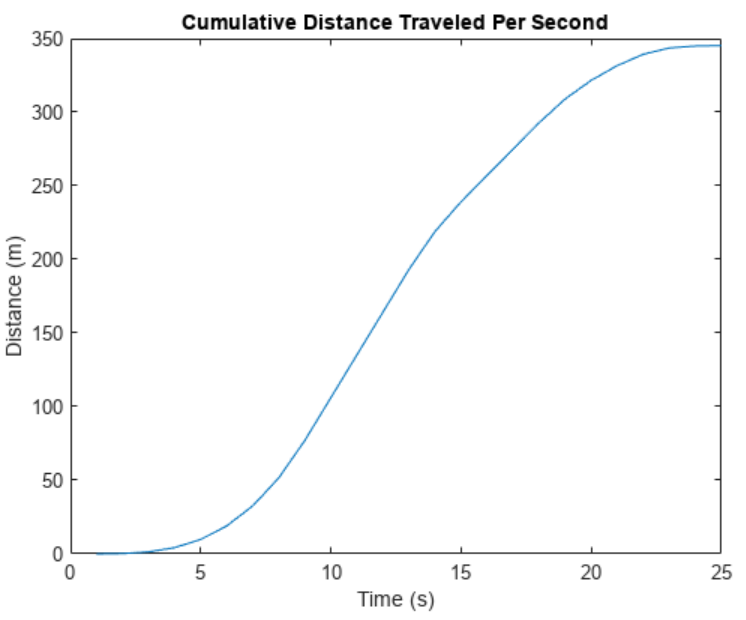
3计算表面的切平面
此示例说明如何按有限差分逼近函数梯度。然后说明如何通过使用这些逼近的梯度,绘制平面上某个点的切平面。
f = @(x,y) x.^2 + y.^2;
使用
gradient
函数,相对
x
和
y
逼近
f
(
x
,
y
)
的偏导数。选择与网格大小相同的有限差分长度。
[xx,yy] = meshgrid(-5:0.25:5);
[fx,fy] = gradient(f(xx,yy),0.25);
为逼近切平面
z
,您需要求取相关点的导数值。获取该点的索引,并求取该位置的近似导数。
x0 = 1;
y0 = 2;
t = (xx == x0) & (yy == y0);
indt = find(t);
fx0 = fx(indt);
fy0 = fy(indt);
使用切平面
z
的方程创建函数句柄。
z = @(x,y) f(x0,y0) + fx0*(x-x0) + fy0*(y-y0);
绘制原始函数
f
(
x
,
y
)
、点
P
,以及在
P
位置与函数相切的平面
z
的片段。
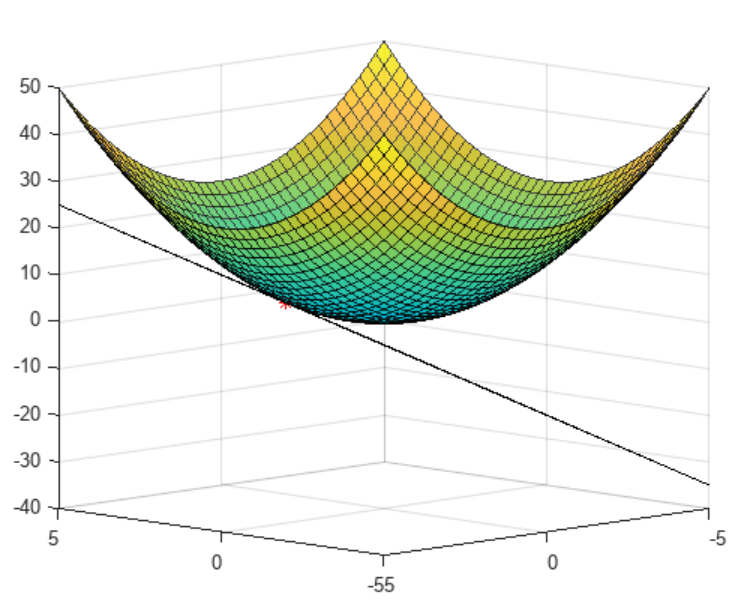
surf(xx,yy,f(xx,yy),'EdgeAlpha',0.7,'FaceAlpha',0.9)
hold on
surf(xx,yy,z(xx,yy))
plot3(1,2,f(1,2),'r*')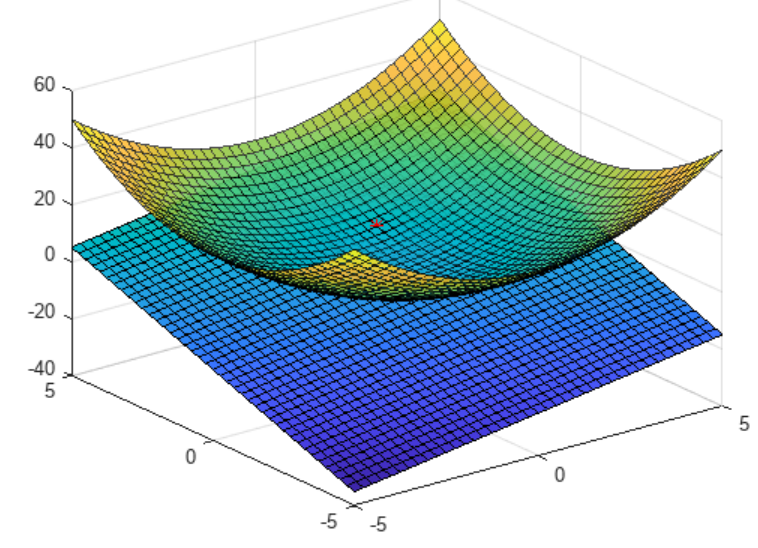
查看侧剖图。
view(-135,9)