注意:本文引用自专业人工智能社区Venus AI
更多AI知识请参考原站 ([www.aideeplearning.cn])
算法引言
蚁群算法,是一种模拟蚂蚁觅食行为的优化算法。想象一下,当你在野餐时,不小心洒了一些糖在地上。一只蚂蚁偶然发现了这些糖,就会在回巢的路上留下信息素,引导其他蚂蚁也找到这个食物来源。随着越来越多的蚂蚁走这条路,信息素会越来越浓,这条路就越来越“受欢迎”。但是,如果有一条更短的路径,那么蚂蚁会更快地来回运送食物,因此那条路径上的信息素会更快地积累,逐渐变成最优路径。这就是蚁群算法的灵感来源。
算法应用
蚁群算法的应用非常广泛,它可以用于解决旅行商问题(TSP)、车辆路径规划、网络路由优化等多种复杂的优化问题。由于其独特的优化机制和较好的寻优能力,蚁群算法在很多实际问题中都表现出了出色的性能。尤其在处理动态变化的问题时,蚁群算法能够有效地适应环境变化,找到新的最优解。
算法计算流程
蚁群算法 (Ant Colony Optimization, ACO) 是一种模拟蚂蚁受食行为的启发式算法,用于解决图形路径优化问题,蚁群算法基于蚂蚁在寻找食物源和返回巢穴时,通过分泌信息素来标记路径并指导其他蚂蚁的行为。这种信息素会随时间蒸发,而被更多蚂蚁使用的路径上的信息素会更浓,导致更多蚂蚁选择该路径。
初始化:
最开始,所有路径的信息素浓度 都被初始化为一个小的常数,这意味着一开始,所有路径都被视为同等可能。
构建解决方案:
蚂蚁们开始它们的搜索。每只蚂蚁根据信息素浓度和启发式信息(如路径长度的倒数) 来选择下一个地点。这是通过路径选择概率公式 实现的。蚂蚁选择路径的概率计算如下:
公式概述:
– 是在时间 t 蚂蚁从城市 i 移动到城市 j 的概率。
– 是路径 i 到 j 上的信息素浓度。
– 是启发式信息,如路径的倒数。
– α 和 β 分别控制信息素重要程度和启发式因子的相对重要程度。
– 分母是蚂蚁可以选择的所有路径上这些值的总和,用于归一化概率。
信息素浓度 :
– 信息素浓度是蚂蚁沟通找到好路径的方式。如果一条路径被很多蚂蚁选择,那么这条路径上的信息素浓度会增加,提示其他蚂蚁这可能是一个好的选择。
启发式信息 :
– 启发式信息通常是路径的逆长度(例如,两地点间距离的倒数)。路径越短,这个值就越大,表示路径越有可能是好的选择。
参数 α 和 β :
– α 调节信息素浓度的影响力。当 α 较大时,蚂蚁更可能遵循其他蚂蚁的路径。
– β 调节启发式信息 (如路径长度) 的影响力。当 β 较大时,蚂蚁更倾向于选择较短的路径。
为什么这样设计?
– 这个公式的设计反映了蚂蚁在自然界中寻找食物的行为。在自然界中,蚂蚁通过释放信息素和感应这些信息素来找到食物并传达信息。这个公式通过数学方式模仿了这一行为。
– 通过调整 α 和 β ,可以平衡蚂蚁在遵循其他蚂蚁的路径(即社会信息)和使用自己的启发式信息 (即个体认知) 之间的权衡。帮助蚂蚁决定下一步的最佳路径。这种设计旨在模拟蚂蚁在自然界中通过集体行为找到最优路径的方式,是一种有效的启发式搜索策略。通过在算法中调整参数 α 和 β,可以灵活地控制信息素浓度和启发式信息对蚂蚁行为的影响,从而适应不同类型的优化问题。
更新信息素
– 信息素更新公式:
其中,是时刻 t 在路径 i 到 j 上的信息素浓度, ρ 是信息素蒸发率,
是此时刻该路径上的信息素增量。
迭代过程
这个构建解决方案和更新信息素的过程会不断重复。每一次迭代,蚂蚁都会根据当前的信息素分布来做出决策,而信息素分布则是根据之前蚂蚁的经验不断更新的。
寻找最优解
经过多次迭代后,信息素浓度会在更优路径上积累,导致更多的蚂蚁选择这些路径。这个过程逐渐引导蚂蚁群体向最优解聚集。算法通常会在达到预定的迭代次数、找到满足特定质量的解决方案,或者在一定时间内没有显著改进后终止。
算法实例
这里演示使用蚁群优化算法解函数
1. 定义搜索空间:
– 假设 x 和 y 在 [−5,5] 的区间内。
2. 初始化:
– 放置2只蚂蚁:
– 蚂蚁1:
– 蚂蚁2:
– 初始化信息素浓度为一致值, 比如 1 。
3. 计算启发式信息:
– 对于蚂蚁 1,。
– 对于蚂蚁 2, 。
4. 选择下一步:
– 假设蚂蚁可以移动到相邻的整数坐标。为了简化,我们考虑蚂蚁1只有两个选项:移动到 (−4,2) 或 (−2,2) 。
– 假设 α=1 和 β=1 ,计算这两个选项的概率:
– 对于 (−4,2):
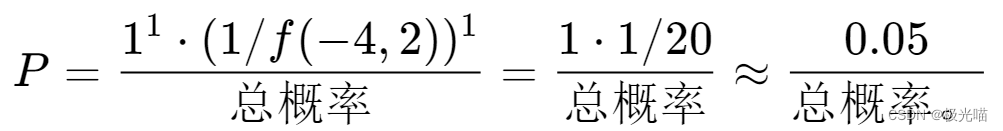
– 对于 (−2,2):
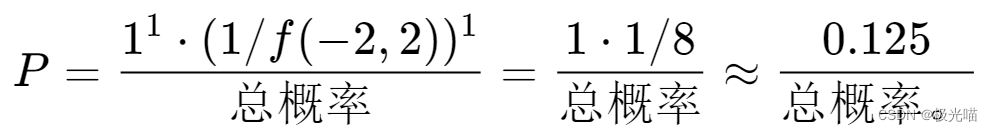
– 总概率 =0.05+0.125=0.175 。
– 因此,概率分别为 0.05/0.175≈0.286 和 0.125/0.175≈0.714 。
5. 移动蚂蚁:
– 假设蚂蚁1 随机选择了 (−2,2) (因为这个选项的概率更高)。蚂蚁2同样也进行选择。假设蚂蚁 2 选择移动到 (2,−1) 。
6. 计算新位置的函数值:
– 蚂蚁1在新位置的函数值: 。
– 蚂蚁2在新位置的函数值: 。
7. 更新信息素:
– 假设信息素蒸发率 ρ=0.1 。
– 新信息素浓度更新。例如,对于蚂蚁1经过的路径,更新为:
– ![]() 。
。
– ![]() 。
。
– ![]() 。
。
– 对蚂蚁 2 经过的路径进行类似的更新。
8. 重复过程:
– 如果需要,重复上述步骤,直到满足终止条件。
9. 输出最优解:
– 根据所有蚂蚁经过的路径和它们的函数值,选择最佳解。在这个例子中,蚂蚁 2 找到的位置 (2,−1) 有最小的函数值 5 。
10. 请注意,这个例子是一个简化的版本,实际应用中,ACO算法会涉及更多蚂蚁、更复杂的移动策略和信息素更新机制。这个例子旨在展示ACO的基本原理和计算步骤。在实际应用中,这个算法通常需要通过多次迭代来逐步改进解决方案。另外参数的设置也很重要,例如:
– 参数调整: α,β,ρ 的值会影响算法性能,需要根据具体问题调整。
– 信息素初始化:不宜过高,以避免早熟收敛。
– 停止条件:设置合理的迭代次数或解的质量阈值。
代码示例
为了实现上述例子的模拟,我们将使用Python语言。下面是蚁群算法的基本步骤:
- 放置蚂蚁:在蚁巢处放置一定数量的蚂蚁。
- 移动蚂蚁:蚂蚁根据信息素和启发式信息选择路径。
- 更新信息素:蚂蚁在走过的路径上留下信息素。
- 重复过程:重复上述步骤直到找到一个较优的路径。
让我们开始编写代码。
import numpy as np
import random
def f(x, y):
return x**2 + y**2
# 定义搜索空间
x_range = (-5, 5)
y_range = (-5, 5)
# 初始化参数
n_ants = 2 # 蚂蚁数量
alpha = 1 # 信息素重要程度的参数
beta = 1 # 启发式信息的参数
rho = 0.1 # 信息素蒸发率
iterations = 1 # 迭代次数
# 初始化蚂蚁位置
positions = [(random.uniform(*x_range), random.uniform(*y_range)) for _ in range(n_ants)]
# 初始化信息素浓度
pheromone = np.ones((11, 11)) # 信息素矩阵,考虑了-5到5的整数坐标
# 进行迭代
for iteration in range(iterations):
new_positions = []
for x, y in positions:
# 计算周围点的概率
probabilities = []
for dx in [-1, 0, 1]:
for dy in [-1, 0, 1]:
new_x, new_y = x + dx, y + dy
if new_x >= x_range[0] and new_x <= x_range[1] and new_y >= y_range[0] and new_y <= y_range[1]:
tau = pheromone[int(new_x - x_range[0])][int(new_y - y_range[0])]
eta = 1 / f(new_x, new_y) if f(new_x, new_y) != 0 else 1
p = (tau ** alpha) * (eta ** beta)
probabilities.append((p, (new_x, new_y)))
# 选择新位置
total_p = sum([p[0] for p in probabilities])
probabilities = [(p[0]/total_p, p[1]) for p in probabilities]
new_position = random.choices([p[1] for p in probabilities], weights=[p[0] for p in probabilities], k=1)[0]
new_positions.append(new_position)
# 更新信息素
pheromone[int(x - x_range[0])][int(y - y_range[0])] *= (1 - rho)
pheromone[int(x - x_range[0])][int(y - y_range[0])] += 1 / f(*new_position)
positions = new_positions
# 找到并输出最优解
best_position = min(positions, key=lambda pos: f(*pos))
best_value = f(*best_position)
best_position, best_value可视化蚁群算法的效果如下:
![图片[1]-蚁群优化算法(Ant Colony Optimization Algorithm)-VenusAI](https://img-blog.csdnimg.cn/img_convert/9702f5a74b8f906d0a93badcfcf79ece.png)
现在我们已经成功地可视化了蚁群算法找到的最短路径。在两个子图中,您可以看到蚁群优化算法的初始状态(左图)和训练完成后的状态(右图),以及它们相对于函数表面的位置。这个可视化展示了蚂蚁是如何从初始位置移动到新位置的,并且可以看到它们在函数表面上的相对高度变化。