文章目录
- 一、代码debug
- 二、原理
本文主要参考了CSDN上的 另一篇文章,但规范了公式的推导过程和修缮了部分代码
一、代码debug
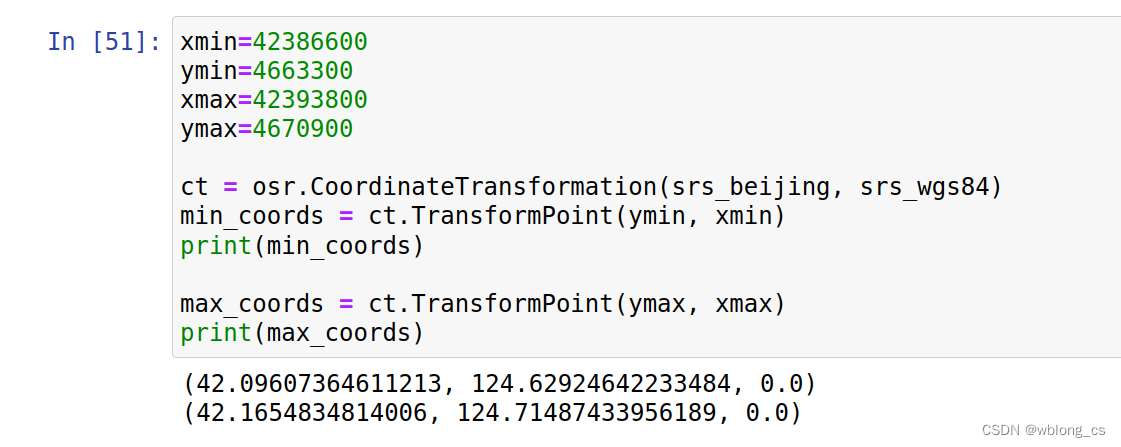
首先,我们将所有的代码放到MATLAB中,很快在命令行中出现了错误信息

很显然有问题,但是我不知道发生了什么问题。我猜测可能是求解器没有正确安装,因此我正确安装了Gurobi求解器

注意安装Gurobi求解器需要验证license,具体内容可以查询网络上的安装教程。在命令行中输入grbgetkey+licence 就可以完成激活。

但此时还是有问题,我经过查询得知是MEX文件无法指定,是系统路径没有添加gurobi文件的bin,因此我添加到系统路径中


此后文件便可以正确运行了,结果如下。


二、原理
现考虑如下非凸二次规划问题
min f ( x , y ) = [ x , y ] Q [ x , y ] T = x 2 + x y − y 2 s.t. − 1 ≤ x ≤ 1 − 1 ≤ y ≤ 1 \begin{aligned} &\operatorname*{min}f(x,y)&& \left.=\left[\begin{matrix}{x,y}\\\end{matrix}\right.\right]Q\left[\begin{matrix}{x,y}\\\end{matrix}\right]^{T} \\ &&&=x^{2}+xy-y^{2} \\ &\text{s.t.}&& -1\leq x\leq1 \\ &&&-1\leq y\leq1 \end{aligned} minf(x,y)s.t.=[x,y]Q[x,y]T=x2+xy−y2−1≤x≤1−1≤y≤1
其中,
Q = [ 1 0.5 0 5 ] . Q=\begin{bmatrix}1&0.5\\0&5\\\end{bmatrix}. Q=[100.55].
原问题的目标函数可以通过特征值分解转化为凸函数减去凸函数的形式,凸函数减去凸函数未必是凸函数。
Q = V D V T = V ( λ P − λ N ) V T = V λ P V T ⏟ P − V λ N V T ⏟ N \begin{aligned}Q=VDV^T=V\left(\lambda_P-\lambda_N\right)V^T=\underbrace{V\lambda_PV^T}_{P}-\underbrace{V\lambda_NV^T}_{N}\end{aligned} Q=VDVT=V(λP−λN)VT=P VλPVT−N VλNVT
其中,矩阵 P P P 和 N N N 都是半正定矩阵,矩阵 D D D 的表达式如下
D = [ λ 1 λ 2 ⋱ λ k λ k + 1 ⋱ ] = [ λ 1 λ 2 ⋱ λ k 0 ⋱ ] ⏟ λ P − [ 0 0 ⋱ 0 − λ k + 1 ⋱ ] ⏟ λ N D=\left.\left[\begin{array}{cccc}\lambda_{1}& & & & & \\ &\lambda_{2}& & & &\\ & & \ddots & & &\\ & & & \lambda_{k}& &\\ & & & & \lambda_{k+1} &\\ & & & & &\ddots \end{array}\right.\right] =\underbrace{\left.\left[\begin{array}{cccc}\lambda_{1}& & & & & \\ &\lambda_{2}& & & &\\ & & \ddots & & &\\ & & & \lambda_{k}& &\\ & & & & 0 &\\ & & & & &\ddots \end{array}\right.\right]}_{\lambda_P} -\underbrace{\left.\left[\begin{array}{cccc}0& & & & & \\ &0 & & & &\\ & & \ddots & & &\\ & & &0& &\\ & & & & - \lambda_{k+1} &\\ & & & & &\ddots \end{array}\right.\right]}_{\lambda_N} D= λ1λ2⋱λkλk+1⋱ =λP λ1λ2⋱λk0⋱ −λN 00⋱0−λk+1⋱
其中 λ 1 , λ 2 , … , λ k ≥ 0 , λ k + 1 , λ k + 2 , … < 0 \lambda_1,\lambda_2,\ldots,\lambda_k\geq0,\lambda_{k+1},\lambda_{k+2},\ldots<0 λ1,λ2,…,λk≥0,λk+1,λk+2,…<0。
对目标函数的第二项 [ x , y ] N [ x , y ] T \left[x,y\right]N[x,y]^T [x,y]N[x,y]T 在点 ( x ∗ , y ∗ ) (x^{*},y^{*}) (x∗,y∗) 处进行凸近似,即在点 ( x ∗ , y ∗ ) (x^{*},y^{*}) (x∗,y∗) 处进行一阶泰勒展开
− [ x ∗ , y ∗ ] N [ x ∗ , y ∗ ] T − [ ∇ ( [ x , y ] N [ x , y ] T ) ∣ x ∗ , y ∗ ] T ( [ x , y ] − [ x ∗ , y ∗ ] ) T = − [ x ∗ , y ∗ ] N [ x ∗ , y ∗ ] T − ( 2 N [ x ∗ , y ∗ ] T ) T ( [ x , y ] − [ x ∗ , y ∗ ] ) T = − 2 [ x ∗ , y ∗ ] N [ x , y ] T + [ x ∗ , y ∗ ] N [ x ∗ , y ∗ ] T \begin{aligned}&-\left[x^*,y^*\right]N\left[x^*,y^*\right]^T-\left[\nabla\left(\left[x,y\right]N\big[x,y\big]^T\right)\right|_{x^*,y^*}\Big]^T\left(\left[x,y\right]-\left[x^*,y^*\right]\right)^T\\ &=-\left[x^*,y^*\right] N \left[x^*,y^*\right]^T -\left(2N\left[x^*,y^*\right]^T\right)^T\left(\left[x,y\right]-\left[x^*,y^*\right]\right)^T\\ &=-2{\Big[}x^{*},y^{*}{\Big]}N{\Big[}x,y{\Big]}^{T}+{\Big[}x^{*},y^{*}{\Big]}N{\Big[}x^{*},y^{*}{\Big]}^{T} \end{aligned} −[x∗,y∗]N[x∗,y∗]T−[∇([x,y]N[x,y]T) x∗,y∗]T([x,y]−[x∗,y∗])T=−[x∗,y∗]N[x∗,y∗]T−(2N[x∗,y∗]T)T([x,y]−[x∗,y∗])T=−2[x∗,y∗]N[x,y]T+[x∗,y∗]N[x∗,y∗]T
至此,原问题可转化为:
min
f
(
x
,
y
)
=
[
x
,
y
]
P
[
x
,
y
]
T
−
2
[
x
∗
,
y
∗
]
N
[
x
,
y
]
T
+
[
x
∗
,
y
∗
]
N
[
x
∗
,
y
∗
]
T
s
.
t
.
−
1
≤
x
≤
1
−
1
≤
y
≤
1
\begin{aligned} &\min & &f\left(x,y\right)=\left[x,y\right]P\left[x,y\right]^{T}-2\left[x^{*},y^{*}\right]N\left[x,y\right]^{T}+\left[x^{*},y^{*}\right]N\left[x^{*},y^{*}\right]^{T} \\ &s.t.& &-1\leq x\leq1 \\ & & &-1\leq y\leq1 \end{aligned}
mins.t.f(x,y)=[x,y]P[x,y]T−2[x∗,y∗]N[x,y]T+[x∗,y∗]N[x∗,y∗]T−1≤x≤1−1≤y≤1
clear all
close all
clc
Q=[1,0.5;0.5,-1];
x=sdpvar(2,1);
xmin=-1;
xmax=1;
Constraints=[];
Constraints=[Constraints,xmin<=x<=xmax];
ops = sdpsettings('solver', 'gurobi', 'verbose', 0);
[V,D] = eig(Q);%计算A的特征值对角阵D和特征向量V,使AV=VD成立
lambda_P=D;
lambda_N=-D;
lambda_P(find(D<0))=0;
lambda_N(find(D>0))=0;
P=V*lambda_P*V';
N=V*lambda_N*V';
x0=[0.5;0.5];
x_temp=x0;
while(1)
f_k=(x'*P*x-2*x_temp'*N*x+x_temp'*N*x_temp);
sol=solvesdp(Constraints,f_k,ops);
display([sol.info,' 目标函数值:',num2str(value(x_temp'*Q*x_temp))])
x_temp_before=x_temp;
x_temp=value(x);
if sqrt(sum((x_temp-x_temp_before).^2)/length(x_temp))<1e-10
break
end
end
x_result=x_temp
X = gridsamp([-1 -1;1 1], 40);
[m,~]=size(X);
YX=zeros(m,1);
for i=1:size(X,1)
x=X(i,:);
y=x*Q*x';
YX(i)=y;
end
X1 = reshape(X(:,1),40,40); X2 = reshape(X(:,2),40,40);
YX = reshape(YX, size(X1));
figure(1), mesh(X1, X2, YX)%绘制预测表面
hold on
scatter3(x_temp(1),x_temp(2),x_temp'*Q*x_temp,200,'r','pentagram','filled')





![[羊城杯 2020]Easyphp2 ---不会编程的崽](https://img-blog.csdnimg.cn/direct/aba84cbd418d4d6594ce30c648ce9029.png)